数学部分摘要
主要内容:1.素数 2.同余 3.组合数学 4.矩阵乘法
1.素数
试除法
试除法可以对任意位置的正整数进行查询,除了试除法以外,还有其他的优秀的算法也可以对单个数进行判定,如 Miller_Rabin
试除法在单个查询时,可以以 \(O(\sqrt{n})\) 的时间内判定一个数是否是质数,一般而言,试除法已经能够满足大部分题目对于质数查找的需求
质数筛
问题:给定一个整数 N ,求出 1~N 之间的所有质数,称为质数筛
1.Eratosthenes筛法(埃氏筛)
该算法基于一个思想:对于一个数 x ,它的所有倍数 \(2x , 3x , …… , dx\) , 均为合数,显然,该命题成立
由此,埃氏筛对所有未被标记过的数进行筛选,经它的所有倍数筛去,剩余的数即为素数
但是, 2 和 3 均为质数,未被标记,它的倍数 6 会被标记多次,对复杂度有一定的影响,\(O(N\log{\log{N}})\)
2.线性筛
线性筛通过“从大到小积累质因子”的方法标记每一个合数,这样,对于一个合数,就可以避免过多的冗余运算
int v[maxn],prime[maxn];
void primes(int n)
{
memset(v,0,sizeof(v));//最小质因子
m=0;//质数个数
for(int i=2;i<=n;i++)
{
if(!v[i])//未被标记,i为质数
{
v[i]=i;
prime[++m]=i;
}
for(int j=1;j<=m;j++)
{
if(prime[j]>v[i]||prime[j]>n/i) break;//i有更小的质因子,或者超出n的范围
v[i*prime[j]]=prime[j];//prime[j]为合数 i*prime[j]的最小质因子
}
}
}
欧拉函数
- 定义:欧拉函数 \(\varphi(n)\) 表示在小于 n 的数中,与 n 互质的数的个数
- 计算公式:\(\varphi(n)\) = \(n \times \prod_{i=1}^{k}{(1-\frac{1}{p_i})}\)
- 性质:欧拉函数为积性函数(积性函数定义:若任意的两个互质的正整数满足\(f(xy)=f(x)\times f(y)\),则称函数 \(f(x)\) 为积性函数)
- 性质:\(\sum_{d|n}{\varphi(d)} = n\)
2.同余
定义 & 定理
- 定义:若整数 a , b 除以正整数 m 的余数相等,则称 a , b 模 m 同余,记为:\(a \equiv b (\bmod m)\)
- 定义:乘法逆元:若整数 b , m 互质,则必然存在 \(a\times b \equiv 1 (\bmod m)\) ,则称 a 为 b 的乘法逆元
- 费马小定理:若 p 为质数 , 则对于任意整数 a , 有 \(a^p \equiv a (\bmod p)\)
- 欧拉定理: 若正整数 a , n 互质,则 \(a^{\varphi(n)} \equiv 1 (\bmod n)\)
扩展欧几里得算法(exgcd)
- 贝祖定理:对于任意的整数 a,b,存在一对整数 x,y,满足 \(ax+by = gcd(a,b)\)
利用贝祖定理,即可得到上式中整数 x,y 的计算方法,称为扩展欧几里得算法
int exgcd(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1,y=0;
return a;
}
int d=exgcd(b,a&b,x,y);//利用扩展欧几里得算法,可顺便求得 a 与 b 的最大公约数
int z=x;
x=y;
y=z-(a/b)*y;
return d;
}
利用扩展欧几里得算法,即可求得不定方程 \(ax + by = gcd(a,b)\) 的一组特解,则其通解可表示为:\(x = \frac{c}{d}x_0 + k\frac{b}{d}\) , \(y = \frac{c}{d}y_0 - k\frac{a}{d}\)
中国剩余定理(crt)
- 设 \(m_1 , m_2 , …… , m_n\) 为两两互质的正整数,\(m = \prod_{i=1}^{n}{m_i}\) , \(M_i = m/m_i\) , \(t_i\) 是线性同余方程 \(M_i t_i \equiv 1 (\bmod m_i)\) 的一个解,
则对于任意的 n 个整数 \(a_1 , a_2 , …… , a_n\) , 方程组:
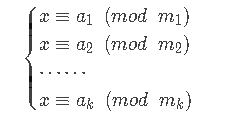
有整数解,解为: \(x = \sum_{i=1}^{n}{a_iM_it_i}\)
证明略
3.组合数学
组合数学向来是数学上的一大难点,但是应用性极强,可以帮助解决许多复杂的问题,与容斥原理配合食用效果更佳 (建议百度搜索:小葱同学)
加法原理
- 若完成一件事的方法有 n 类,其中第 i 类方法包括 \(a_i\) 种不同的方法,且这些方法互不重合,则完成这件事共有:\(a_1+a_2+a_3+……+a_n\) 种方法
乘法原理
- 若完成一件事的需要有 n 步,其中完成第 i 步包含 \(a_i\) 种不同的方法,且这些步骤互不干扰,则完成这件事共有:\(a_1\times a_2\times a_3 \times …… \times a_n\) 种方法
排列数
- 从 n 个不同元素中依次取出 m 个元素排成一列,产生的不同排列的数量为:\(A_n^m = \frac{n!}{(n-m)!}\)
组合数
- 从 n 个不同元素中取出 m 个元素组成一个集合,产生的不同集合的数量为:\(C_n^m = \frac{n!}{(n-m)!(m)!}\)
性质
1.\(C_n^m = C_n^{n-m}\)
2.\(C_n^m = C_{n-1}^m + C_{n-1}^{m-1}\)
3.\(C_n^0 + C_n^1 + C_n^2 + …… + C_n^n = 2^n\)
4.\((a+b)^n = \sum_{k=0}^{n}{C_{n}^{k}{a^k}{b^{n-k}}}\) (二项式定理)
Lucas 定理
公式:\(C_n^m \equiv C_{n \ mod \ p}^{m \ mod \ p} * C_{n/p}^{m/p} \ (\bmod p)\)
(证明略)

