洛谷 P2822 组合数问题
P2822 组合数问题(来自小破谷的第一道绿题)
题目描述

输入格式
第一行有两个整数 t,kt,k,其中 tt 代表该测试点总共有多少组测试数据,kk 的意义见问题描述。
接下来 tt 行每行两个整数 n,mn,m,其中 n,mn,m 的意义见问题描述。
输出格式
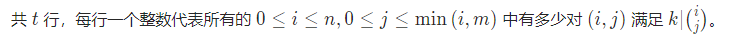
说明/提示
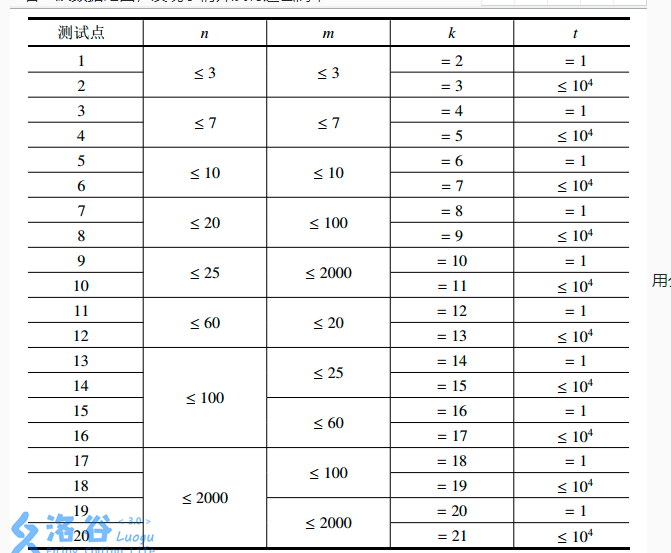
我们知道,在二项式定理中,每一项的二项式系数都相应的对应着杨辉三角的某一行
如图:
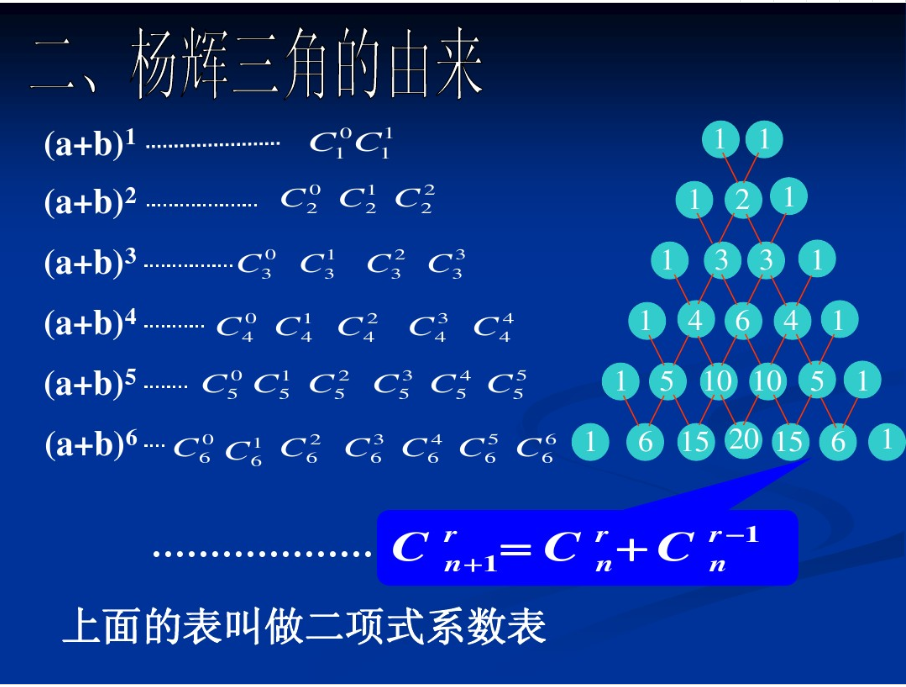
本题的测试点只在2000的范围内,所以可以打表,将2000以内的排列数全部求出来。
之后如果用二次遍历来排查能不能整除,复杂度会比较大,会有可能爆时间(事实上也爆时间了),只能得90分,
但是,可以用求前缀和来简化,

本题的前缀和公式也相应地是:s[x][y]=b[x-1][y]+b[x][y-1]-b[x-1][y-1] ;

在这道题中,要求红色三角形右下方的元素的前缀和,就是整个红色三角形所包含的元素的加和
而这个红色部分的左侧元素有一前缀和为黄色三角形所示部分,其上面的元素亦有前缀和为绿色三角形
再加上此元素本身,就可构成一个整体的前缀和,但是,在绿色三角形和黄色三角形的部分,所表示的三角形前缀和
有一定的重叠部分,这个部分需要减去,那么这个前缀和即为紫色三角形,即为sum[i-1][j-1]的前缀和
固有此公式:s[x][y]=b[x-1][y]+b[x][y-1]-b[x-1][y-1] ;
代码如下:
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<math.h> using namespace std; int k,a[5000][5000]; int s[5000][5000]; void st(int k) { a[1][1]=1;//设置初始状态 for(int i=1;i<=2000;i++) { a[i][0]=1; } for(int i=2;i<=2000;i++) { for(int j=1;j<=i;j++) { a[i][j]=(a[i-1][j-1]%k+a[i-1][j]%k)%k;//杨辉三角的求和公式,记得模k,以防爆炸QAQ } } for(int i=2;i<=2000;i++) { for(int j=1;j<=i;j++) { s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1];//求杨辉三角的每一项符合条件的前缀和 if(a[i][j]==0) { s[i][j]++;//计算元素本身 } } s[i][i+1]=s[i][i];//当元素在左右两侧时,该元素的值为1,那么必然没有它自己,同时,他的前缀和的上方元素也是1,也就是说,他的前缀和就是它的前一位元素的前缀和 } } int main(void) { int t,k; cin>>t>>k; st(k); while(t--) { int n,m; cin>>n>>m; if(m>n) cout<<s[n][n]<<endl; else cout<<s[n][m]<<endl; } return 0; }
这里相应的,只要输出s[n][m],即输出前缀和,即可得到正确答案。
这里的优化,最关键的就是这里的前缀和求值,重在理解!!!
可以理解为:
用局部面积之和,再加上自己,减去重复的地方,即得前缀和。
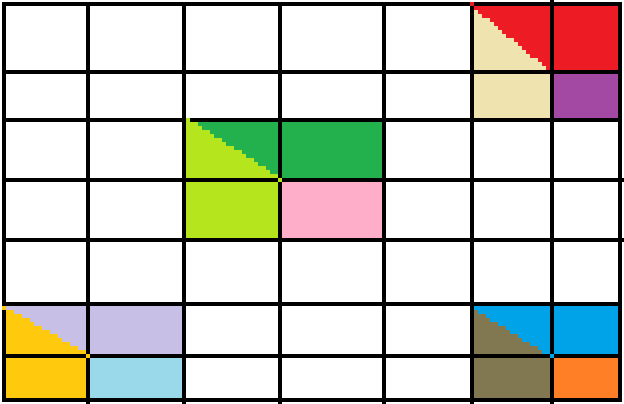
这里,每一部分上色的区域中,右下角的矩形即为当前要求的前缀和,他可以由另外的三部分上色的矩形得到,但是在计算的时候会算重一次,双色的矩形,故应减去

