洛谷题单指南-最短路-P4779 【模板】单源最短路径(标准版)
原题链接:https://www.luogu.com.cn/problem/P4779
题意解读:单源最短路算法。
解题思路:
一、Dijikstra算法,适用于没有负权边的单源最短路场景
1、Dijikstra-朴素版
算法思想:用已经确定最短路的点去更新与其相连的没有确定最短路的点
- 初始化每个点到起点的距离dist[i] = INF,dist[s] = 0,s是起点
- 每次在没有确定最短路的点中找距离起点最近的点u
- 将u标记为已经确定了最短路vis[u] = true
- 用u去更新与u相连的其他点的最短路,这一步称为松弛操作,具体为:设有一个邻接点v,如果dist[v] > dist[u] + w[v],则dist[v] = dist[u] + w[v]
- 重复n次以上三步
样例模拟:
- 初始时
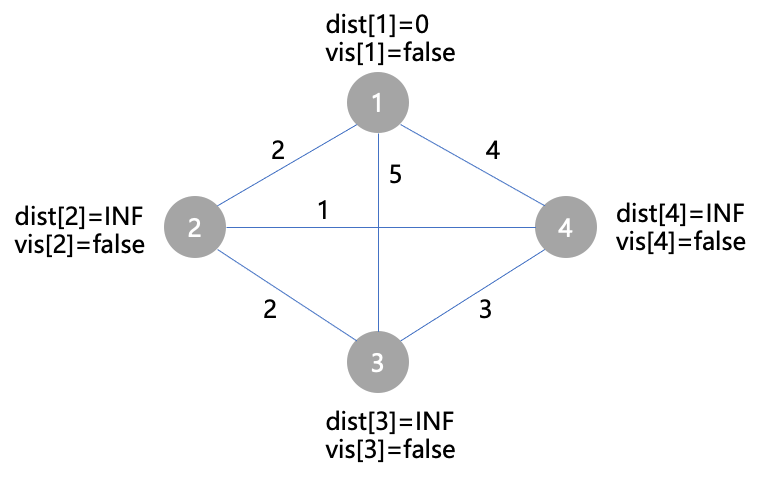
- 第一次找未标记的距离起点最近的点1,先标记,再用点1对2/3/4进行松弛操作
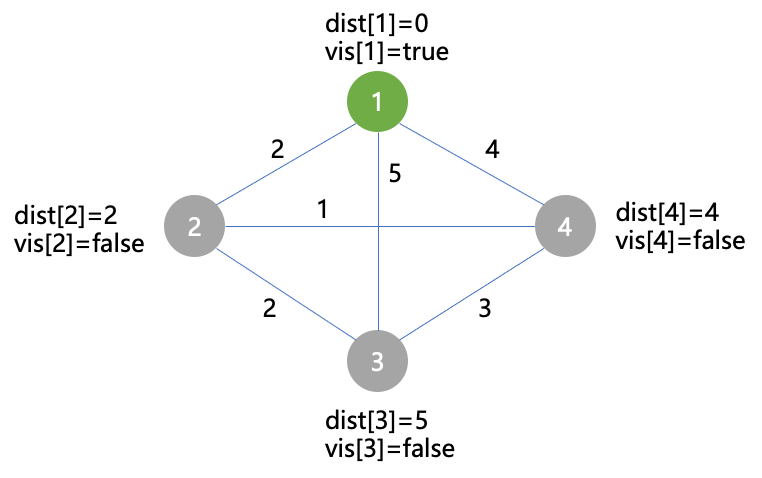
- 第二次找未标记的距离起点最近的点2,先标记,再用点2对3/4进行松弛操作

- 第三次找未标记的距离起点最近的点4,先标记,再用点4对3进行松弛操作
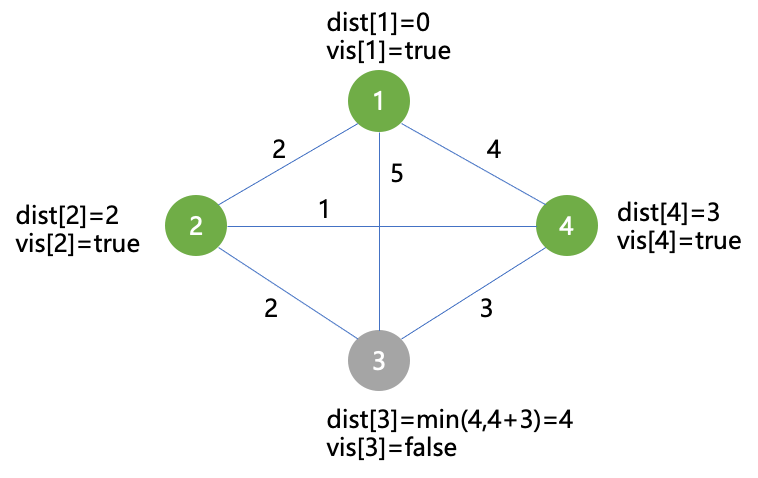
- 第四次找未标记的距离起点最近的点3,标记,结束

1到各个点最短距离为:0 2 4 3
时间复杂度:O(n^2),适用于稠密图
代码示例:无法通过此题,但可以通过https://www.luogu.com.cn/problem/P3371
#include <bits/stdc++.h>
using namespace std;
const int N = 500005;
int h[N], e[N], w[N], ne[N], idx;
int dist[N];
bool vis[N];
int n, m, s;
void add(int a, int b, int c)
{
e[++idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
}
void dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[s] = 0;
for(int i = 1; i <= n; i++)
{
int u = 0;
for(int j = 1; j <= n; j++)
{
if(!vis[j] && dist[j] < dist[u]) u = j;
}
vis[u] = true;
for(int j = h[u]; j != -1; j = ne[j])
{
int v = e[j];
dist[v] = min(dist[v], dist[u] + w[j]);
}
}
}
int main()
{
memset(h, -1, sizeof(h));
cin >> n >> m >> s;
for(int i = 1; i <= m; i++)
{
int u, v, w;
cin >> u >> v >> w;
add(u, v, w);
}
dijkstra();
for(int i = 1; i <= n; i++)
{
if(dist[i] == 0x3f3f3f3f) cout << INT_MAX << " ";
else cout << dist[i] << " ";
}
return 0;
}2、Dijikstra-堆优化版
在朴素版算法中,每次都找到未标记过的离起点最近的点,通过该点进行松弛操作,这一步枚举复杂度是O(n),既然要每次找未标记过的距离最小的点,可以借助于堆。
堆中元素需包括两个信息:与起点的距离、节点编号,且必须是小根堆,因此可以这样定义:
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>> > pq;
优化过程:
- 初始时,将起点距离和编号{0,s}加入堆
- 每次取堆顶元素,如果标记过则跳过,否则标记,再用堆顶元素的节点进行松弛操作,并将邻点加入堆,直到堆为空
时间复杂度:O(mlogn),适用于稀疏图
100分代码:
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 200005;
int h[N], e[N], w[N], ne[N], idx;
int dist[N];
bool vis[N];
int n, m, s;
void add(int a, int b, int c)
{
e[++idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
}
void dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[s] = 0;
priority_queue<PII, vector<PII>, greater<PII>> pq;
pq.push({0, s});
while(pq.size())
{
PII p = pq.top(); pq.pop();
int u = p.second;
if(vis[u]) continue;
vis[u] = true;
for(int j = h[u]; j != -1; j = ne[j])
{
int v = e[j];
if(dist[u] + w[j] < dist[v])
{
dist[v] = dist[u] + w[j];
pq.push({dist[v], v});
}
}
}
}
int main()
{
memset(h, -1, sizeof(h));
cin >> n >> m >> s;
for(int i = 1; i <= m; i++)
{
int u, v, w;
cin >> u >> v >> w;
add(u, v, w);
}
dijkstra();
for(int i = 1; i <= n; i++) cout << dist[i] << " ";
return 0;
}二、SPFA算法,适用于用负权边的单源最短路场景
1、Bellman Ford算法
核心思想:重复n轮,每次对m条边进行松弛操作,对边a->b权值w进行松弛操作即dist[b] = min(dist[b], dist[a] + w)。
每1轮重复,如果进行了松弛操作更新dist,说明起点到该点的最短路上边数加1,
当第n轮还能进行松弛操作时,说明最短路边长达到n,点数为n+1,但是一共只有n个点,因此必存在负权回路。
需要注意的是,每一轮对m条边进行松弛操作前,需要备份dist数组到back,更新时用备back进行更新:dist[b] = min(dist[b], back[a]+w)。
时间复杂度:稳定为O(nm)
适用场景:限制边数的最短路问题
2、SPFA算法
SPFA在Bellman Ford算法基础上进行优化,由于Bellman Ford算法每轮松弛操作要对m条边都处理一遍,对于那些最短路不会更新的点其实没有必要。
那么,哪些点是有可能更新最短路的呢?显然,就是上一次更新过最短路的点的邻接点!因为有点的最短路更新,才可能导致邻接点的最短路也更新。
算法过程:
- 通过队列保存要进行松弛操作的点
- 每次出队,标记节点已出队
- 对节点所有邻接点进行松弛操作,如果进行了松弛操作且该领接点当前不在队列,就加入队列,并标记已加入队列
- 直到队列为空
时间复杂度:通常情况O(n),最坏情况为O(nm),是可能通过构造特殊数据卡掉的
适用场景:存在负权边的最短路问题,主要用于判断负环
本题用SPFA只能得到部分分!
32分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 200005;
int h[N], e[N], w[N], ne[N], idx;
int dist[N];
bool vis[N];
int n, m, s;
void add(int a, int b, int c)
{
e[++idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
}
void spfa()
{
memset(dist, 0x3f, sizeof(dist));
dist[s] = 0;
queue<int> q;
q.push(s);
vis[s] = true;
while(q.size())
{
int u = q.front(); q.pop();
vis[u] = false; //标记已出队
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(dist[u] + w[i] < dist[v])
{
dist[v] = dist[u] + w[i];
if(!vis[v]) //不在队列里才加入
{
q.push(v);
vis[v] = true;
}
}
}
}
}
int main()
{
memset(h, -1, sizeof(h));
cin >> n >> m >> s;
for(int i = 1; i <= m; i++)
{
int u, v, w;
cin >> u >> v >> w;
add(u, v, w);
}
spfa();
for(int i = 1; i <= n; i++) cout << dist[i] << " ";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号