洛谷题单指南-线段树的进阶用法-P3834 【模板】可持久化线段树 2
原题链接:https://www.luogu.com.cn/problem/P3834
题意解读:静态区间第k小问题,可持久化线段树(也称为主席树)模版题。
解题思路:
一、朴素想法:如何求完整区间[1,n]第k小
1、权值线段树
设n个数构成序列a,b数组代表a中元素出现的次数,即b数组的构建方式为对每一个a[i]做b[a[i]]++。
针对b数组区间构建的线段树,称为权值线段树,权值线段树的节点维护的信息是节点范围内所有元素出现的次数。
因此,可以说,普通线段树节点表示的区间是下标,权值线段树节点表示的区间是值域。
2、权值线段树主要操作
节点定义:
struct Node
{
int l, r; //l,r对应原数组a的值
int cnt; //[l, r]的数出现的个数
} tr[N * 4];单点修改:
//将数值x的个数增加v,也就是将节点x维护的cnt加v
void update(int u, int x, int v)
{
if(tr[u].l == tr[u].r) tr[u].cnt += v;
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) update(u << 1, x, v);
else update(u << 1 | 1, x, v);
pushup(u);
}
}区间查询:
//查询[l,r]范围所有值出现的次数
int query(int u, int l, int r)
{
if(tr[u].l >= l && tr[u].r <= r) return tr[u].cnt;
else if(tr[u].l > r || tr[u].r < l) return 0;
else return query(u << 1, l, r) + query(u << 1 | 1, l, r);
}为了演示权值线段树的基本操作,这里给出求逆序对问题(P1908)的权值线段树解法:
a、对序列a[]每一个元素进行离散化处理
b、依次遍历每一个元素a[i],在区间[a[i] + 1, n]中查询所有元素个数,累加到答案
c、对a[i]个数进行加1,update(1, a[i], 1)
注意:[a[i] + 1, n]的元素个数意味着排在a[i]前面且值比a[i]大的元素个数,也就是逆序对!
下面是完整代码:
P1908-权值线段树做法
#include <bits/stdc++.h>
using namespace std;
const int N = 500005;
struct Node
{
int l, r; //l,r对应原数组a的值
int cnt; //[l, r]的数出现的个数
} tr[N * 4];
int a[N];
vector<int> b;
int n;
long long ans;
//查询离散化后的值
int find(int x)
{
return lower_bound(b.begin(), b.end(), x) - b.begin() + 1;
}
void pushup(int u)
{
tr[u].cnt = tr[u << 1].cnt + tr[u << 1 | 1].cnt;
}
void build(int u, int l, int r)
{
tr[u] = {l, r};
if(l == r) tr[u].cnt = 0;
else
{
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
//将数值x的个数增加v,也就是将节点x维护的cnt加v
void update(int u, int x, int v)
{
if(tr[u].l == tr[u].r) tr[u].cnt += v;
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) update(u << 1, x, v);
else update(u << 1 | 1, x, v);
pushup(u);
}
}
//查询[l,r]范围所有值出现的次数
int query(int u, int l, int r)
{
if(tr[u].l >= l && tr[u].r <= r) return tr[u].cnt;
else if(tr[u].l > r || tr[u].r < l) return 0;
else return query(u << 1, l, r) + query(u << 1 | 1, l, r);
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
b.push_back(a[i]);
}
sort(b.begin(), b.end()); //排序
b.erase(unique(b.begin(), b.end()), b.end()); //去重
build(1, 1, b.size()); //建立线段树
for(int i = 1; i <= n; i++)
{
int x = find(a[i]); //离散化
ans += query(1, x + 1, b.size()); //查询在a[i]前面出现且比a[i]大的元素个数
update(1, x, 1); //将a[i]出现的次数加1
}
cout << ans;
return 0;
}3、查询第k小
除了查询元素个数,权值线段树也可以查询第k小,
由于权值线段树叶节点表示的就是值的个数,而且叶节点从分布上从左到右是递增的,
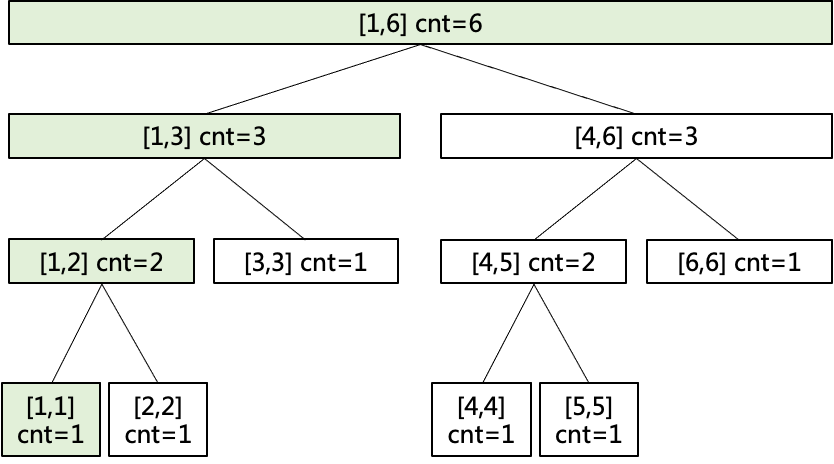
如序列5 4 2 6 3 1生成的权值线段树为左图所示:
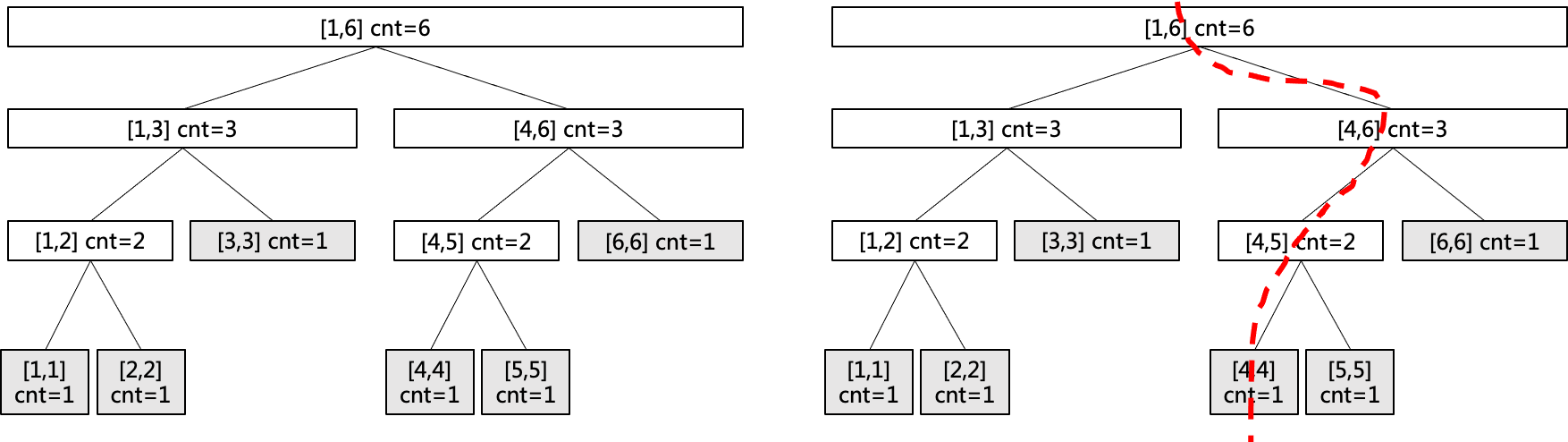
要查询第4小元素,查询路径如右图所示,主要逻辑如下:
从根节点[1,6]开始,先看左子树元素个数为3, 4 > 3,因此要找的元素在右子树,转化成在右子树查第4 - 3 = 1个元素;
再看[4,6]节点,其左子树元素个数为2, 2 > 1,因此要找的元素在左子树;
再看[4,5]节点,其左子树元素个数为1, 1 >= 1,因此要找的元素在左子树;
再看[4,4],已经到叶子结点,所以要找的第4小元素就是4。
以上过程用代码描述为
//查询第k小的元素
int find_kth(int u, int k)
{
if(tr[u].l == tr[u].r) return tr[u].l; //到了叶子节点说明找到了第k小元素
else
{
int leftcnt = tr[u << 1].cnt; //左子树所有元素个数
if(leftcnt >= k) return find_kth(u << 1, k); //如果左子树元素个数>k,说明第k小在左子树
else return find_kth(u << 1 | 1, k - leftcnt); //否则在右子树去找第k - leftcnt小
}
}如此,权值线段树就可以解决查询完整区间第k小问题。
二、进阶思考:如何求指定区间[l,r]第k小
1、权值线段树的可加/减性
针对序列5 4 2 6 3 1,我们采用逐步建立线段树的方式:
建立初始线段树:

对序列5建立线段树:
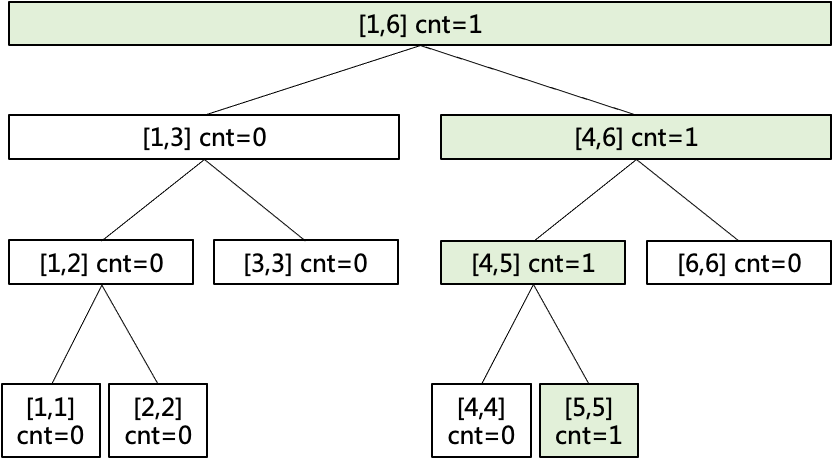
对序列5 4建立线段树:

对序列5 4 2建立线段树:
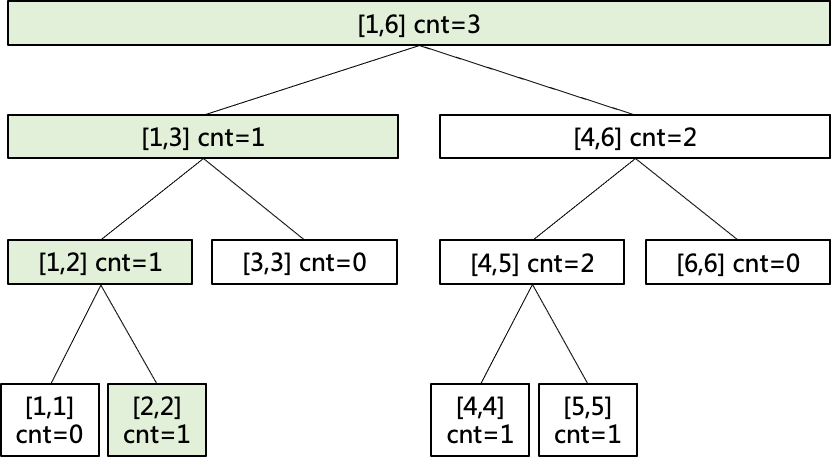
对序列5 4 2 6建立线段树:

对序列5 4 2 6 3建立线段树:
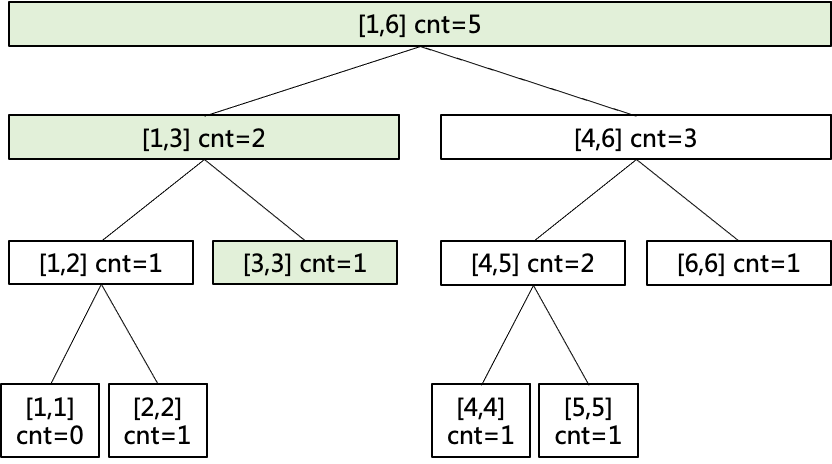
对序列5 4 2 6 3 1建立线段树:
不难发现,序列每增加一个值,线段的变化都是在前一个线段树基础上将值到根节点一条路径上的cnt都加1,因此说权值线段树具有可加性。
2、前缀和思想
根据以上可加性的分析,可以知道对于值区间a[1] ~ a[i]建立的线段树可以维护a[1] ~ a[i]的元素个数
那么如何才能知道一个区间a[l] ~ a[r]各个元素的个数呢?这里可以借助前缀和的思想,也就是用a[1] ~ a[r]的线段树减去a[1] ~ a[l-1]的对应各个节点的cnt值,就可以得到l ~ r区间范围各个元素值的个数。
例如,用序列5 4 2 6 3 1的线段树 减去 序列5 4的线段树对应节点值,就得到了序列2 6 3 1的线段树:

这样一来,我们可以考虑针对所有的a[1] ~ a[i] ( 1<=i<=n) 都建立一棵线段树,算上初始空线段树,一共是n + 1棵线段树,
要查询区间[l, r]第k小,可以用第r棵线段树减去第l-1棵线段树对应节点的cnt,然后利用上述介绍的查询第k小的算法即可得到区间k小值。
3、可持久化
如果要完整的建立n + 1棵线段树,空间复杂度将达到 O(n2*4)级别,不可接受,就需要借助于“可持久化”技术来优化。
以从序列5 4 2的线段树到序列5 4 2 6的线段树,更新值6的数量操作为例:

不难发现,要将节点6的cnt加1,并不需要完整新建一棵线段树,只会影响从节点[6,6]到根节点一条路径,因此只需要将节点[6,6],[4,6],[1,6]复制出来,将其cnt加1即可,这样每次操作只会新增logn的节点,空间复杂度缩减至O(n * 4 + n*logn)。
要实现上述操作,线段树节点的定义就与之前线段树不太一样了,我们将节点定义为:
struct Node
{
int L, R; //L:左儿子编号 R:右儿子编号
int cnt; //节点所表示的值域区间的元素个数
} tr[N * 24];再用一个int数组来保存每一棵复制出来的新线段树的根节点:
int root[N]; //维护n + 1棵线段树的根节点节点的编号,在创建和复制的时候进行递增来生成
int idx; //线段树节点编号,新增节点时递增++idx例如初始空线段树根节点为root[0],到序列5 4 2时线段树的根节点为root[3],序列5 4 2 6时线段树的根节点为root[4]

4、核心操作
a、build:初始化线段树
建立线段树,cnt初始都是0,将根节点赋值给root[0]。
代码实现如下:
//建立初始线段树,区间范围为l~r
int build(int l, int r)
{
int u = ++idx;
if(l == r) return u;
else
{
int mid = l + r >> 1;
tr[u].L = build(l, mid); //递归建立左子树
tr[u].R = build(mid + 1, r); //递归建立右子树
}
return u;
}b、update:在线段树中将a[i]加1
依次处理序列,对于每个值a[i],要将前一棵线段树root[i-1]的值是a[i]的叶子节点到根节点都进行复制,并将所有节点的cnt加1,生成新的根节点编号赋值给root[i]。
代码实现如下:
//在根节点为pre的权值线段树中将权值x的个数加1,返回新生成的根节点,l、r表示节点所在区间
int update(int pre, int l, int r, int x, int v)
{
int u = ++idx;
//复制pre节点到u,左右子树都复制,cnt加1
tr[u].L = tr[pre].L;
tr[u].R = tr[pre].R;
tr[u].cnt = tr[pre].cnt + 1;
if(l == r) return u; //到叶子节点则返回
int mid = l + r >> 1;
if(x <= mid) tr[u].L = update(tr[u].L, l, mid, x, v); //在左子树递归找x,左子结点应该复制
else tr[u].R = update(tr[u].R, mid + 1, r, x, v); //在右子树递归找x,右子节点应该复制
return u;
}c、find_kth:在[l,r]值域范围查询第k大
先找到root[r]和root[l-1]为根的两棵线段树,[l,r]范围内在左子树的元素个数为:leftcnt = root[r]的左子树的元素个数 - root[l-1]的左子树的元素个数;
再将k与leftcnt比较,如果k <= leftcnt,则应该往root[r]和root[l-1]的左子树去查询;
否则,应该往root[r]和root[l-1]的右子树去查询。
代码实现如下:
//在根节点是left,right的线段树中查询第k小,l、r表示节点所在区间
int find_kth(int l, int r, int left, int right, int k)
{
//计算查询区间范围内所有左子树的元素个数
int leftcnt = tr[tr[right].L].cnt - tr[tr[left].L].cnt;
if(l == r) return l; //到叶子节点,说明找到第k小
int mid = l + r >> 1;
if(k <= leftcnt) return find_kth(l, mid, tr[left].L, tr[right].L, k);
else return find_kth(mid + 1, r, tr[left].R, tr[right].R, k - leftcnt);
}5、离散化
需要注意,值的范围是0≤ai≤10^9,要进行离散化处理。
整体流程请参考代码注释。
100分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 200005;
struct Node
{
int L, R; //L:左儿子编号 R:右儿子编号
int cnt; //节点所表示的值域区间的元素个数
} tr[N * 24];
int root[N]; //维护n + 1棵线段树的根节点
int idx; //线段树节点编号,新增节点时递增++idx
int a[N], n, m; //a是n个整数的序列
vector<int> b; //用于对a排序去重离散化
//获取x离散化之后的值
int lsh(int x)
{
return lower_bound(b.begin(), b.end(), x) - b.begin() + 1;
}
//建立初始线段树,区间范围为l~r
int build(int l, int r)
{
int u = ++idx;
if(l == r) return u;
else
{
int mid = l + r >> 1;
tr[u].L = build(l, mid); //递归建立左子树
tr[u].R = build(mid + 1, r); //递归建立右子树
}
return u;
}
//在根节点为pre的权值线段树中将权值x的个数加1,返回新生成的根节点,l、r表示节点所在区间
int update(int pre, int l, int r, int x, int v)
{
int u = ++idx;
//复制pre节点到u,左右子树都复制,cnt加1
tr[u].L = tr[pre].L;
tr[u].R = tr[pre].R;
tr[u].cnt = tr[pre].cnt + 1;
if(l == r) return u; //到叶子节点则返回
int mid = l + r >> 1;
if(x <= mid) tr[u].L = update(tr[u].L, l, mid, x, v); //在左子树递归找x,左子结点应该复制
else tr[u].R = update(tr[u].R, mid + 1, r, x, v); //在右子树递归找x,右子节点应该复制
return u;
}
//在根节点是left,right的线段树中查询第k小,l、r表示节点所在区间
int find_kth(int l, int r, int left, int right, int k)
{
//计算查询区间范围内所有左子树的元素个数
int leftcnt = tr[tr[right].L].cnt - tr[tr[left].L].cnt;
if(l == r) return l; //到叶子节点,说明找到第k小
int mid = l + r >> 1;
if(k <= leftcnt) return find_kth(l, mid, tr[left].L, tr[right].L, k);
else return find_kth(mid + 1, r, tr[left].R, tr[right].R, k - leftcnt);
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
b.push_back(a[i]);
}
//排序、去重
sort(b.begin(), b.end());
b.erase(unique(b.begin(), b.end()), b.end());
//建立初始线段树,根节点赋值root[0]
root[0] = build(1, b.size());
for(int i = 1; i <= n; i++)
{
//在以root[i-1]为根的线段树中将a[i]离散化后的 个数加1,生成新的线段树根节点赋值给root[i]
root[i] = update(root[i - 1], 1, b.size(), lsh(a[i]), 1);
}
int l, r, k;
while(m--)
{
cin >> l >> r >> k;
int res = find_kth(1, b.size(), root[l - 1], root[r], k);
cout << b[res - 1] << endl; //恢复离散化之前的值
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识?