洛谷题单指南-线段树-P1471 方差

原题链接：https://www.luogu.com.cn/problem/P1471

题意解读：给定序列a[n]，支持三种操作：1.将区间每个数加上一个数 2.查询区间的平均数 3、查询区间的方差

解题思路：要支持区间修改和查询，首选线段树，下面看线段树节点需要维护的信息

平均数 = 区间和 / n，所以第一个要维护的信息是区间和

再将计算方差的公式展开：

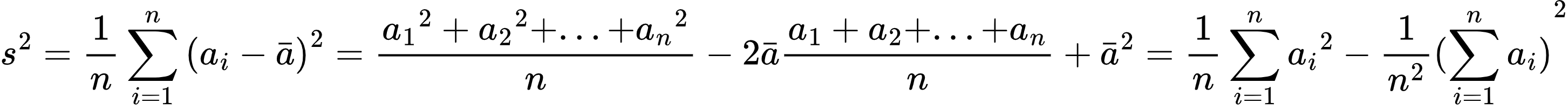
因此，除了维护区间和，还需要维护区间平方和

由于要进行区间修改，需要用到懒标记，定义节点为：

struct  Node
{
    int l, r;
    double sum1; //区间[l,r]的和
    double sum2; //区间[l,r]的平方和
    double add; //懒标记，表示将所有子节点对应区间每一个数增加add
} tr[N * 4];

由区间和以及区间平方和的定义可知，pushup操作为：

void pushup(Node &root, Node &left, Node &right)
{
    root.sum1 = left.sum1 + right.sum1;
    root.sum2 = left.sum2 + right.sum2;
}

void pushup(int u)
{
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

当执行区间修改操作时，如给区间[l,r]每个数增加k

则有sum1 = sum1 + k * (r-l+1)

而每个数增加k，平方和公式可以展开为：

则有sum2 = sum2 + 2 * k * sum1 + (r-l+1) * k * k

注意，sum2依赖的sum1是没有加k之前的，所以要先计算sum2，再计算sum1

所以，添加懒标记以及pushdown操作为：

void addtag(int u, double k)
{
    tr[u].sum2 += 2 * k * tr[u].sum1 + k * k * (tr[u].r - tr[u].l + 1);
    tr[u].sum1 += k * (tr[u].r - tr[u].l + 1);
    tr[u].add += k;
}

void pushdown(int u)
{
    addtag(u << 1, tr[u].add);
    addtag(u << 1 | 1, tr[u].add);
    tr[u].add = 0;
}

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100005;

struct  Node
{
    int l, r;
    double sum1; //区间[l,r]的和
    double sum2; //区间[l,r]的平方和
    double add; //懒标记，表示将所有子节点对应区间每一个数增加add
} tr[N * 4];
double a[N];
int n, m;

void pushup(Node &root, Node &left, Node &right)
{
    root.sum1 = left.sum1 + right.sum1;
    root.sum2 = left.sum2 + right.sum2;
}

void pushup(int u)
{
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r)
{
    tr[u] = {l, r};
    if(l == r) tr[u].sum1 = a[l], tr[u].sum2 = a[l] * a[l];
    else 
    {
        int mid = l + r >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

void addtag(int u, double k)
{
    tr[u].sum2 += 2 * k * tr[u].sum1 + k * k * (tr[u].r - tr[u].l + 1);
    tr[u].sum1 += k * (tr[u].r - tr[u].l + 1);
    tr[u].add += k;
}

void pushdown(int u)
{
    addtag(u << 1, tr[u].add);
    addtag(u << 1 | 1, tr[u].add);
    tr[u].add = 0;
}

Node query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u];
    else if(tr[u].l > r || tr[u].r < l) return Node{};
    else
    {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        Node res = {};
        Node left = query(u << 1, l, r);
        Node right = query(u << 1 | 1, l, r);
        pushup(res, left, right);
        return res;
    }
}

void update(int u, int l, int r, double k)
{
    if(tr[u].l >= l && tr[u].r <= r) addtag(u, k);
    else if(tr[u].l > r || tr[u].r < l) return;
    else 
    {
        pushdown(u);
        update(u << 1, l, r, k);
        update(u << 1 | 1, l, r, k);
        pushup(u);
    }
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    int op, x, y;
    double k; //非常关键，注意如果定义int将得0分
    while(m--)
    {
        cin >> op >> x >> y;
        if(op == 1)
        {
            cin >> k;
            update(1, x, y, k);
        }
        else if(op == 2) cout << fixed << setprecision(4) << query(1, x, y).sum1 / (y - x + 1) << endl;
        else 
        {
            Node res = query(1, x, y);
            n = y - x + 1;
            cout << fixed << setprecision(4) << res.sum2 / n - res.sum1 * res.sum1 / n / n << endl;
        }
    }
    return 0;
}