洛谷题单指南-线段树-P3372 【模板】线段树 1
原题链接：https://www.luogu.com.cn/problem/P3372
题意解读：我们知道，对于一个序列，单点修改区间求和或者区间修改单点求和都可以借助树状数组，而求区间最值可以借助ST表，如果既要进行区间修改，又要进行区间求和或者求最值等其他查询操作，且复杂度都在O(logn)，可以借助线段树。
解题思路：
1、线段树介绍
线段树是一种维护区间信息的树形数据结构，如何将区间用树的节点来表示呢？
设区间[1, n]，n是区间长度，线段树的根节点表示区间[1, n];
一般情况下，设区间是[l, r]，mid = (l + r) / 2，对于一个表示区间[l, r]的节点，
其左子节点表示的区间为[l, mid]，其右子节点表示的区间为[mid + 1, r]；
因此，一个长度为10的区间所表示的线段树各节点如图所示（绿色为叶子节点，表示每个元素）：
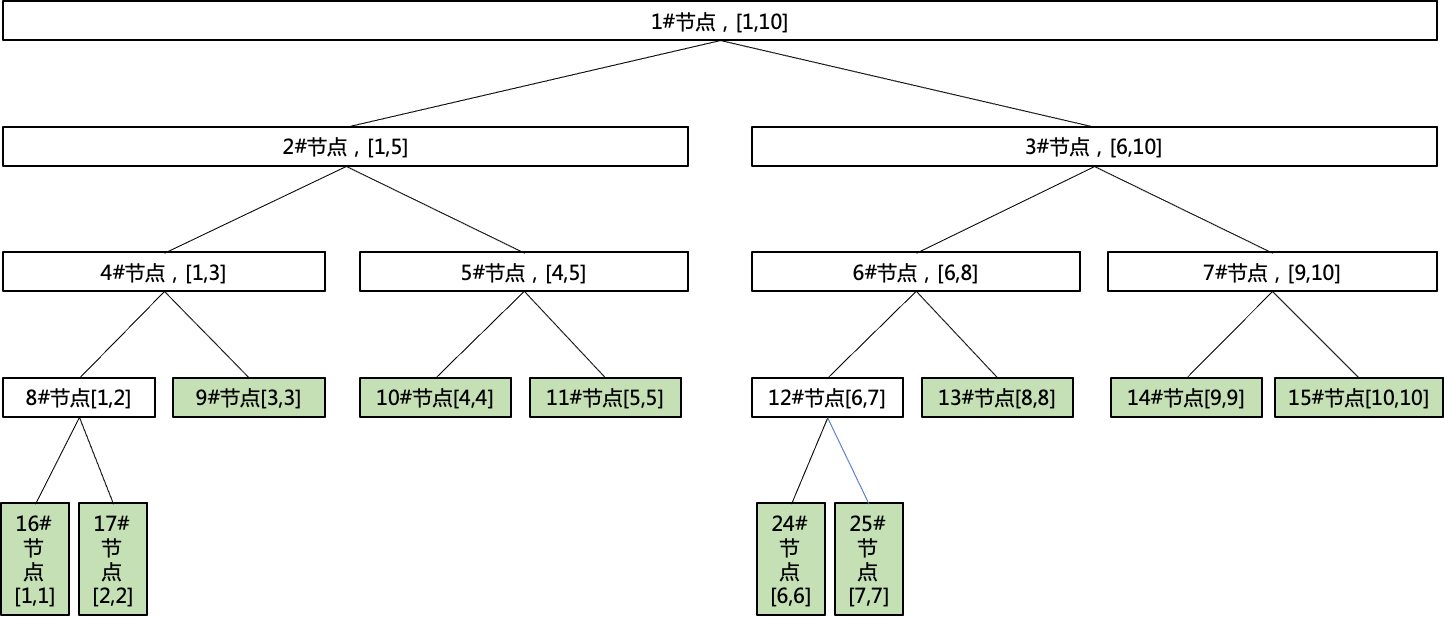
树的存储：如图是采用堆式存储，用数组下标代表节点编号，根节点编号1，对应左子结点2，右子节点3，依次类推。因此对于一个节点u，其左子节点为u * 2，编程时也可以写作u << 1，其右子节点为u * 2 + 1，编程时也可以写作u << 1 | 1。
树的大小：定义数组时，开多大空间合适？我们知道，这颗树除了叶子节点，其余节点都有两个孩子，叶子节点一共有n个，有两个孩子的节点为n-1个，一共2n-1个有效节点，倒数第二层最多也小于n个节点（不可能都是叶子），因此最后一层不会超过2n个节点，加在一起不会超过4n-1个节点，因此空间开N * 4即可。
树的高度：由于是对区间不断进行二分建立树的节点，树的高度为logn。
信息维护：树的节点除了维护区间信息，还可以维护要查询的信息，对于本题就是区间和，可以用结构体来定义树的节点
struct Node
{
int l, r;
int sum;
} tr[N * 4]将若干个子节点的信息合并，就可以得到相应区间的信息，例如，区间[1, 5]的和 = 区间[1, 3]的和 + 区间[4, 5]的和。
因此，线段树能维护的信息必须是可合并的（如区间和，区间最值）。
线段树的节点信息合并可以封装为一个pushup函数：
void pushup(int u)
{
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}2、线段树建立
可以通过递归的方式建立线段树，从根节点开始，依次递归建立左子树、右子树，然后调用pushup将左右信息合并，
如果区间的左、右端点相等，显然是叶子节点，叶子节点的sum值即元素值。
建立线段树的代码为：
//建立线段树
void build(int u, int l, int r)
{
tr[u] = {l, r};
if(l == r) tr[u].sum = a[l];
else
{
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}时间复杂度：每一次递归都会创建一个节点，一共2n-1个节点，创建线段树总体时间复杂度为O(n)
3、单点查询
要查询第x个节点的值，可以从根节点u开始，看x是在u代表区间的左半部分(x <= mid)还是右半部分(x > mid)，
在左半部分则取左子树查找，在右半部分则在右子树查找，直到定位到的节点区间左端点等于右端点且等于x，返回节点的信息即可。
如图所示为查找x=3的节点过程：
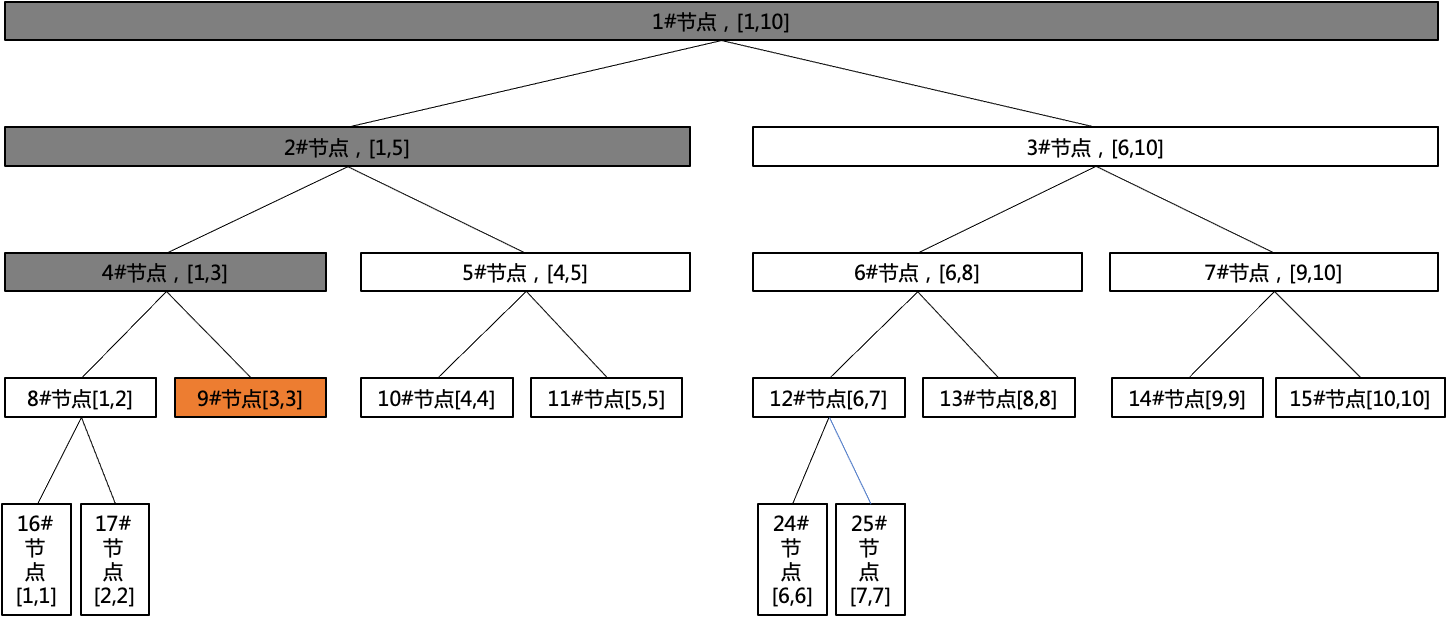
单点查询的代码为：
//查询第x个元素
LL query1(int u, int x)
{
if(tr[u].l == tr[u].r) return tr[u].sum;
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) return query1(u << 1, x);
else return query1(u << 1 | 1, x);
}时间复杂度：O(logn)
4、单点修改
与单点查询类似，首先也是定位到要修改的叶子节点，修改节点的值。
需要注意的是，在递归修改左子树和右子树之后，要调用一次pushup将信息重新合并，更新当前节点的信息。
单点修改的代码为：
//修改第x个元素为k
void update1(int u, int x, LL k)
{
if(tr[u].l == tr[u].r) tr[u].sum = a[x];
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) update1(u << 1, x, k);
else update1(u << 1 | 1, x, k);
pushup(u); //注意要更新u节点的信息
}
}时间复杂度：O(logn)
5、区间查询
线段树的关键是区间操作，如要查询区间[3,7]的元素和，从根节点开始，看当前节点所表示区间与[3,7]的关系
如果当前节点区间完全被[3,7]包含，直接返回当前区间的和；
如果当前节点区间与[3,7]不相交，则返回0，不再继续递归；
如果当前节点区间与[3,7]相交，则递归在当前节点的左子树、右子树去分别查询[3,7]的元素和，再将结构进行加总合并。
如图所示为查询[3,7]区间和的过程：
最终结果由区间[3,3],[4,5],[6,7]的和合并而来。
区间查询的代码为：
//查询区间[l,r]的和
LL query(int u, int l, int r)
{
//如果当前节点完全被[l,r]包含,返回节点值
if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
//如果当前节点与[l,r]不相交，返回0
else if(tr[u].l > r || tr[u].r < l) return 0;
//如果当前节点与[l,r]相交，递归从左右子树查询
else
{
return query(u << 1, l, r) + query(u << 1 | 1, l, r);
}
}
时间复杂度：区间查询每次最多向下查2个节点，而其中一半区间总是在下一次不会继续往下了，一共logn次，因此总体复杂度依然是O(logn)
6、区间修改
对于区间修改操作而言，最终是要落到每一个叶子节点，如果每一次修改，都实时反应到叶子结点，那么需要的时间复杂度为O(n)，显然不可以。
因此，引入延迟标记（又叫懒标记lazy tag）来记录节点区间的一些修改信息，对于本题，可以在结构体增加add表示懒标记：
struct Node
{
int l, r;
LL sum, add;
} tr[N * 4]当递归修改区间[l,r]的值时，如给[l,r]增加k，
如果当前节点区间完全被[l,r]包含，则修改当前节点区间的信息sum += (r-l+1) * k，并给当前节点懒标记赋值add += k，懒标记的值表示当前节点的所有子节点都要加上add；因此，线段树能维护的懒标记必须是可累加的（如加法，异或）。
如果当前节点区间与[l,r]不相交，则不做任何操作；
如果当前节点区间与[l,r]相交，则递归修改左子树、右子树，需要注意的是，在递归修改左右子树之前，可能当前节点有懒标记，需要先将懒标记传给子节点，然后递归修改结束后要调用pushup更新当前节点信息。
同理，在做区间查找操作时，递归查找当前节点的左右子树之前，也需要将当前懒标记传给子节点，确保数据一致性。
如图所示，要将区间[3,7]的每个数增加5，修改操作过程为：
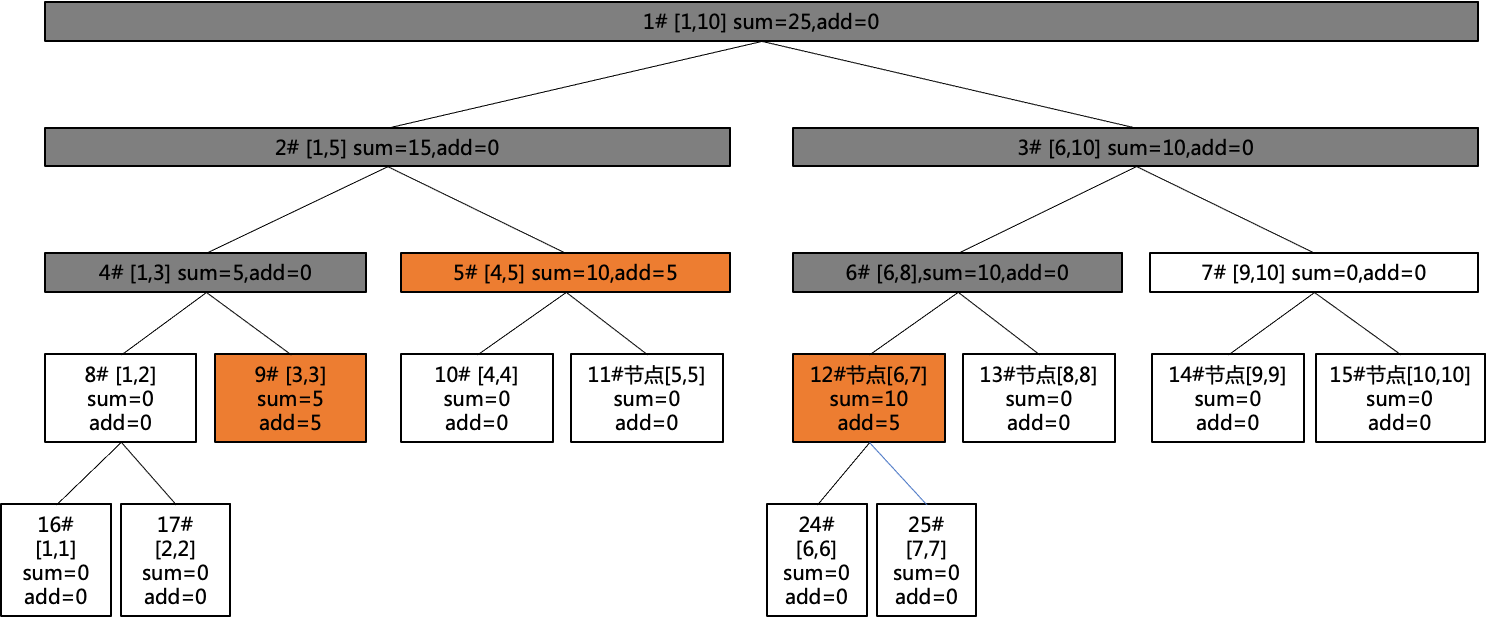
可以看到，修改操作的节点止于[3,3],[4,5],[6,7]，通过更新这三个节点的sum，即可合并出上层整体的sum，且[3,3],[4,5],[6,7]的tag都是5，表示其下的所有子节点都要增加5。
当要查询区间[5,6]的和时，查询过程如下：
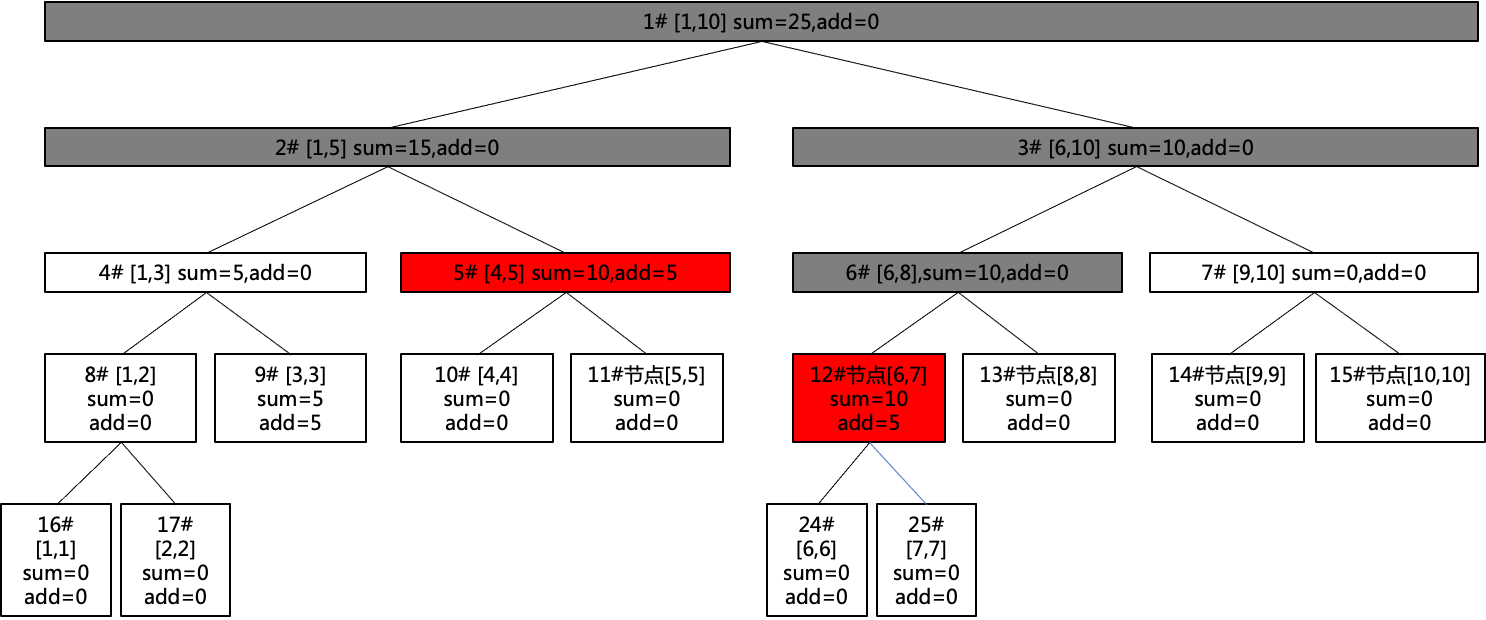
可以看到，查询区间[5,6]的路径一定会经过[4,5]和[6,7]，但此时[4,5]的add=5，[6,7]的add=5，代表其下所有子节点都比较加5，需要在继续递归前将懒标记向下传递，也就是将[4,5]，[6,7]的所有子节点的值加上其父节点的懒标记值，并将子节点的懒标记赋值为父节点的懒标记，然后清空[4,5]，[6,7]的懒标记，如图所示：
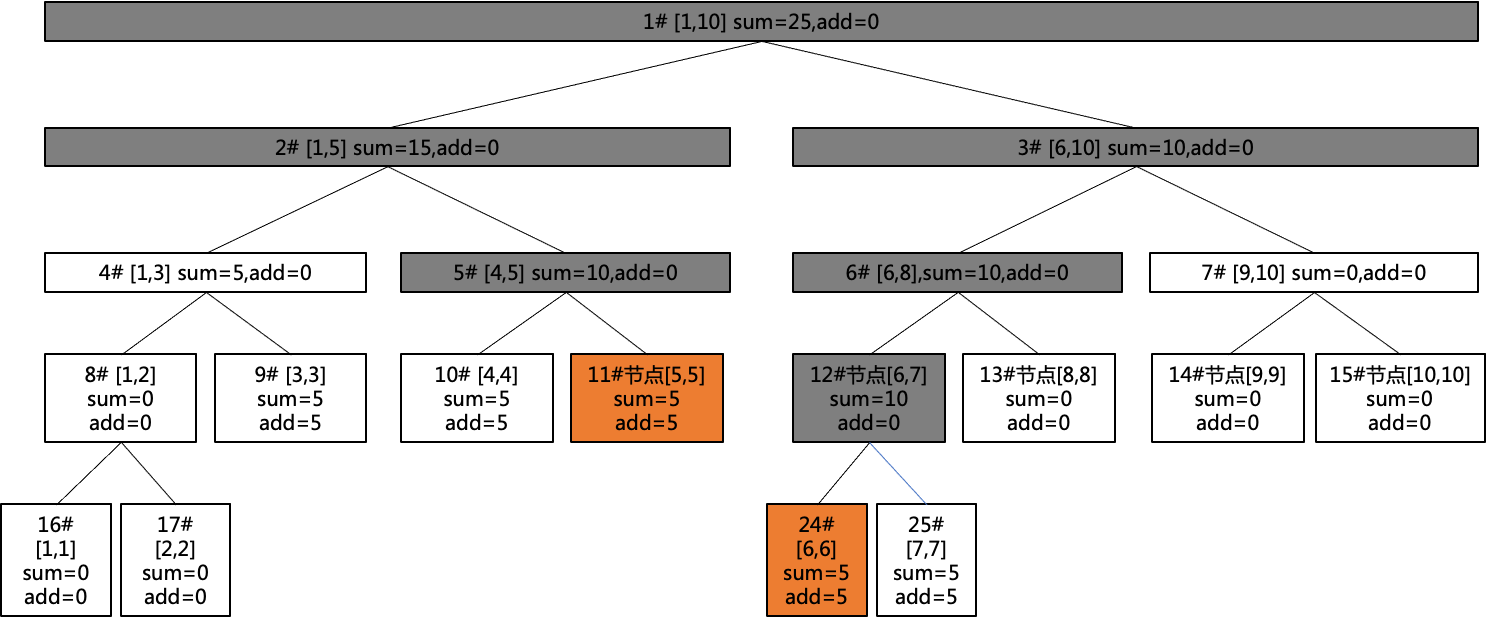
在查询定位到[5,5],[6,6]之前，他们的sum值和add值都已经提前下传过了，因此合并两者的值可以得到正确的结果。
修改当前节点并给懒标记赋值的操作可以封装为函数addtag：
void addtag(int u, LL add)
{
tr[u].sum += (tr[u].r - tr[u].l + 1) * add;
tr[u].add += add;
}将懒标记向下传递的操作可以封装为函数pushdown：
void pushdown(int u)
{
if(tr[u].add)
{
addtag(u << 1, tr[u].add);
addtag(u << 1 | 1, tr[u].add);
tr[u].add = 0;
}
}区间修改的代码为：
//将区间[l,r]每个元素加上k
void update(int u, int l, int r, LL k)
{
//如果当前节点完全被[l,r]包含,添加懒标记
if(tr[u].l >= l && tr[u].r <= r) addtag(u, k);
//如果当前节点与[l,r]不相交，不做任何修改
else if(tr[u].l > r || tr[u].r < l) return;
//如果当前节点与[l,r]相交，递归在左右子树修改
else
{
pushdown(u); //注意在递归前要下传懒标记
update(u << 1, l, r, k);
update(u << 1 | 1, l, r, k);
pushup(u); //注意在修改子节点后要更新u节点值
}
}区间查询代码修改为：
//查询区间[l,r]的和
LL query(int u, int l, int r)
{
//如果当前节点完全被[l,r]包含,返回节点值
if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
//如果当前节点与[l,r]不相交，返回0
else if(tr[u].l > r || tr[u].r < l) return 0;
//如果当前节点与[l,r]相交，递归从左右子树查询
else
{
pushdown(u); //注意在递归前要下传懒标记
return query(u << 1, l, r) + query(u << 1 | 1, l, r);
}
}时间复杂度：由于修改操作不会最终定位所有叶子节点去修改，与区间查询是一样的搜索路径，只在下次要使用节点之前进行懒标记的传递更新，这样能保证数据一致性，因此总体复杂度还是O(logn)
回到题目，只需要实现线段树常见、区间查询、区间修改操作即可，一共有6个核心函数：pushup,pushdown,build,addtag,query,update。
100分代码：
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100005;
struct Node
{
int l, r; //[l,r]是节点表示的区间
LL sum, add; //sum是区间和，add是懒标记表示所有子节点应该增加的值
} tr[N * 4];
LL a[N];
int n, m;
void pushup(int u)
{
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void addtag(int u, LL add)
{
tr[u].sum += (tr[u].r - tr[u].l + 1) * add;
tr[u].add += add;
}
void pushdown(int u)
{
if(tr[u].add)
{
addtag(u << 1, tr[u].add);
addtag(u << 1 | 1, tr[u].add);
tr[u].add = 0;
}
}
//建立线段树
void build(int u, int l, int r)
{
tr[u] = {l, r};
if(l == r) tr[u].sum = a[l];
else
{
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
//查询区间[l,r]的和
LL query(int u, int l, int r)
{
//如果当前节点完全被[l,r]包含,返回节点值
if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
//如果当前节点与[l,r]不相交，返回0
else if(tr[u].l > r || tr[u].r < l) return 0;
//如果当前节点与[l,r]相交，递归从左右子树查询
else
{
pushdown(u); //注意在递归前要下传懒标记
return query(u << 1, l, r) + query(u << 1 | 1, l, r);
}
}
//将区间[l,r]每个元素加上k
void update(int u, int l, int r, LL k)
{
//如果当前节点完全被[l,r]包含,添加懒标记
if(tr[u].l >= l && tr[u].r <= r) addtag(u, k);
//如果当前节点与[l,r]不相交，不做任何修改
else if(tr[u].l > r || tr[u].r < l) return;
//如果当前节点与[l,r]相交，递归在左右子树修改
else
{
pushdown(u); //注意在递归前要下传懒标记
update(u << 1, l, r, k);
update(u << 1 | 1, l, r, k);
pushup(u); //注意在修改子节点后要更新u节点值
}
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> a[i];
build(1, 1, n);
int op, x, y;
LL k;
while(m--)
{
cin >> op;
if(op == 1)
{
cin >> x >> y >> k;
update(1, x, y, k);
}
else
{
cin >> x >> y;
cout << query(1, x, y) << endl;
}
}
}
