洛谷题单指南-二叉堆与树状数组-P2168 [NOI2015] 荷马史诗

原题链接：https://www.luogu.com.cn/problem/P2168

题意解读：把单次替换成k进制字符串，使得替换后文本内容最短，典型的哈夫曼编码应用。

解题思路：

要把单词转成k进制字符串，根据哈夫曼编码的原理，可以依次将k个出现次数最少的单词进行合并，最后得到一棵树，每个非叶节点应该有k个子节点，

每个子节点路径权值对应0,1....k-1，然后对所有单词按照路径权值进行编码即可。

比如样例2：

6 3
1
1
3
3
9
9

生成的哈夫曼树为：

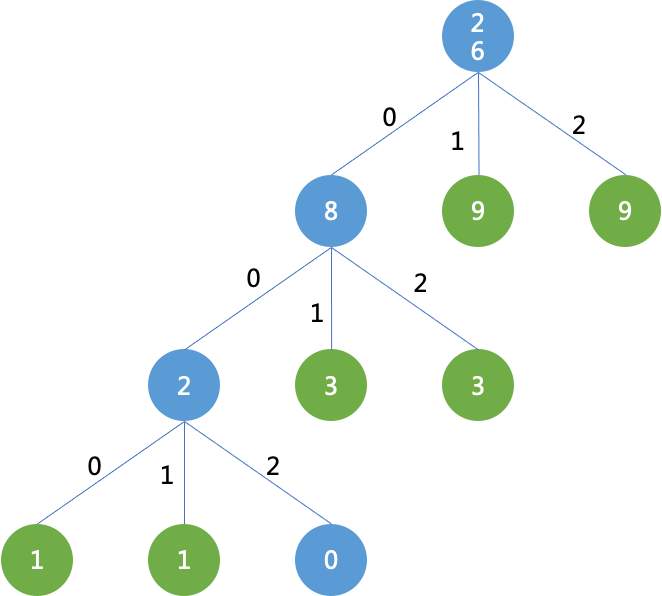
最终编码如下：

出现次数为1的单词：000

出现次数为1的单词：001

出现次数为3的单词：01

出现次数为3的单词：02

出现次数为9的单词：1

出现次数为9的单词：2

因此，编码后总长度为1*3+1*3+3*2+9*1+9*1 = 36，最长的编码长度是3。

需要注意，每次需要合并3个单词节点，由于总数量为6，需要补一个次数为0的单词节点，

如果是k进制，共n个单词，补充节点数量为 k-1 - (n - 1）% (k - 1) ，原因为：每次合并都会减少k - 1个节点，最后剩1个节点, 一共减少了n - 1个节点，当然，如果(n - 1）% (k - 1) == 0，不需要补充节点。

对于要选择k个最小的数，可以借助于优先队列。

对于编码，实际不需要求出每个单词的编码，只需要在合并过程中记录每个节点的最大高度，根据根节点的高度可得到编码长度。

每次合并的结果，都追加到答案，最终答案就是编码后的文章总长度。

100分代码：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
int n, k;
struct Node
{
    ll cnt; //单词出现次数
    ll depth; //节点所在高度,从叶子往上增加
    bool operator < (const Node &x) const
    {
        if(cnt != x.cnt) return cnt > x.cnt; //小根堆
        return depth > x.depth; //高度小的优先
    }
};
priority_queue<Node> q;
ll ans;

int main()
{
    cin >> n >> k;
    ll x;
    for(int i = 1; i <= n; i++)
    {
        cin >> x;
        q.push({x, 0});
    } 
    //补0
    if((n - 1) % (k - 1) != 0)
    {
        for(int i = 1; i <= k - 1 - (n - 1) % (k - 1); i++)
        {
            q.push({0, 0});
        }
    }
    
    while(q.size() > 1)
    {
        ll sum = 0;
        ll lastdepth = 0;
        for(int i = 1; i <= k; i++)
        {
            sum += q.top().cnt;
            lastdepth = max(lastdepth, q.top().depth); //待合并的k个节点的最大高度
            q.pop();
        }
        q.push({sum, lastdepth + 1}); //合并后节点的高度是待合并节点最大高度+1
        ans += sum; //每次合并，都对答案贡献合并结果
    }
    cout << ans << endl;
    cout << q.top().depth << endl; //最大编码长度是最大高度
}