洛谷题单指南-字符串-P3369 【模板】普通平衡树

原题链接：https://www.luogu.com.cn/problem/P3369

题意解读：平衡树的基本操作，模版题。

解题思路：

1、二叉搜索树-BST

二叉搜索树满足这样的性质：每一个节点的权值大于它的左儿子，小于它的右儿子。

对BST进行中序遍历，将得到一个从小到大的有序序列，因此BST是为了维护一个有序序列的动态添加、删除、查找。

随机情况下，对树进行插入、查找、删除等操作的时间复杂度都是O(logN)，

但是如果插入顺序是一个已经有序的序列，将退化成一条链，时间复杂度变成O(N)。

2、平衡树

平衡树就是为了解决BST中高度不均衡导致时间复杂度上升的问题，

为了使某个节点左右子树高度尽可能差距小，需要进行两个重要的操作：左旋、右旋

左旋：将以E为根的子树左旋，先令S = E->right，再E->right = S->left，然后S->left = E

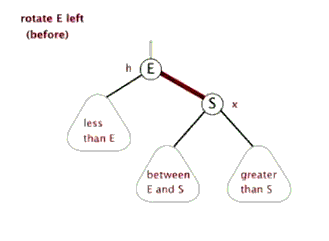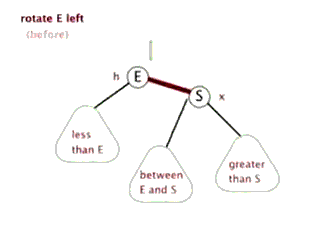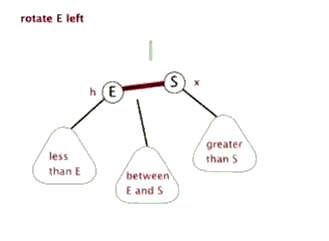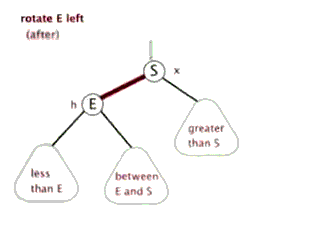
右旋：将以S为根的子树右旋，先令E = S->left，再S->left = E->right，然后E->right = S

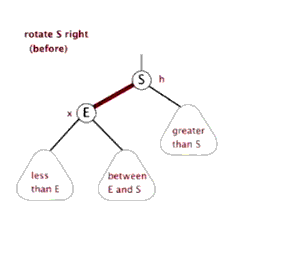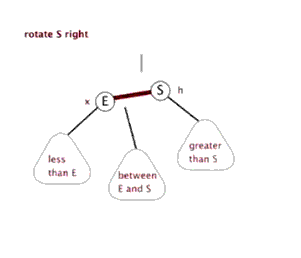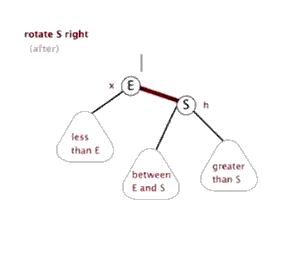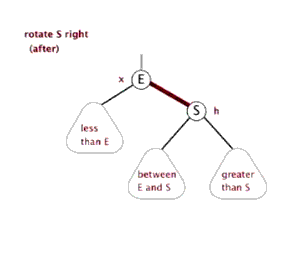
平衡树的具体实现方式有多种，如AVL、红黑树、Treap、Splay、Trie等等，本文主要介绍最好写的两种：Trie、Treap。

3、用01-Trie平替平衡树

为什么01-Trie可以平替平衡树？

首先，01-Trie高度是固定的，显然满足平衡的特点。

其次，01-Trie也满足左子树对应的值更小，右子树对应的值更大，能够维护序列的有序性。

最后，01-Trie实现平衡树，需要记录一些额外的信息：每个结点所在子树一共有有多个元素

但是，01-Trie作为平衡树也有一些缺点，比如：

占用空间较大，每个整数都拆成二进制作为树的节点。

不能处理负数，但是可以加上一个较大的数将负数转正。

在数据量不太大的情况下，还是可以使用的。

Trie实现平衡树的基本操作：

本题元素大小|x|<=10^7

设int trie[N * 26][2], idx表示Trie树，int siz[N * 26]记录每个节点所在子树的元素个数。

a、插入

void add(int val)
{
    int u = 0;
    for(int i = 25; i >= 0; i--)
    {
        int v = val >> i & 1;
        if(!trie[u][v]) trie[u][v] = ++idx;
        u = trie[u][v];
        siz[u]++;
    }
}

b、删除

void del(int val)
{
    int u = 0;
    for(int i = 25; i >= 0; i--)
    {
        int v = val >> i & 1;
        if(!trie[u][v]) return;
        u = trie[u][v];
        siz[u]--;
    }
}

c、查找小于x的元素个数

int get_less(int val)
{
    int res = 0;
    int u = 0;
    for(int i = 25; i >= 0; i--)
    {
        int v = val >> i & 1;
        if(v == 1) res += siz[trie[u][0]]; //如果val在右子树，则左子树所有数都是小于val的，要累加
        u = trie[u][v];
        if(!u) break; //如果val不存在，到这里就可以结束
    }
    return res;
}

d、查找第k个数

int get_kth(int k)
{
    int res = 0;
    int u = 0;
    for(int i = 25; i >= 0; i--)
    {
        if(siz[trie[u][0]] < k) //左子树数量不足k，在右子树找
        {
            k -= siz[trie[u][0]]; //k要减去左子树的数量
            u = trie[u][1];
            res = res * 2 + 1;
        } 
        else 
        {
            u = trie[u][0];
            res = res * 2;
        }
        if(!u) break;
    }
    return res - INF;
}

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100005, INF = 1e7;

int trie[N * 26][2], idx;
int siz[N * 26]; //siz[i]表示节点i所在子树中数的个数，根节点不需要记录

//插入元素到trie
void add(int val)
{
    int u = 0;
    for(int i = 25; i >= 0; i--)
    {
        int v = val >> i & 1;
        if(!trie[u][v]) trie[u][v] = ++idx;
        u = trie[u][v];
        siz[u]++;
    }
}

//从trie中删除元素
void del(int val)
{
    int u = 0;
    for(int i = 25; i >= 0; i--)
    {
        int v = val >> i & 1;
        if(!trie[u][v]) return;
        u = trie[u][v];
        siz[u]--;
    }
}

//获取小于val的元素数量
int get_less(int val)
{
    int res = 0;
    int u = 0;
    for(int i = 25; i >= 0; i--)
    {
        int v = val >> i & 1;
        if(v == 1) res += siz[trie[u][0]];
        u = trie[u][v];
        if(!u) break; //如果val不存在，到这里就可以结束
    }
    return res;
}

//获取排名第k的元素
int get_kth(int k)
{
    int res = 0;
    int u = 0;
    for(int i = 25; i >= 0; i--)
    {
        if(siz[trie[u][0]] < k) //左子树数量不足k，在右子树找
        {
            k -= siz[trie[u][0]];
            u = trie[u][1];
            res = res * 2 + 1;
        } 
        else 
        {
            u = trie[u][0];
            res = res * 2;
        }
        if(!u) break;
    }
    return res - INF;
}

int main()
{
    int n;
    cin >> n;
    int opt, x;
    while(n--)
    {
        cin >> opt >> x;
        if(opt == 1) x += INF, add(x); //元素值+INF，使得必然为非负数，才能加入01trie
        else if(opt == 2) x += INF, del(x);
        else if(opt == 3) x += INF, cout << get_less(x) + 1 << endl;
        else if(opt == 4) cout << get_kth(x) << endl;
        else if(opt == 5) x += INF, cout << get_kth(get_less(x)) << endl;
        else x += INF, cout << get_kth(get_less(x + 1) + 1) << endl;
    }
    return 0;
}

4、Treap平衡树

Treap是Tree+Heap，也就是树+堆，通过树来维护BST结构，通过堆的性质来保证尽可能平衡。

具体来说，树的节点定义为：

struct Node
{
    int l, r; //l左子树，r右子树
    int val, pri; //val是节点权值，pri是随机数用来维护堆的性质
    int siz, cnt; //siz是节点为根的子树大小，cnt是节点重复元素的个数
} tr[N];
int idx; //树节点编号
int root; //根节点

通过val来维护BST的性质，如果val严格有序将导致树退化成链，因此引入一个随机数pri，并强制父节点的pri大于子节点pri（大根堆性质），通过维护此性质即可保持树的平衡。

通过siz，cnt这些附加信息，就可以实现查元素排名、查第k个元素、找前驱、找后继等操作。

Treap维护树的平衡只需要在插入元素的时候判断，如果插入元素后，导致子节点的pri大于父节点的pri，则进行相应的旋转操作（左旋or右旋）。

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100005, INF = 1e8;

struct Node
{
    int l, r; //l左子树，r右子树
    int val, pri; //val是节点权值，pri是随机数用来维护堆的性质
    int siz, cnt; //siz是节点为根的子树大小，cnt是节点重复元素的个数
} tr[N];
int idx; //树节点编号
int root; //根节点

//生成一个新节点
int get_node(int val)
{
    tr[++idx].val = val;
    tr[idx].pri = rand(); //随机值，通过维护大根堆特性确保尽量平衡
    tr[idx].siz = tr[idx].cnt = 1;
    return idx;
}

//计算子树siz
void pushup(int &p)
{
    tr[p].siz = tr[tr[p].l].siz + tr[tr[p].r].siz + tr[p].cnt;
}

//右旋
void rotate_to_r(int &p)
{
    int t = tr[p].l; 
    tr[p].l = tr[t].r;
    tr[t].r = p;
    p = t;
    pushup(tr[p].r);
    pushup(p);
}

//左旋
void rotate_to_l(int &p)
{
    int t = tr[p].r;
    tr[p].r = tr[t].l;
    tr[t].l = p;
    p = t;
    pushup(tr[p].l);
    pushup(p);
}   

//初始化树
void build_tree()
{   
    //树中添加两个初始节点：极大值和极小值，避免出现边界问题
    get_node(-INF); 
    get_node(INF);
    root = 1;
    tr[root].r = 2;
    pushup(root);
    if(tr[1].pri < tr[2].pri) rotate_to_l(root);
}

void insert(int &p, int val)
{
    if(!p) p = get_node(val);
    else if(tr[p].val == val) tr[p].cnt++;
    else if(tr[p].val > val) 
    {
        insert(tr[p].l, val);
        if(tr[tr[p].l].pri > tr[p].pri) rotate_to_r(p); //插入左子树后对不满足堆性质进行调整
    }
    else
    {
        insert(tr[p].r, val);
        if(tr[tr[p].r].pri > tr[p].pri) rotate_to_l(p); //插入右子树后对不满足堆性质进行调整
    }
    pushup(p);
}

void erase(int &p, int val)
{
    if(!p) return;
    else if(tr[p].val == val)
    {
        if(tr[p].cnt > 1) tr[p].cnt--; //找到有多个，减一个
        else if(!tr[p].l && !tr[p].r) //叶子节点，直接删除
        {
            p = 0;
        }
        else if(!tr[p].r || tr[tr[p].l].pri > tr[tr[p].r].pri) 
        { //如果只有左子树，或者左子树pri大于右子树，则右旋，然后去右子树删除
            rotate_to_r(p);
            erase(tr[p].r, val);
        }
        else if(!tr[p].l || tr[tr[p].r].pri > tr[tr[p].l].pri)
        { //如果只有右子树，或者右子树pri大于左子树，则左旋，然后去左子树删除
            rotate_to_l(p);
            erase(tr[p].l, val);
        }
    }
    else if(tr[p].val > val) erase(tr[p].l, val);
    else erase(tr[p].r, val);
    pushup(p);
}

//查询比val小的数的个数，由于第一个节点是-INF，因此比val小的数的个数就是排名
int get_less(int p, int val)
{
    if(!p) return 0; 
    else if(tr[p].val == val) return tr[tr[p].l].siz; //p就是val，则p左子树大小就是比val小的数的个数
    else if(tr[p].val > val) return get_less(tr[p].l, val); //到左子树找
    else if(tr[p].val < val) return tr[p].cnt + tr[tr[p].l].siz + get_less(tr[p].r, val); //到右子树找，p和p的左子树都比val小，要累加
}

//查询第k个数
int get_kth(int p, int k)
{
    if(!p) return 0; //没有找到
    else if(tr[tr[p].l].siz >= k) return get_kth(tr[p].l, k); //到左子树找
    else if(tr[tr[p].l].siz + tr[p].cnt >= k) return tr[p].val; //p就是第k个
    else if(tr[tr[p].l].siz < k) return get_kth(tr[p].r, k - tr[tr[p].l].siz - tr[p].cnt); //到右子树找
}

//查找val的前驱，比val小的最大数
int get_prev(int p, int val)
{
    if(!p) return -INF;
    else if(tr[p].val >= val) return get_prev(tr[p].l, val);
    else return max(tr[p].val, get_prev(tr[p].r, val));
}

//查找val的后继，比val大的最小数
int get_next(int p, int val)
{
    if(!p) return INF;
    else if(tr[p].val <= val) return get_next(tr[p].r, val);
    else return min(tr[p].val, get_next(tr[p].l, val));
}

int main()
{
    int n;
    cin >> n;
    int opt, x;
    build_tree();
    while(n--)
    {
        cin >> opt >> x;
        if(opt == 1) insert(root, x);
        else if(opt == 2) erase(root, x);
        else if(opt == 3) cout << get_less(root, x) << endl;
        else if(opt == 4) cout << get_kth(root, x + 1) << endl;
        else if(opt == 5) cout << get_prev(root, x) << endl;
        else if(opt == 6) cout << get_next(root, x) << endl;
    }
    return 0;
}