洛谷题单指南-字符串-Test
原题链接:https://www.luogu.com.cn/problem/CF25E https://codeforces.com/contest/25/problem/E
题意解读:给定a,b,c三个字符串,求包含a、b、c的最短字符串长度。
解题思路:
要得到包含a、b、c的字符串,可以通过a、b、c连接形成,而要使得连接后的字符串最短,可以尽可能的利用重叠部分
如a、b字符串连接的情况可能有三种:连续、交叉、包含
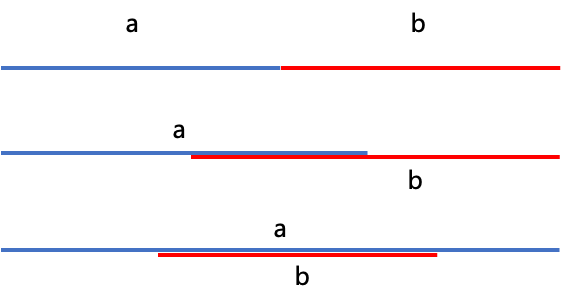
因此,对于a、b字符串连接的最短长度,可以先计算a是否包含b,如果包含b,连接后的长度即a的长度;再计算a后缀与b前缀公共长度ab,连接后长度为a.size()+b.size()-ab。
而a、b、c连接的方式一共有六种:
a->b->c
a->c->b
b->a->c
b->c->a
c->a->b
c->b->a
枚举所有情况下连接后得到的字符串长度,取最短即可。
这里有一个关键函数:int longest(string &x, string &y)
用来计算x后缀与y前缀的最长公共长度,且如果x包含y函数返回-1
STL String暴力枚举:
int longest(string &x, string &y)
{
if(x.find(y) != string::npos) return -1; //如果x包含y
int len = min(x.size(), y.size());
int res = 0;
for(int i = 1; i <= len; i++) //枚举前后缀的公共长度
{
string post = x.substr(x.size() - i, i); //x的后缀
string pre = y.substr(0, i); //y的前缀
if(post == pre) res = i; //判断是否相等
}
return res;
}以上方法是O(n^2)的,必须优化
KMP优化实现:
int longest_kmp(string &x, string &y)
{
memset(Next, 0, sizeof(Next));
//利用y计算Next数组
for(int i = 1, j = 0; i < y.size(); i++)
{
while(j && y[i] != y[j]) j = Next[j - 1];
if(y[i] == y[j]) j++;
Next[i] = j;
}
int j = 0;
//在x中找y,如果找到返回-1,如果没找到,返回y最后匹配的位置即最大公共前后缀长度
for(int i = 0; i < x.size(); i++)
{
while(j && x[i] != y[j]) j = Next[j - 1];
if(x[i] == y[j]) j++;
if(j == y.size()) return -1;
}
return j;
}100分代码:
#include <bits/stdc++.h>
using namespace std;
string a, b, c;
int Next[100005];
//计算相同的x的后缀和y的前缀长度,x包含y时返回-1
int longest(string &x, string &y)
{
if(x.find(y) != string::npos) return -1; //如果x包含y
int len = min(x.size(), y.size());
int res = 0;
for(int i = 1; i <= len; i++) //枚举前后缀的公共长度
{
string post = x.substr(x.size() - i, i); //x的后缀
string pre = y.substr(0, i); //y的前缀
if(post == pre) res = i; //判断是否相等
}
return res;
}
//用KMP优化上面的longest函数
int longest_kmp(string &x, string &y)
{
memset(Next, 0, sizeof(Next));
//利用y计算Next数组
for(int i = 1, j = 0; i < y.size(); i++)
{
while(j && y[i] != y[j]) j = Next[j - 1];
if(y[i] == y[j]) j++;
Next[i] = j;
}
int j = 0;
//在x中找y,如果找到返回-1,如果没找到,返回y最后匹配的位置即最大公共前后缀长度
for(int i = 0; i < x.size(); i++)
{
while(j && x[i] != y[j]) j = Next[j - 1];
if(x[i] == y[j]) j++;
if(j == y.size()) return -1;
}
return j;
}
//计算x->y->z连接顺序下的最短字符串长度
long long calcu(string &x, string &y, string &z, int xy, int yz, int xz)
{
long long res = x.size(); //加上x的长度
if(xy >= 0) //如果y不是x的子串
{
res += y.size() - xy; //加上y的长度,减去y前缀和x后缀重叠部分的长度
if(yz >= 0) res += z.size() - yz; //如果z不是y的子串,加上z的长度,减去z前缀和y后缀重叠部分的长度
}
else //如果y是x的子串
{
if(xz >= 0) res += z.size() - xz; //如果z不是x的子串,加上z的长度,减去z前缀和x后缀重叠部分的长度
}
return res;
}
int main()
{
cin >> a >> b >> c;
int ab = longest_kmp(a, b);
int ba = longest_kmp(b, a);
int bc = longest_kmp(b, c);
int cb = longest_kmp(c, b);
int ca = longest_kmp(c, a);
int ac = longest_kmp(a, c);
long long ans = 1e18, t;
//abc
t = calcu(a, b, c, ab, bc, ac);
ans = min(ans, t);
//acb
t = calcu(a, c, b, ac, cb, ab);
ans = min(ans, t);
//bac
t = calcu(b, a, c, ba, ac, bc);
ans = min(ans, t);
//bca
t = calcu(b, c, a, bc, ca, ba);
ans = min(ans, t);
//cab
t = calcu(c, a, b ,ca, ab, cb);
ans = min(ans, t);
//cba
t = calcu(c, b, a, cb, ba, ca);
ans = min(ans, t);
cout << ans;
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识?