洛谷题单指南-分治与倍增-P6648 [CCC2019] Triangle: The Data Structure

原题链接：https://www.luogu.com.cn/problem/P6648

题意解读：在一个n行的数字三角形中，求所有边长为k的正三角形最大值之和。

解题思路：

1、枚举法

枚举每一个边长为k的三角形，在其中求max，然后累加，n最多3000，时间复杂度是n^4，显然超时。

2、倍增和ST思想

此题非常类似于RMQ问题，也就是求区间最值，只不过区间是一个三角形

可否借助ST思想？

不妨设st[i][j][k]表示从(i,j)开始，大小为2^k的三角形内最大值，a[i][j]表示三角形(i,j)位置的值

初始化：st[i][j][0] = a[i][j]

递推：

求值：

假设要计算(i,j)为顶点，边长为k的三角形内最大值

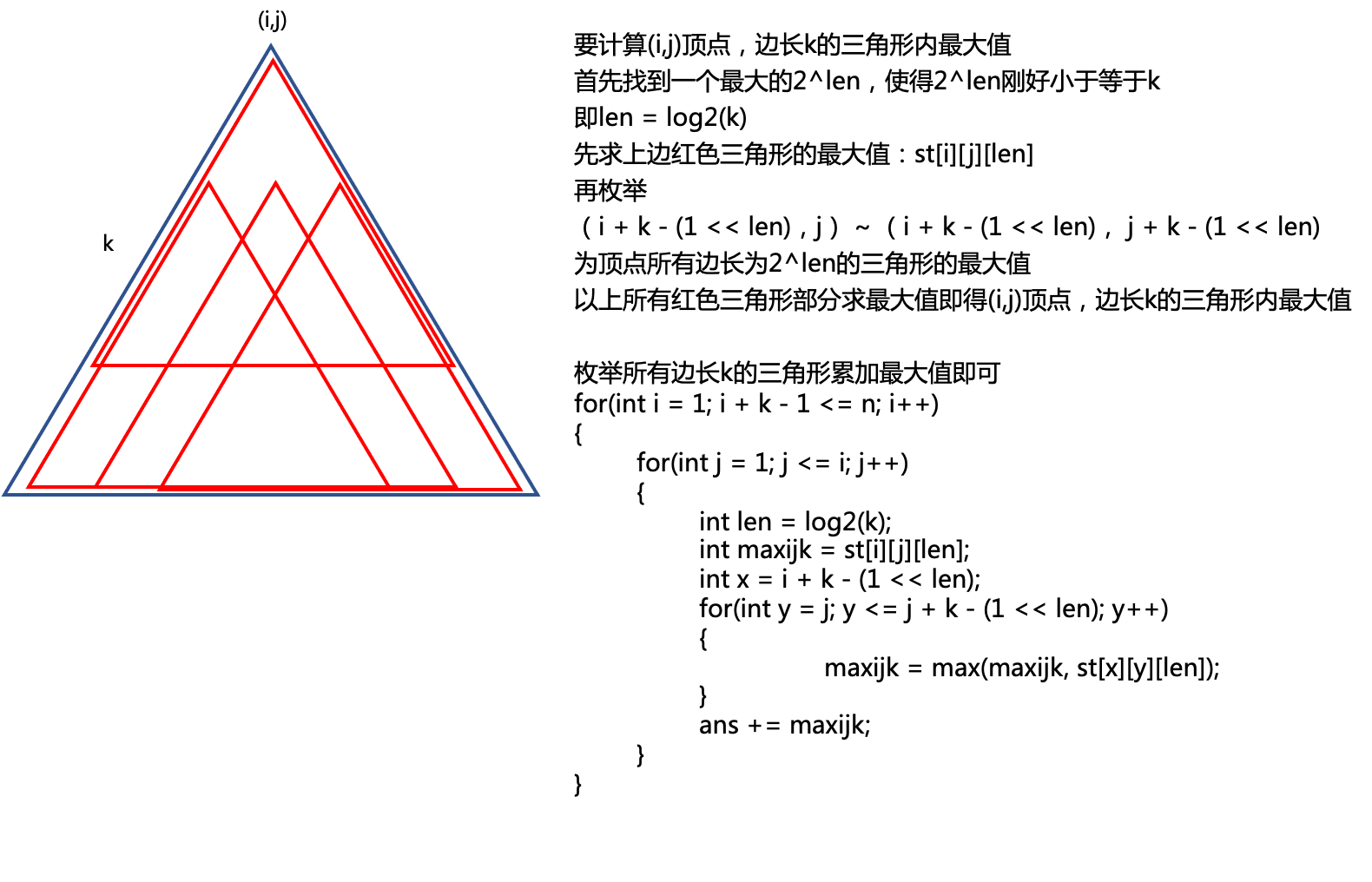
想到这里，兴匆匆的写出如下代码：

0分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 3005;
int a[N][N];
int st[N][N][12]; //st[i][j][k]表示从(i,j)开始，大小为2^k的三角形内最大值
int n, k;
long long ans;

int main()
{
    cin >> n >> k;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= i; j++)
        {
            cin >> a[i][j];
            st[i][j][0] = a[i][j];
        }
    }

    for(int l = 1; l < log2(n); l++)
    {
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= n; j++)
            {
                st[i][j][l] = st[i][j][l - 1];
                int x = i + (1 << l - 1);
                for(int y = j; y <= j + (1 << l - 1); y++)
                {
                    st[i][j][l] = max(st[i][j][l], st[x][y][l - 1]);
                }
            }
        }
    }

    for(int i = 1; i + k - 1 <= n; i++)
    {
        for(int j = 1; j <= i; j++)
        {
            int len = log2(k);
            int maxijk = st[i][j][len];
            int x = i + k - (1 << len);
            for(int y = j; y <= j + k - (1 << len); y++)
            {
                maxijk = max(maxijk, st[x][y][len]);
            }
            ans += maxijk;
        }
    }
    cout << ans;

    return 0;
}

原来是int st[N][N][12]爆内存了，需要进一步优化，递推式中l只依赖l-1，因此可以用滚动数组进行优化，于是有：

25分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 3005;
int a[N][N];
int st[N][N][2]; //st[i][j][k]表示从(i,j)开始，大小为2^k的三角形内最大值，第三维用滚动数组优化
int n, k;
long long ans;

int main()
{
    cin >> n >> k;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= i; j++)
        {
            cin >> a[i][j];
            st[i][j][0] = a[i][j];
        }
    }

    for(int l = 1; l <= log2(k); l++)
    {
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= n; j++)
            {
                st[i][j][l % 2] = st[i][j][(l - 1) % 2];
                int x = i + (1 << l - 1);
                for(int y = j; y <= j + (1 << l - 1); y++)
                {
                    st[i][j][l % 2] = max(st[i][j][l % 2], st[x][y][(l - 1) % 2]);
                }
            }
        }
    }

    for(int i = 1; i + k - 1 <= n; i++)
    {
        for(int j = 1; j <= i; j++)
        {
            int len = log2(k);
            int maxijk = st[i][j][len % 2];
            int x = i + k - (1 << len);
            for(int y = j; y <= j + k - (1 << len); y++)
            {
                maxijk = max(maxijk, st[x][y][len % 2]);
            }
            ans += maxijk;
        }
    }
    cout << ans;

    return 0;
}

究其原因，关键代码的时间复杂度是logk*N^3，需要进一步优化时间

观察代码：

红色框中是要计算从j开始，窗口长度（1<<l-1）+ 1的最大值，显然可以用单调队列优化，于是就有了以下最终版代码：

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 3005;
int a[N][N];
int st[N][N][2]; //st[i][j][k]表示从(i,j)开始，大小为2^k的三角形内最大值，第三维用滚动数组优化
int n, k;
long long ans;
int q[N], head, tail;

int main()
{
    cin >> n >> k;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= i; j++)
        {
            cin >> a[i][j];
            st[i][j][0] = a[i][j];
        }
    }

    for(int l = 1; l <= log2(k); l++)
    {
        for(int i = 1; i <= n; i++)
        {
            head = 1, tail = 0; //单调队列头、尾指针初始化
            int len = (1 << l - 1) + 1; //窗口大小
            int x = i + (1 << l - 1); //起始横坐标
            for(int j = 1; j <= n; j++)
            {
                st[i][j][l % 2] = st[i][j][(l - 1) % 2];
                //去头
                while(head <= tail && j - q[head] + 1 > len) head++;
                //去尾
                while(head <= tail && st[x][j][(l - 1) % 2] > st[x][q[tail]][(l - 1) % 2]) tail--;
                //存入
                q[++tail] = j;   
                //取窗口最大值，并与i，j - len + 1位置对应的值取max
                if(j >= len)
                    st[i][j - len + 1][l % 2] = max(st[i][j - len + 1][l % 2], st[x][q[head]][(l - 1) % 2]);
            }
        }
    }

    for(int i = 1; i + k - 1 <= n; i++)
    {
        for(int j = 1; j <= i; j++)
        {
            int len = log2(k);
            int maxijk = st[i][j][len % 2];
            int x = i + k - (1 << len);
            for(int y = j; y <= j + k - (1 << len); y++)
            {
                maxijk = max(maxijk, st[x][y][len % 2]);
            }
            ans += maxijk;
        }
    }
    cout << ans;

    return 0;
}