洛谷题单指南-分治与倍增-P1966 [NOIP2013 提高组] 火柴排队

原题链接：https://www.luogu.com.cn/problem/P1966

题意解读：计算两个序列∑(ai​−bi​)^2的最小值，对10^8-3取模。

解题思路：

1、贪心思路

要使得两个序列对应位置元素之差的平方和最小，必须满足两个序列相对排序是一致的，什么意思？

设a序列有两个元素：a1，a2，b序列有两个元素b1，b2

当a1<a2，b1<b2时，(a1-b1)^2 + (a2-b2)^2是最小的！

为什么？

可以分析，如果a1<a2 b1>b2，

令：A = (a1-b1)^2 + (a2-b2)^2，B = (a1-b2)^2 + (a2-b1)^2

将A，B展开，相减

B - A = 2a1b1+2a2b2-2a1b2-2a2b1 = 2a1(b1-b2)-2a2(b1-b2)=2(a1-a2)(b1-b2) < 0

所以B更小，也就是b1,b2交换位置之后，再与a1,a2计算距离会更小

所以得出结论：两个序列的相对顺序保持一致是，对应元素之差的平方和最小。

2、逆序对求解

有了以上结论，就可以固定一个序列为标准顺序，然后求将另外一个序列转换成标准顺序需要交换的次数

标准顺序要定义为升序1~n的，另外一个序列转成1~n需要的交换次数就是其逆序对个数。

下面模拟样例：

序列1：1 3 4 2

序列2：1 7 2 4

如果以序列1为基准，先要将序列1的元素进行离散化，这里正好是1~4四个数字，离散化之后也保持不变，我们对每一个元素给定一个序号，已序号的位置为标准顺序

值	1	3	4	2
序号	1	2	3	4

再对序列2进行离散化处理

原值	1	7	2	4
离散化后值	1	4	2	3
序号	1	2	3	4
离散化后值在序列1中的序号	1	3	4	2

接下来，我们的目标是要将

转换为

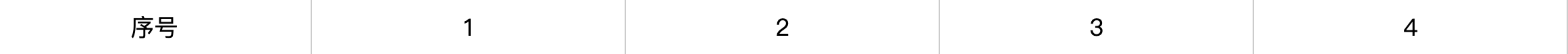
只需要计算1 3 4 2的逆序对数，即为2。

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100005, MOD = 1e8 - 3;

struct node 
{
    int value, idx;
};
int n;
long long ans;
node a[N], b[N];
int h[N], c[N];

bool cmp_value(node x, node y)
{
    return x.value < y.value;
}

bool cmp_idx(node x, node y)
{
    return x.idx < y.idx;
}

void merge(int s1, int e1, int s2, int e2)
{
    int i = s1, j = s2;
    int tmp[e2 - s1 + 1], cnt = 0;
    while(i <= e1 && j <= e2)
    {
        if(c[i] <= c[j]) tmp[++cnt] = c[i++];
        // 如果c[i] > c[j]，则c[i]~c[e1]都会比c[j]大，对逆序对的贡献增加了e1 - i + 1个
        else tmp[++cnt] = c[j++], ans += e1 - i + 1; 
    } 
    while(i <= e1) tmp[++cnt] = c[i++];
    while(j <= e2) tmp[++cnt] = c[j++];
    for(int k = 1; k <= cnt; k++) c[k + s1 - 1] = tmp[k];
}

void merge_sort(int l, int r)
{
    if(l >= r) return;
    int mid = (l + r) / 2;
    merge_sort(l, mid);
    merge_sort(mid + 1, r);
    merge(l, mid, mid + 1, r);
}

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++) 
    {
        cin >> a[i].value;
        a[i].idx = i;
    }
    sort(a + 1, a + n + 1, cmp_value);
    for(int i = 1; i <= n; i++) a[i].value = i; //把数值按顺序离散化处理
    
    for(int i = 1; i <= n; i++) h[a[i].value] = a[i].idx; //保存value-idx的映射关系

    for(int i = 1; i <= n; i++)
    {
        cin >> b[i].value;
        b[i].idx = i;
    } 
    sort(b + 1, b + n + 1, cmp_value);
    for(int i = 1; i <= n; i++) b[i].value = i; //把数值按顺序离散化处理
    sort(b + 1, b + n + 1, cmp_idx); //还原为原来的顺序
    for(int i = 1; i <= n; i++) c[i] = h[b[i].value]; //c数组是将b的value替换为同样数值在a中对应的idx

    //计算c中的逆序对
    merge_sort(1, n);
    cout << ans % MOD;

    return 0;
}

当然，计算逆序对也可以使用树状数组，代码更好写，参考：https://www.cnblogs.com/jcwy/p/18552254