洛谷题单指南-常见优化技巧-P1578 奶牛浴场

原题链接：https://www.luogu.com.cn/problem/P1578

题意解读：在有障碍点的矩形内找到一个最大矩形，内部不能包含障碍点，边缘可以包含障碍点。

解题思路：

求最大矩形的两种算法：极大矩形法、悬线法，背景知识阅读：浅谈用极大化思想解决最大子矩阵问题

关于悬线法，前面在玉蟾宫 题解中已有介绍。

先说结论：极大矩形法复杂度是O(s^2)，s是障碍点数量，悬线法复杂度是O(n*m)，n、m是矩形长、宽

根据不同的题目，可以选择不同的算法，一般来说，障碍点数量较少的情况，可以采用极大矩形法，而矩形长、宽不大的情况下可以

采用悬线法。

本题矩形长、宽为30000，而障碍点为5000，因此需采用极大矩形法。

枚举极大矩形的过程：

由于要覆盖边界的情况，可以直接将边界上的四个顶点也作为障碍点，一并处理。

先不考虑顶点的存在，假设有三个障碍点，排列位置如图

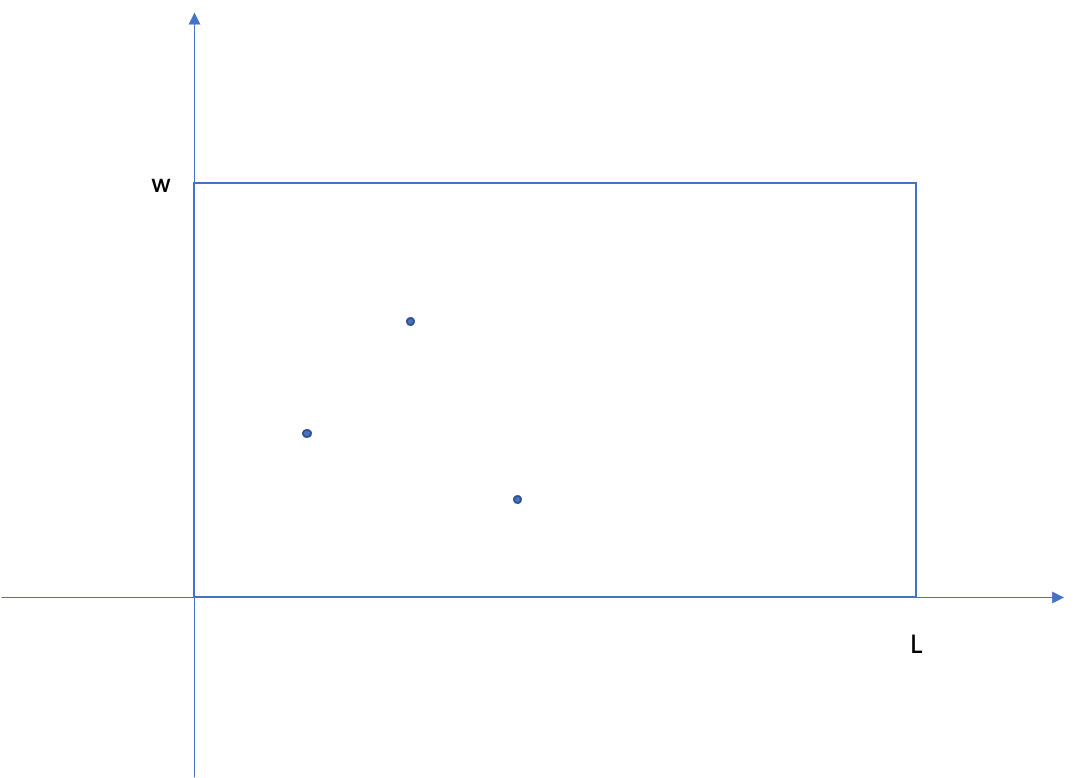
1、先对所有障碍点按x坐标排序，按水平从左到右依次处理各个障碍点

设极大矩形的左边x坐标为left，右边x坐标为right，上边y坐标为up，下边y坐标为down

对于第一个障碍点，有left = a[1].x，up=w，down=0

  当right = a[2].x时，极大矩形如图：

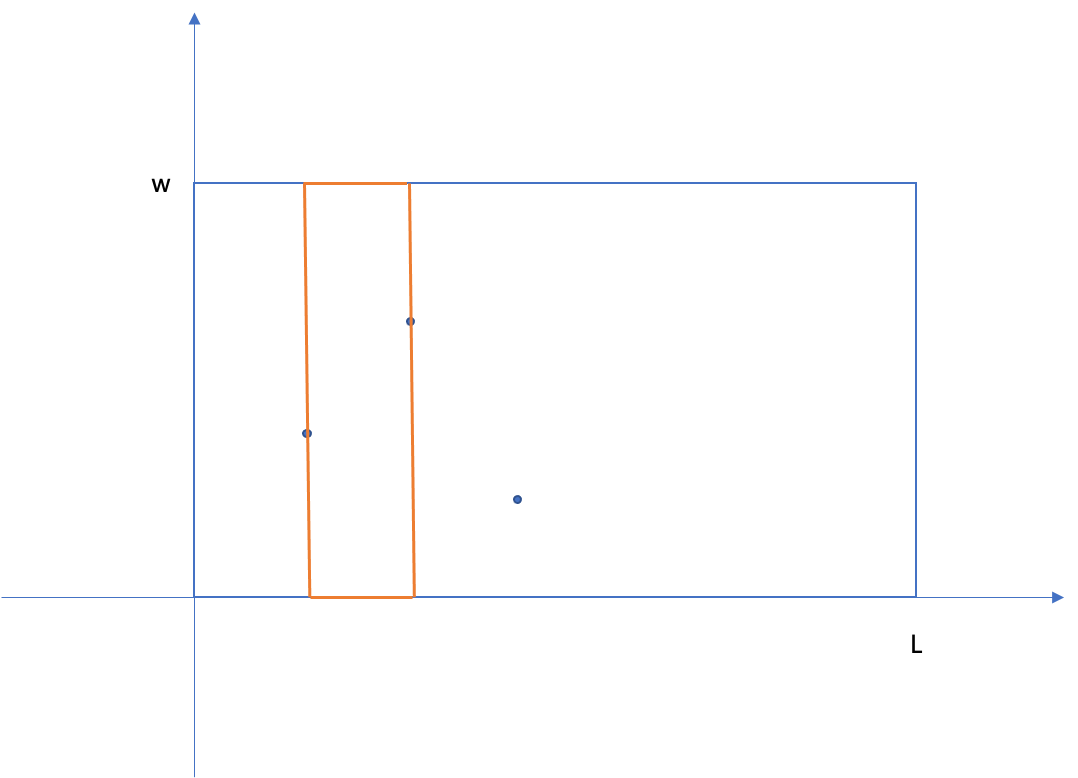
  在枚举right的位置为a[3].x前，需要更新up、down，由于a[2].y > a[1].y，因此up要更新为a[2].y

  当right = a[3].x时，极大矩形如图：

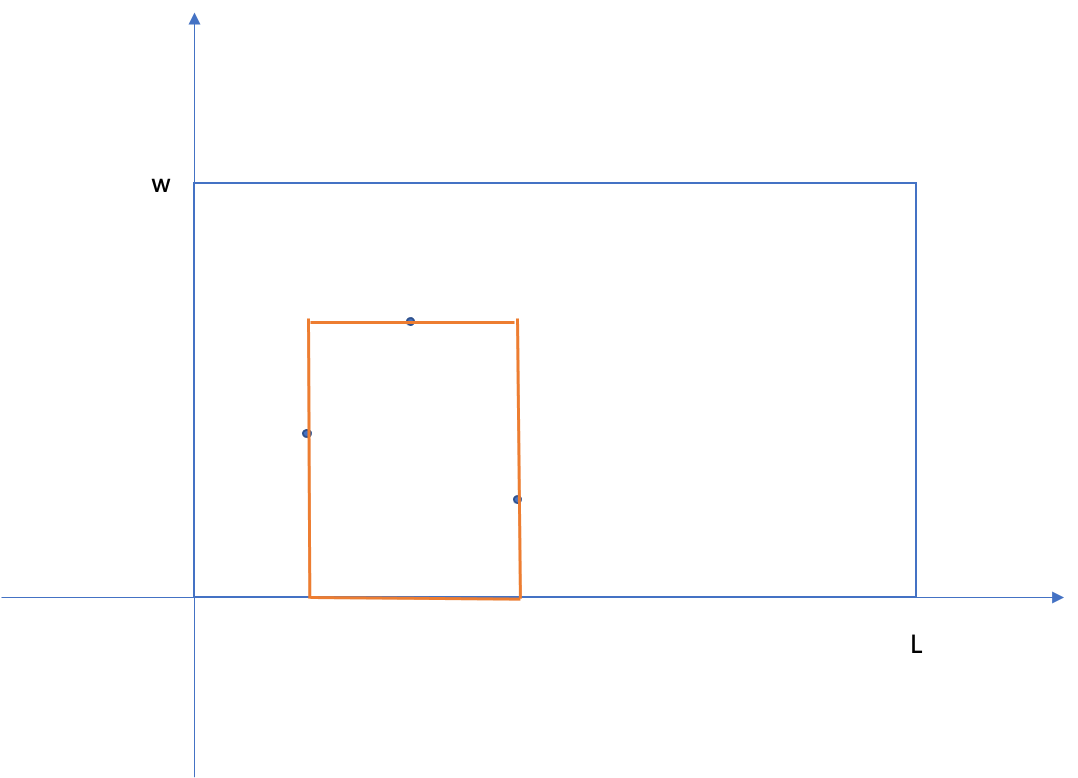
  再往后枚举障碍点，就要将down更新为down=a[3].y

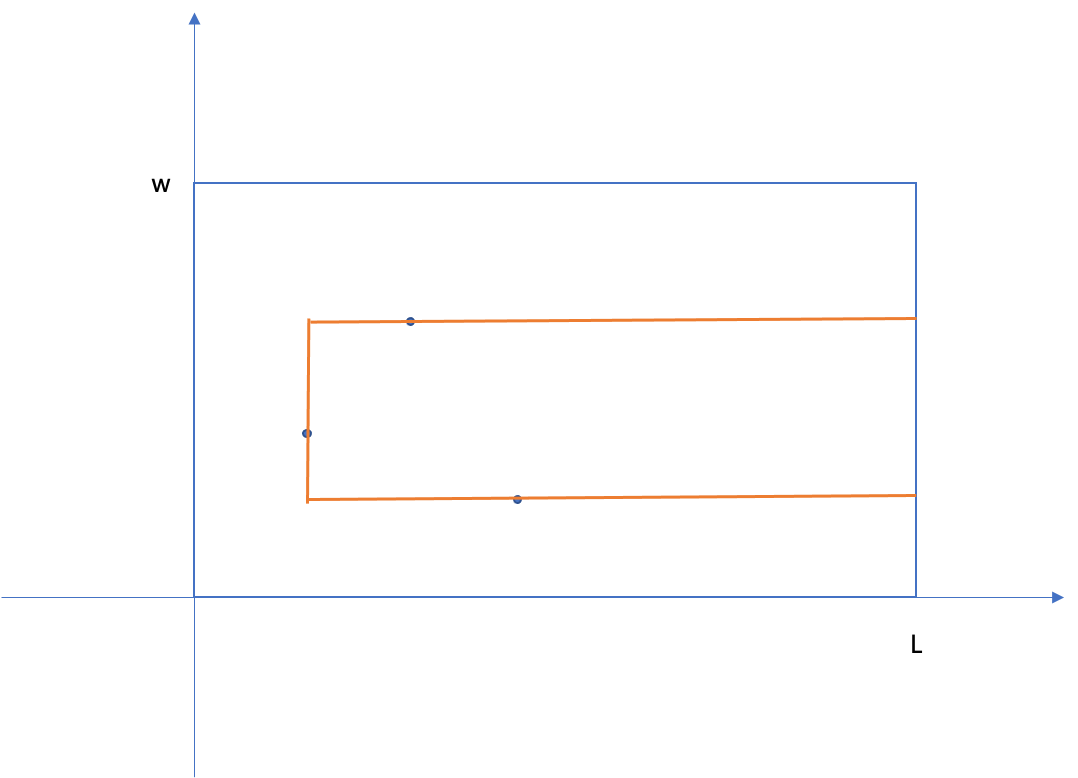
直到枚举完所有障碍点

2、再对所有障碍点按y坐标排序，按垂直从下到上依次处理各个障碍点

处理过程与水平方向类似，不重复过程，参考代码会更清晰。

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 5005;

int l, w, n, ans;
struct node 
{
    int x, y;
} a[N];

bool cmpx(node a, node b)
{
    return a.x < b.x;
}

bool cmpy(node a, node b)
{
    return a.y < b.y;
}

int main()
{
    cin >> l >> w >> n;
    for(int i = 1; i <= n; i++) cin >> a[i].x >> a[i].y;
    //将牛场4个顶点也加入障碍点一并处理
    a[++n].x = 0, a[n].y = 0;
    a[++n].x = 0, a[n].y = w;
    a[++n].x = l, a[n].y = 0;
    a[++n].x = l, a[n].y = w;

    int left = 0, right = 0, up = 0, down = 0;

    //水平处理
    sort(a + 1, a + n + 1, cmpx);
    for(int i = 1; i <= n; i++)
    {
        left = a[i].x;
        up = w, down = 0;
        for(int j = i + 1; j <= n; j++)
        {
            right = a[j].x;
            ans = max(ans, (right - left) * (up - down));
            if(a[j].y > a[i].y) up = min(up, a[j].y);
            else down = max(down, a[j].y);
        }
    }

    //垂直处理
    sort(a + 1, a + n + 1, cmpy);
    for(int i = 1; i <= n; i++)
    {
        down = a[i].y;
        left = 0, right = l;
        for(int j = i + 1; j <= n; j++)
        {
            up = a[j].y;
            ans = max(ans, (right - left) * (up - down));
            if(a[j].x > a[i].x) right = min(right, a[j].x);
            else left = max(left, a[j].x);
        }
    }

    cout << ans;
    return 0;
}