洛谷题单指南-常见优化技巧-P2216 [HAOI2007] 理想的正方形
原题链接:https://www.luogu.com.cn/problem/P2216
题意解读:在矩阵中找n*n正方形里最大值和最小值差值的最小值。
解题思路:
1、枚举法
直接枚举所有n*n的正方形的位置,然后在遍历求最大值、最小值,复杂度为O(n^4),显然不能通过。
2、二维单调队列
既然是求正方形范围内的最值,看起来是二维,其实可以转化为一维,过程如下:
一、先求n*n正方形范围的最大值:
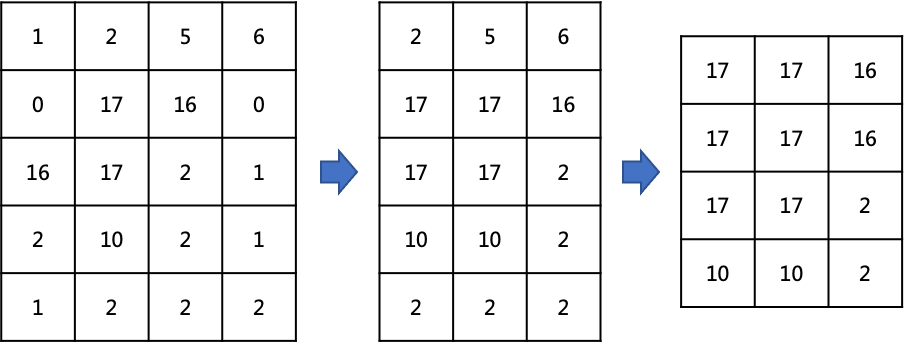
第一步:按行处理,计算每行滑动窗口长度是n范围的最大值
第二步:按列处理,计算每列滑动窗口长度是n范围的最大值
二、再求n*n正方形范围的最小值
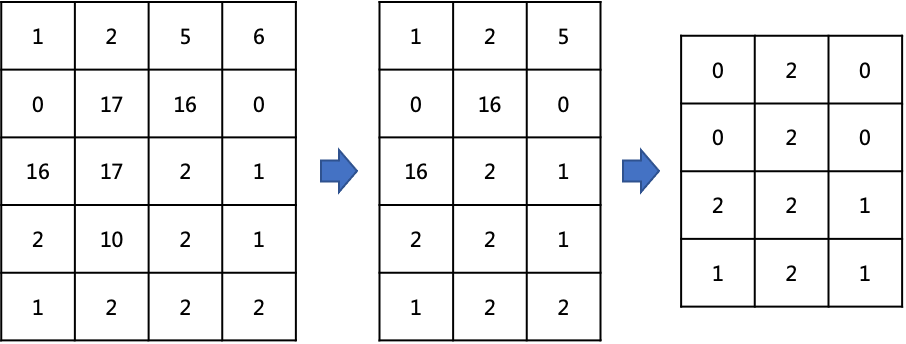
第一步:按行处理,计算每行滑动窗口长度是n范围的最小值
第二步:按列处理,计算每列滑动窗口长度是n范围的最小值
三、对上述过程计算求得的所有最大值、最小值对应的进行相减,取最小值,结果为1。
因此,该过程涉及4次单调队列求最值的应用。
100分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int a, b, n;
int w[N][N];
int xmax[N][N], xymax[N][N]; //行窗口最大值,列窗口最大值
int xmin[N][N], xymin[N][N]; //行窗口最小值,列窗口最小值
int q[N], l = 0, r = -1;
int main()
{
cin >> a >> b >> n;
for(int i = 1; i <= a; i++)
{
for(int j = 1; j <= b; j++)
{
cin >> w[i][j];
}
}
for(int i = 1; i <= a; i++)
{
l = 0, r = -1;
for(int j = 1; j <= b; j++)
{
while(l <= r && j - q[l] + 1 > n) l++;
while(l <= r && w[i][j] > w[i][q[r]]) r--;
q[++r] = j;
if(j >= n) xmax[i][j - n + 1] = w[i][q[l]];
}
}
for(int i = 1; i <= b - n + 1; i++)
{
l = 0, r = -1;
for(int j = 1; j <= a; j++)
{
while(l <= r && j - q[l] + 1 > n) l++;
while(l <= r && xmax[j][i] > xmax[q[r]][i]) r--;
q[++r] = j;
if(j >= n) xymax[j - n + 1][i] = xmax[q[l]][i];
}
}
for(int i = 1; i <= a; i++)
{
l = 0, r = -1;
for(int j = 1; j <= b; j++)
{
while(l <= r && j - q[l] + 1 > n) l++;
while(l <= r && w[i][j] < w[i][q[r]]) r--;
q[++r] = j;
if(j >= n) xmin[i][j - n + 1] = w[i][q[l]];
}
}
for(int i = 1; i <= b - n + 1; i++)
{
l = 0, r = -1;
for(int j = 1; j <= a; j++)
{
while(l <= r && j - q[l] + 1 > n) l++;
while(l <= r && xmin[j][i] < xmin[q[r]][i]) r--;
q[++r] = j;
if(j >= n) xymin[j - n + 1][i] = xmin[q[l]][i];
}
}
int ans = 2e9;
for(int i = 1; i <= a - n + 1; i++)
{
for(int j = 1; j <= b - n + 1; j++)
{
ans = min(ans, xymax[i][j] - xymin[i][j]);
}
}
cout << ans;
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识?