洛谷题单指南-前缀和差分与离散化-P1719 最大加权矩形

原题链接：https://www.luogu.com.cn/problem/P1719

题意解读：在n*n的矩阵中，找到和最大的子矩阵，求最大的子矩阵和。

解题思路：

1、暴力解法

第一步、枚举所有的子矩阵

可以通过枚举子矩阵的左上角(x1,y1)、右下角(x2,y2)来枚举所有子矩阵：

for(int x1 = 1; x1 <= n; x1++)
    for(int y1 = 1; y1 <= n; y1++)
        for(int x2 = x1; x2 <= n; x2++)
            for(int y2 = y1; y2 <= n; y2++)

算法时间复杂度大概是n^4 / 2

第二步、计算子矩阵的和，时间复杂度n^2

第三步、更新答案

综合看来，会超时，不可行。

2、二维前缀和

计算子矩阵的和可以借助于二维前缀和。

设s[N][N]是a[N][N]的前缀和数组

如上图，二维数组的每个格子表示a[i][j]，前缀和s[i][j]表示为从(1,1)到(i,j)的子矩阵所有格子的和

递推式：

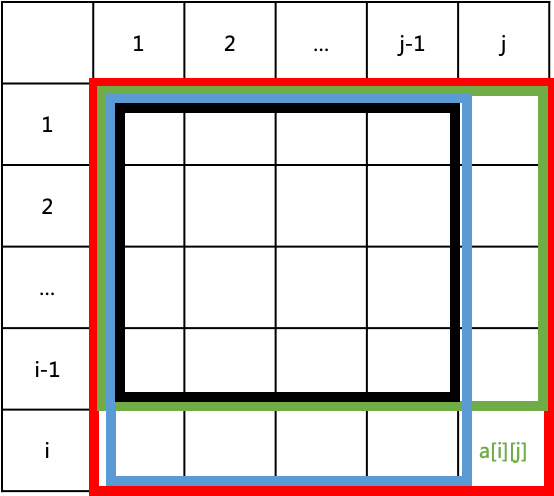
用红色区域表示s[i][j]，绿色区域表示s[i-1][j]，蓝色区域表示s[i][j-1]，黑色区域表示s[i-1][j-1]

则有s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j]

有了二维前缀和数组s[][]，可以用O(1)的复杂度求子矩阵的和：

如上图，要计算子矩阵(x1,y1)(x2,y2)的和，即红色区域

蓝色区域表示s[x2][y2]，黄色区域表示s[x1-1][y2]，绿色区域表示s[x2][y1-1]，黑色区域表示s[x1-1][y1-1]

则有子矩阵(x1,y1)(x2,y2)的和 = s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 125;

int n, ans = -1e9;
int a[N][N], s[N][N];

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
        {
            cin >> a[i][j];
            //计算前缀和
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
    
    //枚举所有子矩形：左上角(x1,y1)，右下角(x2,y2)
    for(int x1 = 1; x1 <= n; x1++)
        for(int y1 = 1; y1 <= n; y1++)
            for(int x2 = x1; x2 <= n; x2++)
                for(int y2 = y1; y2 <= n; y2++)
                {
                    //子矩形(x1,y1)(x2,y2)的和
                    int sum = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
                    ans = max(ans, sum);
                }

    cout << ans;

    return 0;
}