洛谷题单指南-动态规划2-P3147 [USACO16OPEN] 262144 P

原题链接：https://www.luogu.com.cn/problem/P3147

题意解读：将一组数据两两相邻且相同的合并，合并成一个数值+1的数，求合并后的最大值。

解题思路：

考虑合并后的最大数i，其最后一次必然是由两个i-1合并而来的

设dp[i][j]表示以j为左端点，合并最大值为i时的右端点的下一个位置

如图：

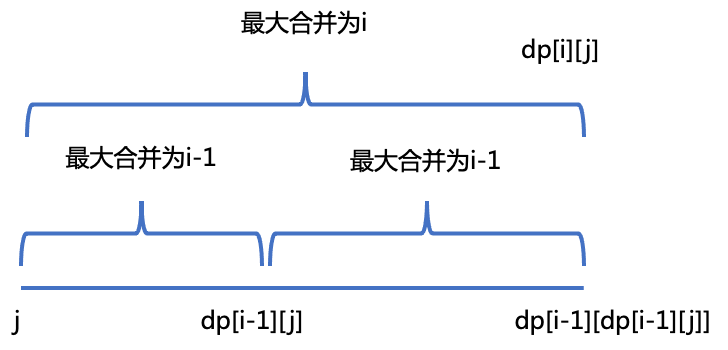
dp[i][j]可以拆解为两部分：

1、从j为左端点，最大合并为i-1的右端点的下一个位置，即dp[i-1][j]

2、从dp[i-1][j]为左端点，最大合并为i-1的右端点的下一个位置，即dp[i-1][dp[i-1][j]]

因此，状态转移为dp[i][j] = dp[i-1][dp[i-1][j]]

初始化：对于每一个数a[i]，有dp[a[i]][i] =i+1; //[i ~ i+1）最大可以合成a[i]

取值范围：

i的范围：如果262144个数全是40，最多合并次数是log2(262144)，最大值会到40+log2(262144) = 58

j的范围：1~262144

求值：枚举i，j，更新dp[i][j]，如果dp[i][j]不为0，则更新答案为i

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 262144;
const int M = 58; //如果262144个数全是40，最多合并次数是log2(262144)，最大值会到40+log2(262144) = 58
int n, ans;
int a[N];
int dp[M + 5][N + 5]; //dp[i][j]表示以j为左端点，合并最大值为i时的右端点的下一个位置

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        dp[a[i]][i] = i + 1; //[i ~ i+1）最大可以合成a[i]
    } 
    
    for(int i = 2; i <= M; i++)
    {
        for(int j = 1; j <= N; j++)
        {
            if(!dp[i][j]) dp[i][j] = dp[i-1][dp[i-1][j]];
            if(dp[i][j]) ans = i;
        }
    }
    cout << ans;
    return 0;
}