洛谷题单指南-图的基本应用-P1807 最长路
原题链接:https://www.luogu.com.cn/problem/P1807
题意解读:由于对于每一条边u->v,都有u < v,因此节点1的入度一定是0,且是有向无环图,直观上可以通过拓扑排序法搜索每一个节点,计算1到每一个节点的最长距离。但问题在于,入度为0的节点可能不止一个,这样在计算到某个点的最长距离时,会受到其他没有经过1的节点的影响,如下图:
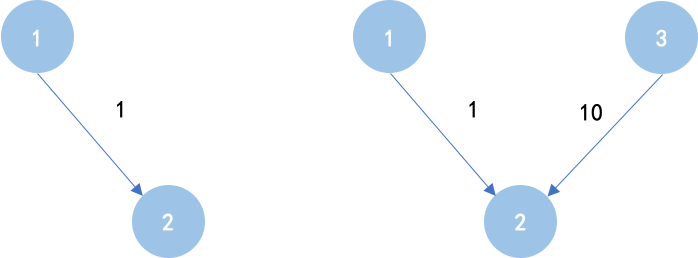
对于左边的情况,很明显,通过拓扑排序可以计算1到2的最长距离为1;
而对于右边的情况,拓扑排序时,先把1、3加入队列,根据1可以确定2的距离为1,根据3又可以把2的距离更新为10,答案就不对了,本质原因是因为3没有经过1,通过3来更新2的距离是不对的,需要想办法排除掉其他入度为0节点对最长距离计算造成的影响。
解题思路:
有两种办法来解决这个问题:
1、从非1的入度为0的节点开始,把他们能经过的所有节点的入度都减1,如果又产生了入度为0的节点,继续进行此操作,这样最终确保拓扑序只能从1开始,再正常使用拓扑排序法来计算1到每个节点的最长路径即可。
100分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1505;
struct node
{
int v, w;
};
vector<node> g[N];
queue<int> q;
int in[N]; //每个节点的入度
long long l[N]; //到每一个节点的最长路
int n, m, u, v, w;
bool bfs()
{
bool success = false;
for(int i = 1; i <= n; i++) l[i] = -1e10; //l数组元素初始化为负无穷,便于后面的max比较
l[1] = 0; //节点1的距离是0
q.push(1); //从1开始进行拓扑排序
while(q.size())
{
int u = q.front(); q.pop();
for(int i = 0; i < g[u].size(); i++)
{
int v = g[u][i].v, w = g[u][i].w;
if(--in[v] == 0) q.push(v);
l[v] = max(l[v], l[u] + w); //到v节点的最长路等于所有到v的路径长度中的最大值
if(v == n) success = true; //找到节点n,并且是经过1的
}
}
return success;
}
int main()
{
cin >> n >> m;
while(m--)
{
cin >> u >> v >> w;
g[u].push_back({v, w});
in[v]++;
}
//去除非1入度为0的节点影响
for(int i = 1; i <= n; i++)
{
if(i != 1 && in[i] == 0)
{
q.push(i);
}
}
while(q.size())
{
int u = q.front(); q.pop();
for(int i = 0; i < g[u].size(); i++)
{
int v = g[u][i].v;
if(--in[v] == 0) q.push(v);
}
}
//从1开始进行拓扑排序,计算每个节点到1的最长距离
bool res = bfs();
if(res) cout << l[n];
else cout << -1;
return 0;
}2、不必排除掉所有非1的入度为0的节点,正常使用拓扑排序法,要把搜索到的每个点是否经过了1进行标记,只有经过了1到达的点,才进行距离的更新。
100分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1505;
struct node
{
int v, w;
};
vector<node> g[N];
queue<int> q;
int in[N]; //每个节点的入度
long long l[N]; //到每一个节点的最长路
bool from1[N]; //每个节点是否是经过1来的
int n, m, u, v, w;
bool bfs()
{
bool success = false;
from1[1] = true;
for(int i = 1; i <= n; i++) l[i] = -1e10; //l数组元素初始化为负无穷,便于后面的max比较
l[1] = 0; //节点1的距离是0
for(int i = 1; i <= n; i++)
{
if(in[i] == 0)
{
q.push(i);
}
}
while(q.size())
{
int u = q.front(); q.pop();
for(int i = 0; i < g[u].size(); i++)
{
int v = g[u][i].v, w = g[u][i].w;
if(--in[v] == 0) q.push(v);
if(from1[u]) //只考虑能从1过来的情况,不经过1的不用考虑
{
l[v] = max(l[v], l[u] + w); //到v节点的最长路等于所有从1能到v的路径长度中的最大值
from1[v] = true; //如果前置节点u是从1来的,v也是从1来的
if(v == n) success = true; //找到节点n,并且是经过1的
}
}
}
return success;
}
int main()
{
cin >> n >> m;
while(m--)
{
cin >> u >> v >> w;
g[u].push_back({v, w});
in[v]++;
}
bool res = bfs();
if(res) cout << l[n];
else cout << -1;
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】