洛谷题单指南-图的基本应用-P4017 最大食物链计数

原题链接：https://www.luogu.com.cn/problem/P4017

题意解读：食物链的顶端不会被其他生物吃，在图结构中设定为入度是0，食物链的底端不会吃其他生物，在图结构中设定为出度是0，此题就是要计算所有入度是0的点到所有出度是0的点一共有多条路径。

解题思路：

首先，来模拟样例，样例数据形成的图如下：

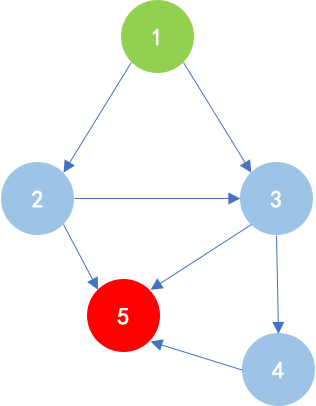
在此图中，食物链的顶端是1，食物链的底端是5，要求1->5的所有路径数，其实就是求有多少条路可以到达5

设数组l[N]为顶端到每个节点的路径条数

节点5可以从2、3、4过来，因此l[5] = l[2] + l[3] + l[4]

节点2可以从1过来，l[2] = l[1]，节点1的路径数就是1，l[1] = 1，所以l[2] = 1

节点3可以从1、2过来，l[3] = l[2] + l[1] = 1 + 1 = 2

节点4可以从3过来，l[4] = l[3] = 2

所以l[5] = 1 + 2 + 2 = 5

以上过程，其实本质上，就是计算到每个节点的路径条数。

在拓扑排序的过程中，会先搜索完某个节点所有的前置节点，这个过程就可以计算到这个节点的路径数，等于到所有前置节点路径数之和，

到所有顶端节点（入度为0）的路径数都初始化为1即可，

另外，注意底端节点可能有多个，要把到所有出度为0的节点路径数加起来。

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 5005;
const int MOD = 80112002;

vector<int> g[N];
queue<int> q;
int in[N], out[N]; //入度、出度
int l[N]; //到每个节点的路径条数
int n, m, a, b;
int ans;

void bfs()
{
    for(int i = 1; i <= n; i++)
    {
        if(in[i] == 0)
        {
            q.push(i);
            l[i] = 1; //到入度为0的节点的路径数是1
        }
    }
    while(q.size())
    {
        int u = q.front(); q.pop();
        for(int i = 0; i < g[u].size(); i++)
        {
            int v = g[u][i];
            if(--in[v] == 0) q.push(v);
            l[v] = (l[v] + l[u]) % MOD; //到v的路径条数就是到所有前置节点的路径条数之和
        }
    }
}

int main()
{
    cin >> n >> m;
    while(m--)
    {
        cin >> a >> b;
        g[b].push_back(a);
        in[a]++; //记录入度
        out[b]++; //记录出度
    }
    bfs();
    for(int i = 1; i <= n; i++)
    {
        if(out[i] == 0)
        {
            ans = (ans + l[i]) % MOD; //计算到所有出度为0的节点的路径数之和
        }
    }
    cout << ans;

    return 0;
}