洛谷题单指南-递推与递归-P1228 地毯填补问题
原题链接:https://www.luogu.com.cn/problem/P1228
题意解读:用4种毯子铺满2^k * 2^k的区域,留出一个公主位置,输出所有毯子拐角的坐标以及哪种毯子,看起来有点无从下手,
可以从k=1,k=2,k=3入手去依次考虑,找到规律,用分治法解决。
解题思路:
1、当k=1时,即2*2的区域,对于任意一个位置是公主,都可以得到唯一一种铺设方案

2、当k=2时,即4*4的区域,对于任意一个位置是公主,如下图:
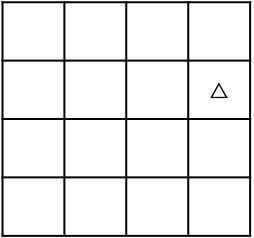
可以将4*4区域划分成4个2*2的区域
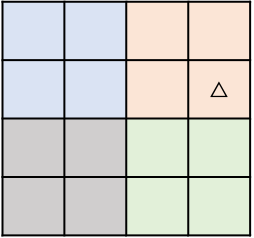
如果每个区域都有一个公主,问题就好解决了,因为右上区域有了公主,可以假设最中间的2*2区域的右上角有公主,先对这个区域进行铺设:

然后,把中间铺设的地毯都当做公主,这样就能保证4个2*2的区域都有了公主:

再分4个区域依次进行处理,问题就变成了k=1时的情况,即可得到上图的结果。
3、同理,当k=3时,即8*8的区域,对于任意位置是公主,如下图:

将8*8区域划分成4个4*4区域
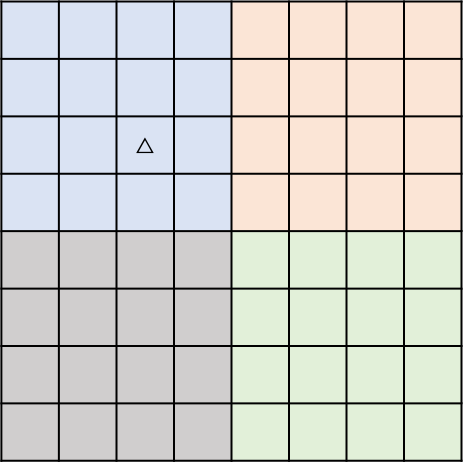
根据公主所在的区域,对中间2*2区域进行铺设
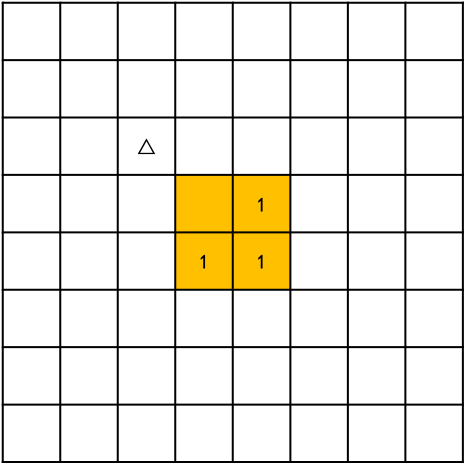
这样,假设中间2*2铺设的毯子都是公主,则4个4*4区域就都有了公主

再依次对4个4*4区域进行处理,问题就变成了k=2时的情况,最终可以变成k=1时的情况,问题得解。
100分代码:
#include <bits/stdc++.h>
using namespace std;
int k, x, y;
//cover是铺地毯函数,(x1,y1)是左上角的坐标,(x2,y2)是右下角的坐标,(x,y)是公主的的坐标
void cover(int x1, int y1, int x2, int y2, int x, int y)
{
if(x2 - x1 == 1) //2 * 2区域时
{
//公主在左上角,用毯子1
if(x1 == x && y1 == y) cout << x2 << " " << y2 << " " << 1 << endl;
//公主在右上角,用毯子2
else if(x1 == x && y2 == y) cout << x2 << " " << y1 << " " << 2 << endl;
//公主在左下角,用毯子3
else if(x2 == x && y1 == y) cout << x1 << " " << y2 << " " << 3 << endl;
//公主在右下角,用毯子4
else cout << x1 << " " << y1 << " " << 4 << endl;
return;
}
//将2^k * 2^k区域分成4个2^(k-1) * 2^(k-1)的区域
//计算公主在哪个区域,把正中间的2*2区域用一个地毯覆盖,这个地毯相当于让4个2^(k-1) * 2^(k-1)的区域都有一个公主
//再递归处理
int len = x2 - x1 + 1; //len是边长
int half = len / 2; //half是边长的一半
//中间2 * 2区域每个格子的坐标
int xa = x1 + half - 1, ya = y1 + half - 1; //左上
int xb = x1 + half - 1, yb = y1 + half; //右上
int xc = x1 + half, yc = y1 + half - 1; //左下
int xd = x1 + half, yd = y1 + half; //右下
//公主在左上区域
if(x >= x1 && x <= xa && y >= y1 && y <= ya)
{
//填补正中间2*2区域
cover(xa, ya, xd, yd, xa, ya);
//设定左上区域的公主位置
xa = x, ya = y;
}
//公主在右上区域
else if(x >= x1 && x <= xb && y >= yb && y <= y2)
{
//填补正中间2*2区域
cover(xa, ya, xd, yd, xb, yb);
//设定右上区域的公主位置
xb = x, yb = y;
}
//公主在左下区域
else if(x >= xc && x <= x2 && y >= y1 && y <= yc)
{
//填补正中间2*2区域
cover(xa, ya, xd, yd, xc, yc);
//设定左下区域的公主位置
xc = x, yc = y;
}
//公主在右下区域
else
{
//填补正中间2*2区域
cover(xa, ya, xd, yd, xd, yd);
//设定右下区域的公主位置
xd = x, yd = y;
}
//递归处理4个2^(k-1) * 2^(k-1)的区域
cover(x1, y1, x1 + half - 1, y1 + half - 1, xa, ya); //左上
cover(x1, y1 + half, x1 + half - 1, y2, xb, yb); //右上
cover(x1 + half, y1, x2, y1 + half - 1, xc, yc); //左下
cover(x1 + half, y1 + half, x2, y2, xd, yd); //右下
}
int main()
{
cin >> k >> x >> y;
cover(1, 1, 1 << k, 1 << k, x, y);
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 如何调用 DeepSeek 的自然语言处理 API 接口并集成到在线客服系统
· 【译】Visual Studio 中新的强大生产力特性
· 2025年我用 Compose 写了一个 Todo App