洛谷题单指南-模拟和高精度-P4924 [1007] 魔法少女小Scarlet

原题链接：https://www.luogu.com.cn/problem/P4924

题意解读：

根据题意，通过模拟法，枚举每一个要旋转的矩阵，执行旋转操作即可，关键点在于如何进行矩阵旋转。

设定矩阵int a[][]， 临时矩阵int t[][]用于保存旋转后的矩阵，矩阵长度为len。

先考虑要旋转的区域左上角是a[0][0]的情况，区域内每个元素下标值是i，j，i∈[0, len-1]，j∈[0, len-1]。

1、顺时针旋转90度：

先以行的角度看坐标如何变换：

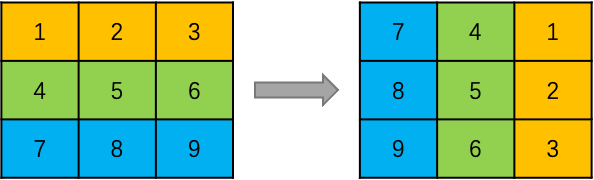
可以看出，行号经过顺时针旋转90度后，变成了反向的列号。

再以列的角度看坐标如何变换：

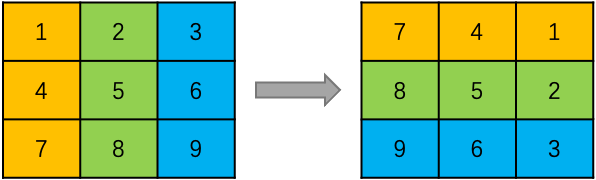
可以看出，列号经过顺时针旋转90度后，变成了行号。

因此，对int a[i][j]执行顺时针旋转的操作，保存到int t[][]中，为

t[j][len - i - 1] = a[i][j]（行号i变成了反向的列号len - i - 1，列号j变成了行号）

如果旋转的区域左上角不是a[0][0]，而是a[x][y]，变换时行+x，列+y即可，为

t[x + j][y + len - i - 1] = a[x + i][y + j]

2、逆时针旋转90度：

先以行的角度看坐标如何变换：

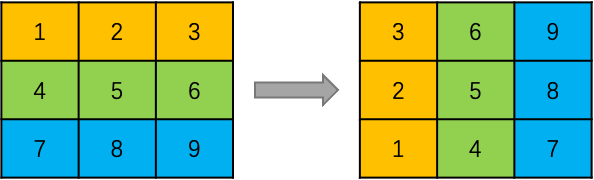
可以看出，行号经过顺时针旋转90度后，变成了列号。

再以列的角度看坐标如何变换：

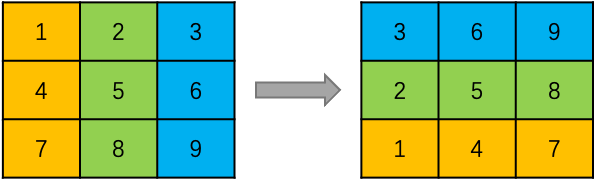
可以看出，列号经过顺时针旋转90度后，变成了反向的行号。

因此，对int a[i][j]执行逆时针旋转的操作，保存到int t[][]中，为

t[len - j - 1][i] = a[i][j]（行号i变成了列号，列号j变成了反向的行号len - j - 1）

如果旋转的区域左上角不是a[0][0]，而是a[x][y]，变换时行+x，列+y即可，为

t[x + len - j - 1][y + i] = a[x + i][y + j]

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 505;

int a[N][N], t[N][N];
int n, m;

//将左上角是x，y，边长len的矩形旋转90度，z=0顺时针，z=1逆时针
void rotate(int x, int y, int len, int z)
{
    for(int i = 0; i < len; i++)
        for(int j = 0; j < len; j++)
            if(z == 0) t[x + j][y + len - i - 1] = a[x + i][y + j];  
            else t[x + len - j - 1][y + i] = a[x + i][y + j];
            
    for(int i = 0; i < len; i++)
        for(int j = 0; j < len; j++)    
            a[x + i][y + j] = t[x + i][y + j];
}

int main()
{
    cin >> n >> m;

    //初始化
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++) 
            a[i][j] = (i - 1) * n + j;

    int x, y, r, z;
    //执行魔法
    for(int i = 1; i <= m; i++)
    {
        cin >> x >> y >> r >> z;
        int dx = x - r; //待旋转的矩形区域左上角x坐标
        int dy = y - r; //待旋转的矩形区域左上角y坐标
        int l = 2 * r + 1; //待旋转的矩形区域边长
        rotate(dx, dy, l, z); //旋转90度
    }        
    //输出结果
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= n; j++) cout << a[i][j] << " ";
        cout << endl;
    }

    return 0;
}