N皇后问题的一种解法
本文转载自:https://xie.infoq.cn/article/3d5174941484a82784d85624a
之前网上看到很多关于N皇后问题的解法,大都比较难懂也不易记住,今天分享下比较易懂的一个解法:

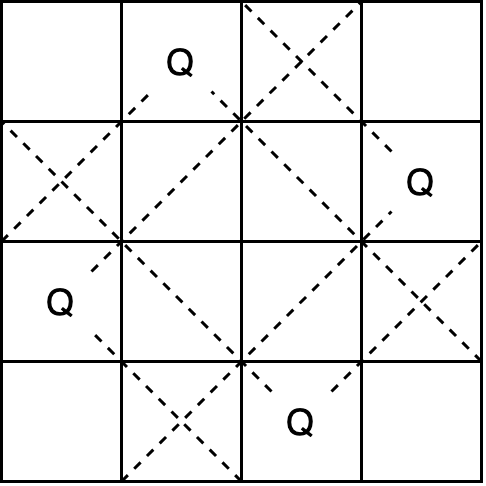
我们定义要求如下,给定一个n*n方格的棋盘,每一行放一个皇后,要求满足任一皇后所在的列及斜边上都不能有其他皇后存在,然后将所有解法打印出来,要求打印出n*n的字符矩阵,皇后的位置用“Q”表示,空格用“.”表示。拿4皇后来说,其中一个解如下图,需要满足的要求是行、列、斜边上都不能有其他皇后存在。
理解了题目要求后,现在分析题目的解法。要求给出所有可能的解,需要从第一行开始,逐行、逐列求解满足要求的行与列的序号,记录下符合的解,最后按格式输出。而每一次的判断都需要依赖之前合法的皇后放置结果,第i+1行所有列执行判断后,需要回到第i行,继续第i行下一列的判断,一个完整的解为当已经判断到最后一行,而此时最后一行的第j列符合要求,则此时的记录中为一个合法的解。直到所有行所有列的情况都判断完成,求解结束。所以这个问题适合用深度优先遍历的方式来解,从首行首列开始,优先向深度方向即向下一行搜索,下一行则遍历各列,找到第一个符合要求的列后即再向下一行也就是深度方向搜索……
用伪代码表示过程大致如下:
dfs (row) {
if (row == n) {
printOneSolver()
return;
}
for (col in n) {
if (valid(row, col) {
addToValidConditions(row, col)
dfs(row + 1)
removeFromValidConditions(row, col)
}
}
}
//说明:这里的row和col表明是与行列有关,真正的参数由行列引申而来。
上述伪码描述了大致的过程,便于整体上理解思路,接下来介绍如何判断合法性。先说行的判断,因为每行只能放置一个皇后,又是以行为深度向下遍历,所以一个合法的解其实只需要有n个列值信息就可以表示,比如其中一个合法解的列值为[1, 3, 0, 2](0表示第一列),这个解表示皇后放在第1行第2列,第2行第4列,第3行第1列,第4行第3列,因此行信息是不需要单独列出的。这个时候得出一个关键数据,就是用一个有序的数据结构来表示列,序号即为所在行,而该序号下的值为所在列,这个结构我们称为cols。
行不需要单独判断,而列有了如上数据结构表示,那就剩下斜边的判断了,画个图来说明一下斜边的判断如何做。
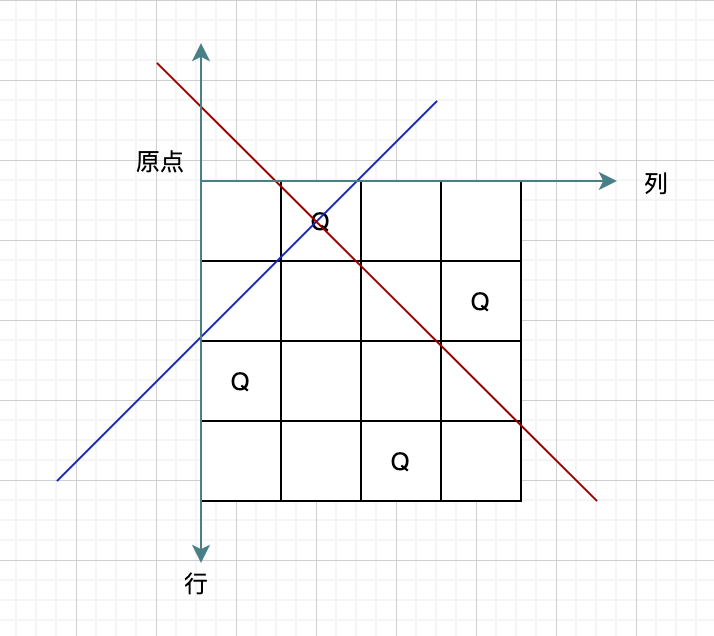
以左上角为坐标原点,向下表示行,向右表示列,从图上可以看到两个斜边其实是斜率为1和-1的两条直线,而在不同的皇后位置的斜边表示都是x+y=a和x-y=b的形式,a和b其实也就是截距,x和y就是行、列值,因此我们可以借助两个数据结构分别表示目前已经被占用的斜边,x+y的形式我们称为xySum,而x-y的形式,我们就称为xyDiff。
到目前我们得出合法的判断条件就是当前列不在cols中且行列之和不在xySum中且行列之差不在xyDiff中。这里需要注意一点,当合法时要将条件放入这几个结构,进行dfs,而dfs结束后,要还原为之前的状态,以便进行下一列的判断,这在伪代码中也有说明。
最后说下结果的打印,按要求的方式打印时我们仍以其中一个解为例来说明,[1, 3, 0, 2],对于该解其打印结果应为:
.Q.. ...Q Q... ..Q.
这里给出列序号如何拼接该行的输出,如当前列值为1,则表示皇后在第2列(列号从0开始),那么在皇后之前就有1个“.”,然后是“Q”,再然后是n-列序号-1个“.”,用公式表示如下,col代表列序号:
".".repeat(col) + "Q" + ".".repeat(n - col - 1)
为了输出后对于我们观察更直观,我们在字符后多加个空格,会更方便观察,所以改为如下公式:
". ".repeat(col) + "Q " + ". ".repeat(n - col - 1) //输出相应如下 . Q . . . . . Q Q . . . . . Q .
最后给出完整实现:
public void solveNQueens(int n) {
dfs(n, new ArrayList<>(), new HashSet<>(), new HashSet<>());
}
/**
* @param n 棋盘大小,也是皇后的数量
* @param cols 存放当前合法的列序号,其size的大小表示当前已经遍历的行数
* 而其值正好是要进行遍历的下一行
* @param xySum 行列之和,用Set存放
* @param xyDiff 行列之差,用Set存放
*/
private void dfs(int n, List<Integer> cols, Set<Integer> xySum, Set<Integer> xyDiff) {
//当cols.size为n时,表明每一行都可以合法放置一个皇后,得到一个合法解
if (cols.size() >= n) {
printOneSolver(cols);
return;
}
int row = cols.size();
for (int col = 0; col < n; col++) {
if (!cols.contains(col)
&& !xySum.contains(row + col)
&& !xyDiff.contains(row - col)) {
cols.add(col);
xySum.add(row + col);
xyDiff.add(row - col);
dfs(n, cols, xySum, xyDiff);
cols.remove(Integer.valueOf(col));
xySum.remove(Integer.valueOf(row + col));
xyDiff.remove(Integer.valueOf(row - col));
}
}
}
private void printOneSolver(List<Integer> cols) {
for (int i = 0; i < cols.size(); i++) {
System.out.println(". ".repeat(cols.get(i))
+ "Q "
+ ". ".repeat(cols.size() - cols.get(i) - 1));
}
System.out.println();
}
以4皇后为例,输出如下:
. Q . . . . . Q Q . . . . . Q . . . Q . Q . . . . . . Q . Q . .
思路是这样,如果更换数据结构和判断的具体写法,效率上可能会高一点。之前也有看过说N皇后问题用位运算解决会更高效,位运算的解法完成之后将作为相关主题补充在文章末尾。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号