Resource and Performance Tradeoffs in Delay-Tolerant Wireless Networks
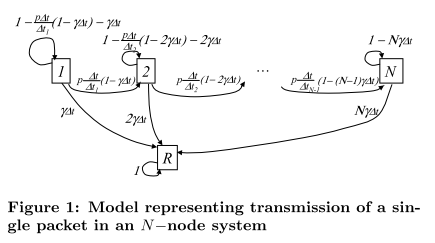
This Markov model assumes that node-to-node encounters and node-to-station encounters occur at exponentially distributed intervals and that all nodes have the same prob- ability of reaching a relay or a destination. This is a reasonable assumption for a sensor network with mobile nodes whose motion is independent from the location of the data- collecting stations. For example, consider a network of tags on animals where the animals are foraging for food. Each node independently follows a pseudo-random pattern and is equally likely to meet another node or station in its area at any time.
Finding the probability of the system in the state R as a function of time provides us with the cumulative distribution function for the delays of the packets, F(T). (即:消息的传输时延T就是系统进入状态R所花费的时间)
The energy consumption of the system is calculated by recording the number of transitions between states in this model. The system storage at timestep T, for a unique packet and its copies is found by adding up the probabilities of the different states multiplied by the number of packet copies in those states.
From the cumulative distribution of the delay, we are able to determine the threshold probability Pthresh that represents the confidence with which we desire each packet to be successfully offloaded to a collection station. For example, if Pthresh = 0.5 and F−1(0.5) = 200, then the packets need to remain in the system for 200 time-steps, after which time they are successfully offloaded with probability 0.5, and all the copies could (and should) then be removed from the system.


