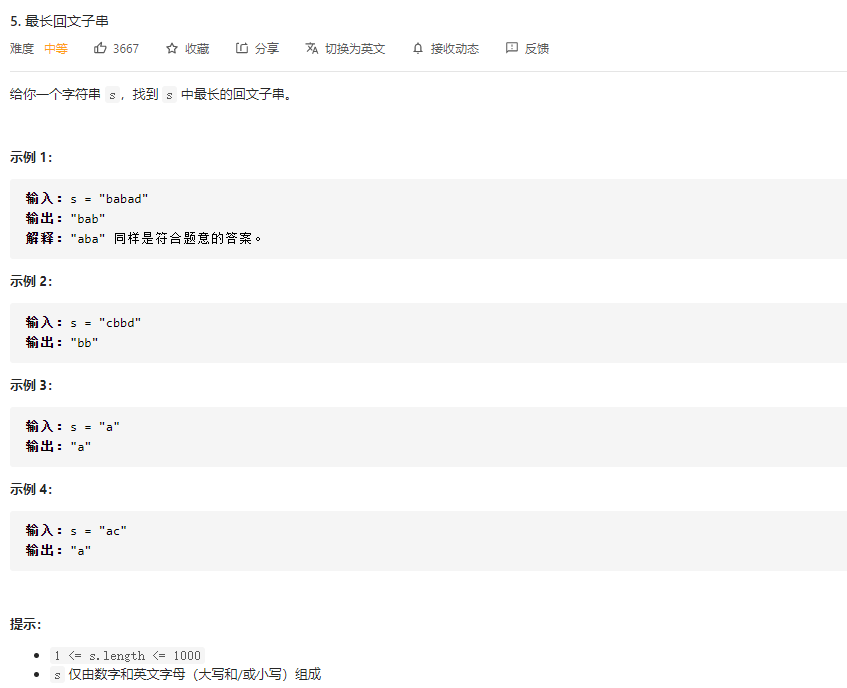
5. 最长回文子串

 

 

方法一、DP

假设dp[i][j]表示从i到j下标是否是回文串

于是有dp[i][j]=dp[i+1][j-1]^（s[i]==s[j]）

时间O(n^2)，空间O(n^2)

    public String longestPalindrome(String s) {
        int len = s.length();
        if(len<2){
            return s;
        }
        
        boolean dp[][] = new boolean[len][len];
        // 每个字符自身都是回文的
        for(int i=0;i<len;i++){
            dp[i][i]=true;
        }
        // 由于每个字符自身回文，因此最短也是1
        int maxLen = 1,begin=0;
        for(int j=1;j<len;j++){
            for(int i=0;i<j;i++){
                // 首尾不相等，则必然不回文
                if(s.charAt(i)!=s.charAt(j)){
                    dp[i][j]=false;
                }else{
                    // 首尾相同的情况下，前后相差位数不超过2的时候，必然是回文的
                    if(j-i<3){
                        dp[i][j]=true;
                    }else{
                        // 这里可以由之前的状态获取到当前的状态
                        dp[i][j]=dp[i+1][j-1];
                    }
                }
                // 每次循环后更新最长回文子串的长度与起始位置
                 if(dp[i][j]==true && (j-i+1)>maxLen){
                    maxLen = j-i+1;
                    begin = i;
                }              
            }           
        }
        return s.substring(begin,begin+maxLen);
    }

 

方法二、中心拓展

针对每个元素，我们以此为中心，使用双指针法向两边拓展。

直到不回文为止，每次结束更新最长回文子串的长度与起始位置

时间O(n^2)，空间O(1)

class Solution {
    public String longestPalindrome(String s) {
        int len=s.length();
        if(len<2){
            return s;
        }

        int start=0,end=0;
        for(int i=0;i<len;i++){
            // 需要考虑奇数和偶数2种情况
            int len_odd = expandCenter(s,i,i);
            int len_even = expandCenter(s,i,i+1);
            int maxLen = Math.max(len_odd,len_even);
            if(maxLen>end-start){
                start = i-(maxLen-1)/2;
                end = i+maxLen/2;
            }           
        }
        return s.substring(start,end+1);
    }

    public int expandCenter(String s,int left,int right){
        while(left>=0 && right<s.length() && s.charAt(left)==s.charAt(right)){
            left--;
            right++;
        }
        // 这里由于最后一次循环时start和end分别做了加减，所以是end-start-1+2=start-left-1
        return right-left-1;
    }
}

 

方法三、马拉车