leetcode刷题周记【2020.9.21-2020.9.26】

题目1. 两数之和

 

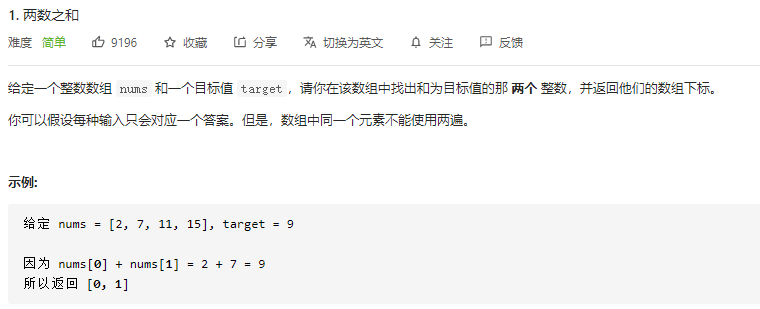
方法1，暴力求解，2层循环，时间复杂度O(n^2)，空间复杂度O(1)

   public int[] twoSum(int[] nums, int target) {
        int[] res = new int[2];
        for(int i=0;i<nums.length;i++){
            for(int j=i+1;j<nums.length;j++){
                if((nums[j]+nums[i]) == target){
                    res[0]=i;
                    res[1]=j;
                    return res;
                }
            }            
        }
        throw new IllegalArgumentException("No two sum solution");
    }

大多数人都能直接想到的办法，但是有没有办法“高大上”一点呢

方法2，使用map，“一次遍历”

我们知道map能够提供一种key-value的对应关系，当我们确定了
target以及组成target中的一个元素的时候，便有了target-nums[i]与nums[j]
之间的对应关系了，于是我们就有了

public int[] twoSum(int[] nums, int target) {
        int[] res = new int[2];
        HashMap<Integer,Integer> map = new HashMap<Integer,Integer>();
        for(int i=0;i<nums.length;i++){    
            map.put(nums[i],i);
            if(map.get(target-nums[i]) != null && map.get(target-nums[i])!=i) {
                res[0]=map.get(target-nums[i]);
                res[1]=i;
                return res;
            }
            
        }
        throw new IllegalArgumentException("No two sum solution");
    }

 

但是这里有一个问题，我们知道map的key是不能重复的，这里出现了
一种特殊情况需要考虑，那就是当两个值相同的元素出现时，这里的
map就会异常，如下图。

所以我们这里需要把put操作放在下面，以防这种特殊情况，同时我们再对
以上的代码做下优化，比如if判断的条件可以改为map.containsKey，并
在return时直接new一个数组，不在单独初始化一个。便有了如下AC代码：

public int[] twoSum(int[] nums, int target) {
        int[] res = new int[2];
        for(int i=0;i<nums.length;i++){
            for(int j=i+1;j<nums.length;j++){
                if((nums[j]+nums[i]) == target){
                    res[0]=i;
                    res[1]=j;
                    return res;
                }
            }            
        }
        throw new IllegalArgumentException("No two sum solution");
    }

最后，我来解释下为什么上面的“高大上”和“一次遍历”是带引号的，
表面上我们利用的map的属性，get和containskey简化了我们的代码，
但熟悉map的朋友都知道，这两个轮子实际上是通过map内部的
getNode来实现的，其内部使用了while循环来实现，所以事实上
我们的代码在时间复杂度上还是O(n^2)，并且你还消耗了一定的
建立map的哈希结构的时间。这就告诉我们，不是用了轮子就代表了
高效率，一方面要了解轮子，一方面要具体问题具体分析，灵活运用

题目7. 整数反转

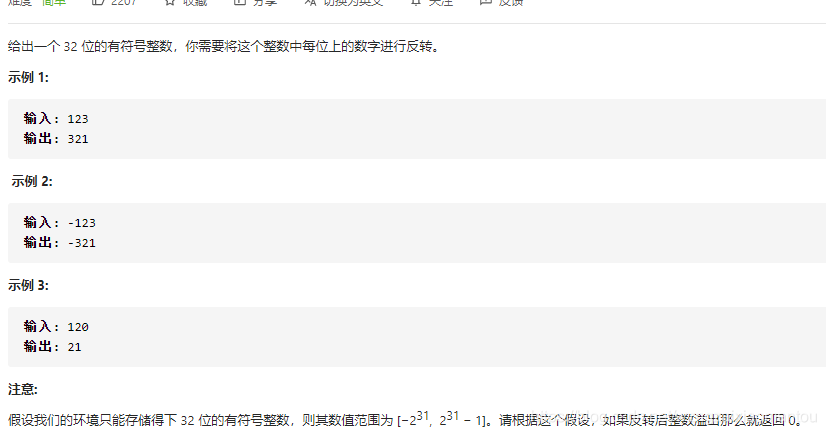
如果数据范围给的比较宽松的话，使用stringBuilder
的reverse这个轮子也是可以的，但是这里做出了限制
，为防止溢出问题使用数学的方法处理

具体的防溢出判断可以看LeetCode上大佬的思路，这里不献丑了
在不考虑溢出问题的情况下，简单归纳下就是，我们可以通过不停的
取模与取余的操作来获取到一个n位数的每一位数字，有了这些，
我们就能实现将他翻转。比如123这个数字，利用while循环我依次
去除了1，2，3，再在while内部使用((3*10)+2)*10+1便可轻松解决，
时间复杂度为O(n)（n为int数值x的长度）

public int reverse(int x) {
        int ans = 0;
        while (x != 0) {
            int pop = x % 10;
            if (ans > Integer.MAX_VALUE / 10 || (ans == Integer.MAX_VALUE / 10 && pop > 7)) 
                return 0;
            if (ans < Integer.MIN_VALUE / 10 || (ans == Integer.MIN_VALUE / 10 && pop < -8)) 
                return 0;
            ans = ans * 10 + pop;
            x /= 10;
        }
        return ans;
    }    

 

题目9. 回文数

不使用reverse这个轮子，那就还是用数学方法来解决，
首先根据题干给的例子，负数pass，然后末尾为0的数字pass，
毕竟没有数字是0开头的嘛。
处理完这两种特殊情况，我们来考虑下一般情况。既然是回文数，
那肯定可以翻转嘛，不能翻转的肯定不是回文数。
在上一题中我们介绍了数学的反转方法，这里正好用到。

public boolean isPalindrome(int x) {
        if(x<0 || (x%10==0 && x!=0))
            return false;        
        int res = 0;
        int y = x;
        while(x!=0){
            res = res*10+x%10;
            x = x/10;
        }
        return res==y;
    }

 

有了上一题的经验，我们快速的写出了翻转的方法。你可能会问，上一题中我们思考了
溢出的情况，那么这题呢?能想到这一点说明你和我一样严谨（手动滑稽）。
事实上我们这里并不需要担心溢出的问题，因为众所周知，int只有4字节32位字符，
溢出的话并不代表int无法表示，只是会做截取，而这个截取的值肯定与原值不同，
就如下图一样。

题目13. 罗马数字转整数

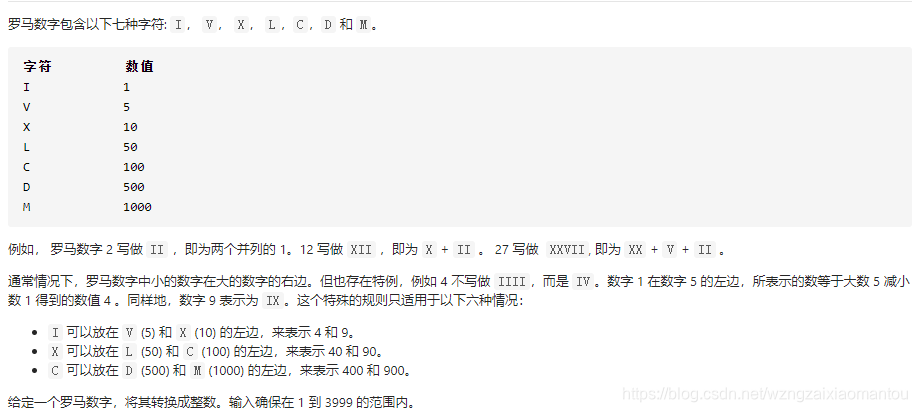
第一反应是找规律
IV = 5 -1 = （-1）1 +5 = 4
VI = 5 + 1 = 5 + 11 = 6
XL = 50 - 10 = (-1)*10 + 50 = 40
LX = 50 + 10 = 50 + (1)*10 = 60

我们发现，如果左边的值比右边的小，则做减法，否则就是加法。
于是我们可以for循环做一次遍历，从第二个元素开始，每一个都跟
前一个元素比较大小，判断加减。有个细节需注意，我们是在第二个节点
时才判断对第一个节点的加减，因此当跳出循环时，末尾元素没有加进去,
由于最后一位元素没有右边一位，因此最后一位元素必定做加法。

public int romanToInt(String s) {
        int sum = 0;
        char[] c = s.toCharArray();
        int previous = judgeSize(c[0]);
        for(int i = 1;i < c.length; i ++) {
            int next = judgeSize(c[i]);
            if(previous < next) {
                sum = sum -previous;
            } else {
                sum = sum + previous;
            }
            previous = next;
        }
        sum = sum + previous;
        return sum;
    }
    
    private int judgeSize(char ch) {
        switch(ch) {
            case 'I': 
                return 1;
            case 'V': 
                return 5;
            case 'X': 
                return 10;
            case 'L': 
                return 50;
            case 'C': 
                return 100;
            case 'D': 
                return 500;
            case 'M': 
                return 1000;
            default: 
                return 0;
        }
    }

 

这里的switch也可以用HashMap实现映射关系的存储，但是效率上
可能存在一定消，毕竟建哈希表的时间也不是天上掉下来的嘛。
时间复杂度为O(n)（n为罗马数字的长度）

题目14. 最长公共前缀

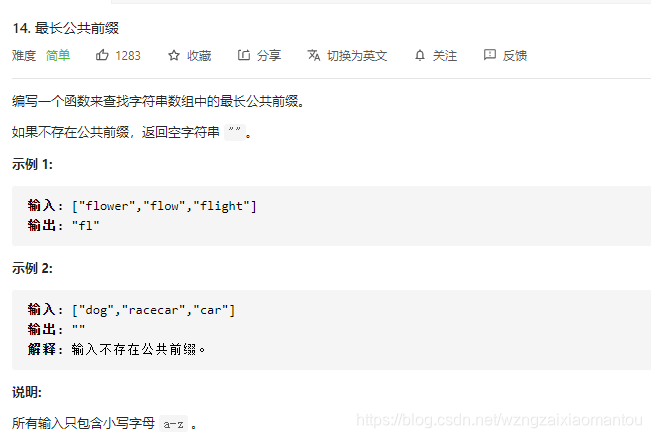
还是从例子中找思路
flower，flow，flight
可以得出最长公共前缀为fl
不过我们可以看出，如果只有前两个元素，则结果是flow
在看下面的例子
flower，flow，flight，fow
则最长公共前缀变成了f
以此类推，第一个元素和第二个元素的最长公共前缀，一定包含
或等于（前提是公共前缀存在）第二个元素和第三个元素的前缀
因此，我们可以先把第一个元素给取出来，作为最长公共前缀（即自身与自身匹配）
然后在与第二个元素逐字符匹配，可以获取这两个元素的最长公共前缀，
再将结果与第三个元素逐个匹配，可以获得前三个元素的最长公共前缀
以此类推,直至结尾（或结果为空们则直接返回）就可以得出最终结果

    public String longestCommonPrefix(String[] strs) {
        if (strs.length == 0)
            return "";
        String res = strs[0];
        for (int i = 1; i < strs.length; i++) {
            int j = 0;
            for (; j < res.length() && j < strs[i].length(); j++) {
                if (!(res.charAt(j) == strs[i].charAt(j))) {
                    break;
                }
            }
            res = res.substring(0, j);
            if ("".equals(res))
                return res;
        }
        return res;
    }

 

时间复杂度为O(mn)（n为数组长度，m为数组中每个字符串平均长度）

题目20. 有效的括号

左右括号的对应关系第一反应是联想到了key-value的关系映射。
利用栈的先进后出功能完美解决。
首先，奇数长度字符串先肯定不符合，pass。再来一般情况，
每次遇到左括号就压入，遇到右括号就取出栈顶元素判断是否是
与此右括号对应的左括号（此对应关系利用hashmap实现），如不对应
则说明不符合，pass。最后，因为左右对应，最后的栈应该是空的，
如果遍历完一次之后栈不空，则说明有括号未匹配上，pass。

    public boolean isValid(String s) {
        if (s.length() % 2 == 1) {
            return false;
        }
        HashMap<Character, Character> brackets = new HashMap<Character, Character>();  
        brackets.put(')','(');
        brackets.put('}','{');
        brackets.put(']','[');
        Deque<Character> stack = new LinkedList<Character>();
        for (int i = 0; i < s.length(); i++) {
            char ch = s.charAt(i);
            if (brackets.containsKey(ch)) {
                if (stack.isEmpty() || stack.peek() != brackets.get(ch)) {
                    return false;
                }
                stack.pop();
            } else {
                stack.push(ch);
            }
        }
        return stack.isEmpty();
    }

 

复杂度为O(n^2)（deque内部的getNode也是用了while实现，因此为n*n）