2021.09.15膜你赛
膜你赛
2021.09.15膜你赛
T1
Description
正的魔法师利用的都是万物众生自然之力。
魔法师正在绘制用于大魔法的魔法聚灵阵，此聚灵阵一共有n个魔力源点，魔力源点与魔力源点之间由一条魔力链相连，每条魔力链上都有一定数量的魔力石，每两个魔力源点之间有且只有一条路径——没错，就是一棵魔法树！
魔法阵中的两两不同节点会相互呼应，来达到魔力增幅的效果，任意两个点的共振魔力定义为这两个点的路径上每条魔力链上的魔力石的最大值，魔法阵的总增幅效果为魔法阵中所有点对的共振魔力的和。
Solution
最暴力的做法就是用树剖维护最大值，\(n^2\) 枚举点对。但是只有 50 分，暴力浪费时间，直接想正解。
发现这道题跟以前做的一道题很像，那道题好像是要求经过一条边的黑白点对数，做法是求出左边的黑/白点的数量，右边的白/黑点的数量，乘法原理相乘，于是往这方面想。
发现一条边能做贡献，肯定是它是这条链上的最大边。
比如说下面这个图，最大边所能做出的贡献就是 \(1\times5 \times 9\)
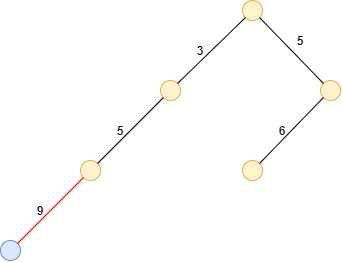
而对于次大边，它的贡献为 \(4\times 1\times 6\)
再来一条，贡献为 \(1\times 3 \times 5\)
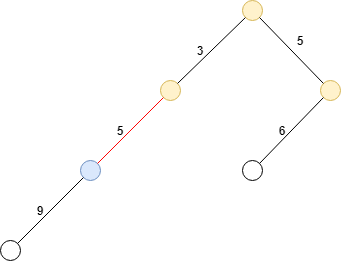
对于与当前边相等的边，其加过的贡献不再计算。
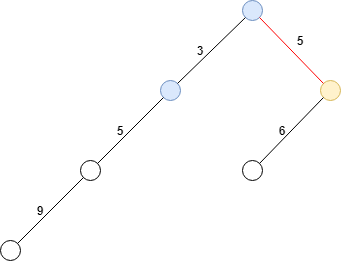
回顾我们计算贡献的过程，发现，我们计算过的边就像被删掉了一样，其左边或右边的边不再被贡献，我们不妨把它们删掉，这样左右边点的个数就是我们需要的点的个数。
但是删除操作似乎有点困难，BS：LCT啊 ，我们考虑加边。然后并查集查询。（莫名耳熟
将边从大到小排序，加入并查集中，因为最小的边贡献也是最少的。
最后，关于怎么维护左右边的大小。
如果存在多个连通块，
比如说这条边，我们将个数少的的加入个数多的，那么左边的 siz 就会加上右边的 siz,我们将 siz 记录到根节点上，我们用这个合并块的 siz 减去原来块的 siz 就是左边的个数。说可能说病清楚，看代码吧。另外，我的思路代码跟BS的一毛一样，就是犯了个 SB 错误，并查集写成 return f[x] 了，\(100pts\to 0pts\)
Code
/*
* @Author: smyslenny
* @Date: 2021.09.
* @Title:
* @Main idea:
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iomanip>
#include <cstring>
#include <cstdlib>
#include <queue>
#include <vector>
#define int long long
#define INF 0x3f3f3f3f
#define orz cout<<"LKP AK IOI\n"
#define MAX(a,b) (a)>(b)?(a):(b)
#define MIN(a,b) (a)>(b)?(a):(b)
using namespace std;
const int mod=999999937;
const int M=5e5+5;
int n;
int read()
{
int x=0,y=1;
char c=getchar();
while(c<'0' || c>'9') {if(c=='-') y=0;c=getchar();}
while(c>='0' && c<='9') { x=x*10+(c^48);c=getchar();}
return y?x:-x;
}
struct ed{
int u,v,w;
}edge[M<<1];
int Ans,du[M],js,siz[M],f[M];
int find(int x)
{
if(f[x]==x) return x;
return f[x]=find(f[x]);
}
bool cmp(ed a,ed b)
{
return a.w<b.w;
}
signed main()
{
// freopen("magic.in","r",stdin);
// freopen("magic.out","w",stdout);
n=read();
for(int i=1,u,v,w;i<n;i++)
edge[i].u=read(),edge[i].v=read(),edge[i].w=read();
sort(edge+1,edge+n,cmp);
for(int i=1;i<=n;i++) f[i]=i,siz[i]=1;
for(int i=1;i<n;i++)
{
int u=edge[i].u,v=edge[i].v;
int fa=find(u),fb=find(v);
if(fa!=fb)
{
f[fb]=fa;
siz[fa]+=siz[fb];
}
Ans=(Ans+siz[fb]*(siz[fa]-siz[fb]+mod)%mod*edge[i].w%mod)%mod;
}
printf("%lld\n",Ans%mod);
return 0;
}
/*
7
1 2 2
1 3 3
2 4 2
2 5 4
3 6 1
3 7 3
*/
T2
Descrpiton
小皮同学在打一个游戏，尝试第一关 BOSS 2147483647 次后放弃了，他从网上找到了秘籍，他发现这个游戏居然有 \(m\) 个彩蛋！每个彩蛋都是形如以下格式：
只要满足一定的条件（小皮发现触发这些条件都不难）并打倒第 \(i\) 关的BOSS，你将自动跳转到第 \(j\) 关的 BOSS 前（\(j\) 可能小于 \(i\)），并且第 \(j\) 关的 BOSS 会变得很简单，简单到小皮这样的手残都能轻松解决
“卧槽，怪不得这游戏这么难，原来还有这种操作！”
可是……小皮连……第一关都过不了啊……而那本秘籍居然连这个都有解决方案！小皮可以在游戏一开始的时候疯狂地卡BUG，然后他会被传送到一个由他指定的关卡并且攻击力防御力全部变成 \(999999999\)，他就能轻松打到BOSS，可是由于打倒 BOSS 后播放剧情动画会使这个 BUG 被修复，在下一关就不能用了。
而小皮的策略就是先利用卡 BUG 的方式跳到某一关，然后一直尽可能保持着触发彩蛋 -> 打BOSS的过程(同一关可能由多种不同彩蛋，小皮可以选择其中一个触发)，知道到达了一个关卡没有彩蛋可用。
小皮想知道他从每一关作为起点出发，能利用彩蛋到达的编号最大的关卡分别是多少？（包含起点本身）
Solution
做过好几遍了，建反边搜索就可以了,从没有搜到的点中找最大点，他能到达的点的答案就是这个点。然后遍历一遍就行了。
/*
* @Author: smyslenny
* @Date: 2021.09.
* @Title:
* @Main idea:
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iomanip>
#include <cstring>
#include <cstdlib>
#include <queue>
#include <vector>
#define ll long long
#define INF 0x3f3f3f3f
#define orz cout<<"LKP AK IOI\n"
#define MAX(a,b) (a)>(b)?(a):(b)
#define MIN(a,b) (a)>(b)?(a):(b)
using namespace std;
const int mod=998244353;
const int M=1e5+5;
int n,m,dis[M];
int read()
{
int x=0,y=1;
char c=getchar();
while(c<'0' || c>'9') {if(c=='-') y=0;c=getchar();}
while(c>='0' && c<='9') { x=x*10+(c^48);c=getchar();}
return y?x:-x;
}
struct cd{
int fr,to;
}q[M];
struct ed{
int u,v,net;
}edge[M<<1];
int head[M],num;
void addedge(int u,int v)
{
edge[++num].u=u;
edge[num].v=v;
edge[num].net=head[u];
head[u]=num;
}
namespace substack1{
int Max;
int find(int x,int fa)
{
for(int i=head[x];i;i=edge[i].net)
{
int v=edge[i].v;
if(v==fa) continue;
Max=max(Max,v);
find(v,x);
}
}
void main()
{
for(int i=1;i<=m;i++)
{
q[i].fr=read(),q[i].to=read();
addedge(q[i].fr,q[i].to);
}
for(int i=n;i>=1;i--)
{
Max=i;
find(i,i);
printf("%d ",Max);
}
}
}
namespace substack2{
int Ans[M];
void dfs(int u,int x)
{
if(Ans[u]) return;
Ans[u]=x;
for(int i=head[u];i;i=edge[i].net)
dfs(edge[i].v,x);
}
void main()
{
for(int i=1;i<=m;i++)
{
q[i].fr=read(),q[i].to=read();
addedge(q[i].to,q[i].fr);
}
for(int i=n;i>=1;i--)
dfs(i,i);
for(int i=1;i<=n;i++)
printf("%d ",Ans[i]);
}
}
int main()
{
// freopen("contra.in","r",stdin);
// freopen("contra.out","w",stdout);
n=read(),m=read();
substack2::main();
return 0;
}
/*
5 3
1 2
2 4
3 5
*/
T3
Descrption
铲铲同学来到了世界上最繁华的国家——金钱国，在金钱国中，无论做什么事情都要金钱。
在金钱国一共由 \(n\) 个城市（编号为为 \(0 \sim n-1\)），城市和城市之间通过城际告诉公路相连，一共有m条双向城际高速公路，而经过每一条城际高速公路都要收各自的费用，现在铲铲同学通过飞机降落在了金钱国的 \(S\) 号城市，但铲铲最终的目标是会见金钱国在 \(T\) 市的一个客户。
现在问题来了——铲铲最小要花费多少的过路费？
嗯——最短路裸题。
啊不对出题人忘记说了，铲铲有 \(k\) 张贵宾卡，每张贵宾卡都可以让铲铲在经过任意一条路的时候不交过路费，贵宾卡是消耗形的，用一张少一张。
Solution
分层图最短路板子题，我没看出来！写了暴力50分跑了
Code
/*
* @Author: smyslenny
* @Date: 2021.09.
* @Title:
* @Main idea:
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iomanip>
#include <cstring>
#include <cstdlib>
#include <queue>
#include <vector>
#define ll long long
#define INF 0x3f3f3f3f
#define orz cout<<"LKP AK IOI\n"
#define MAX(a,b) (a)>(b)?(a):(b)
#define MIN(a,b) (a)>(b)?(a):(b)
using namespace std;
const int mod=998244353;
const int M=1e5+5;
int n,m,k,s,t;
int read()
{
int x=0,y=1;
char c=getchar();
while(c<'0' || c>'9') {if(c=='-') y=0;c=getchar();}
while(c>='0' && c<='9') { x=x*10+(c^48);c=getchar();}
return y?x:-x;
}
struct ed{
int u,v,w,net;
}edge[M<<1];
struct edg{
int u,v,w;
}Ed[M*20];
int head[M],num;
void addedge(int u,int v,int w)
{
edge[++num].u=u;
edge[num].v=v;
edge[num].w=w;
edge[num].net=head[u];
head[u]=num;
}
int dis[M],vis[M];
struct node{
int w,u;
bool operator < (const node &x)const
{
return w>x.w;
}
};
priority_queue<node> q;
void dij(int s)
{
dis[s]=0;
q.push(node{0,s});
while (!q.empty())
{
node t=q.top();
q.pop();
int u=t.u;
if(vis[u]) continue;
vis[u]=1;
for(int i=head[u];i;i=edge[i].net)
{
int v=edge[i].v;
if(dis[v]>dis[u]+edge[i].w)
{
dis[v]=dis[u]+edge[i].w;
q.push(node{dis[v],v});
}
}
}
}
namespace substack1{
void main()
{
memset(dis,63,sizeof(dis));
dij(s);
printf("%d\n",dis[t]);
}
}
namespace substack2{
int Min=INF;
void main()
{
for(int i=1;i<=m;i++)
{
memset(dis,63,sizeof(dis));
memset(vis,0,sizeof(vis));
int x=edge[i].w;
edge[i].w=0;
dij(s);
Min=min(Min,dis[t]);
edge[i].w=x;
}
printf("%d\n",Min);
}
}
namespace substack3{
priority_queue<node> q;
int Ans;
void Dij(int s)
{
dis[s]=0;
q.push(node{0,s});
while(!q.empty())
{
node t=q.top();
q.pop();
int u=t.u;
if(vis[u]) continue;
vis[u]=1;
for(int i=head[u];i;i=edge[i].net)
{
int v=edge[i].v;
if(dis[v]>dis[u]+edge[i].w)
{
dis[v]=dis[u]+edge[i].w;
q.push(node{dis[v],v});
}
}
}
}
void main()
{
for(int i=0;i<m;i++)
for(int j=0;j<=k;j++)
{
addedge(Ed[i].u+j*n,Ed[i].v+j*n,Ed[i].w);
addedge(Ed[i].v+j*n,Ed[i].u+j*n,Ed[i].w);
if(i!=k)
{
addedge(Ed[i].u+j*n,Ed[i].v+(j+1)*n,0);
addedge(Ed[i].v+j*n,Ed[i].u+(j+1)*n,0);
}
}
memset(dis,63,sizeof(dis));
memset(vis,0,sizeof(vis));
Ans=INF;
Dij(s);
for(int i=0;i<=k;i++)
Ans=min(Ans,dis[t+i*n]);
printf("%d\n",Ans);
}
}
int main()
{
// freopen("pass.in","r",stdin);
// freopen("pass.out","w",stdout);
n=read(),m=read(),k=read();
s=read(),t=read();
for(int i=0,u,v,w;i<m;i++)
{
u=read(),v=read(),w=read();
Ed[i].u=u,Ed[i].v=v,Ed[i].w=w;
}
// if(k==0) substack1::main();
// else if(k==1) substack2::main();
// else
substack3::main();
return 0;
}
/*
5 5 1
0 3
3 4 5
0 1 1
0 2 8
1 2 6
2 4 3
*/
