LCT学习笔记

LCT学习笔记

前言

老吕又讲了LCT，据他说特别简单，于是就强行灌输（雾。
打字两分钟，画图两小时。。。

引入

• 维护一棵树，维护以下的操作：

  • 链上求和
  • 链上求最值
  • 链上修改
  • 子树修改
  • 子树求和

可能你第一眼想的是树链剖分，的确，这都是树链剖分的基本操作。

但是如果再增加一些操作呢

• • 换根
  • 断开树上的一条边
  • 连接两个点，保证连接后仍是一棵树

线段树就不好做了，于是我们的 LCT 就出场了。

注：树剖也是可以换根的，可能我上面说的不清楚，具体怎么换可以参考这篇博客。我只是说不太好做。（可能我太菜了）。

简介

LCT，全称 Link-Cut Tree，一种动态树，用来解决动态的树上问题。说它是树也不大准确，它维护的其实是一个森林。据我不可信的猜测，这个名字可能是由于这个数据结构特有的特色来命名的，也就是 Link，Cut，支持树上的删边，加边。这一点是普通线段树没法做到的，LCT的 access 也是他的一大特色，也是常用的一个函数。（个人感觉）

构造

我们在学习树链剖分的时候，就知道，将链进行剖分，主要有三种形式：

1.重链剖分。
只要是按照子树大小进行剖分，就是把儿子数最多的儿子当做重儿子，重儿子连成的链叫做重链。

2.长链剖分。
并不是很常见，我也不到了解。

3.实链剖分。
将树上的链分成虚实两种，一个点最多只有一个孩子作为实孩子。连接实孩子的称为实边，实边组成的链称为实链。

我们在 LCT 中就是采用的是实链剖分，其中，实孩子是不固定的，它可以通过我们的修改而发生改变，我想，这也是 LCT 的一个动态，当然，其主要的动态还是动态删边和加边。因此，我们需要选用更灵活的数据结构。

维护一条链，理论上 FHQ-Treap 和 Splay 都是可以的，但是 FHQ-Treap 要比 Splay 多一个 \(\log\) ，而且网络上的题解大部分都写的是 Splay，因此，这里推荐 Splay 的写法，不会 Splay 的可以去学习一下，因为这是非常重要的一部分。因为我也没写过FHQ-Teap的。

我们在之前说过，一个点顶多只有一个实孩子，也就是说一条实链上，每个节点的深度在原树中都是不同的，因此，我们把深度作为关键字用 Splay 维护，对于一个节点，它的左儿子的深度要比它小，右儿子的深度要比它大。

这里补充一下两个概念：

原树：也就是我们对其进行剖分的树。在我们实现的时候，原树是 不存储 的，只是为了方便我们理解。

辅助树：也就是一棵splay，或者说一些 Splay。

• 它维护的是原树中的一条实链，在程序中真正操作的都是辅助树。中序遍历这些点的时候，其对应的就是原树中的一条链。

• 在 LCT 中每棵 Splay 的根节点的指向 原树 中 这条链 的链顶的父亲节点（即链最顶端的点的父亲节点）。主要的特点在于儿子认父亲，而父亲不认儿子，对应原树的一条 虚边。

基础操作

我们先造一颗树。这是一棵原树。

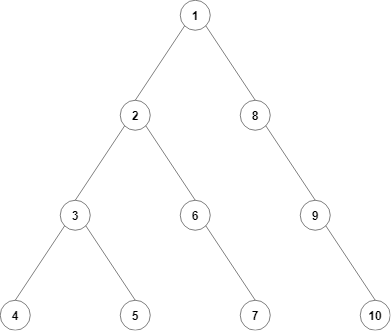
我们选择一些边作为虚边，选择一些边作为实边。

然后，让我们画出辅助树。

我们找出其中的 Splay，大概就是这个亚子。

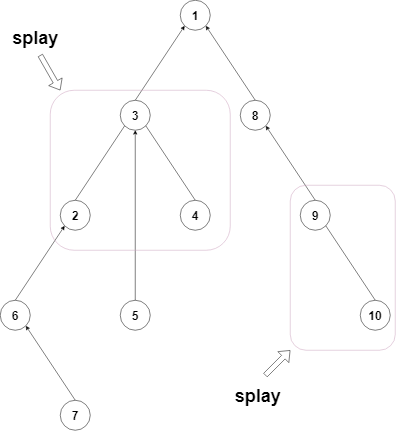
了解完这些之后，我们开始今天的重点。

变量声明

我习惯将变量放到结构体里。

• tree.ch[0/1] 左右儿子

• f[N] 父亲

• tree.sum 路径权值和

• tree.val 点权

• tree.laz[N] 翻转标记

主要的函数：

• link(x,y)连接两个点

• cut(x,y)：断开两个点间的边

• access(x)：把 \(x\) 点下面的实边断开，并把 \(x\) 点一路向上边到树的根

• makeroot(x)：把 \(x\) 点变为树的根

• find(x)：查找 \(x\) 所在树的根

• isroot(x)：判断 \(x\) 是否是辅助树的根

• split(x,y) : 提取出 \(x,y\) 间的路径

• update(x,y) ： 修改 \(x\) 的点权为 \(y\)。

  当然还有 rotate ， splay，pushup，pushdown ，不过这些都是线段树或 Splay 的基本操作，就不详细展开了。

accsee

作用：断开当前点连的实链，到根节点连一条实链。

方法：把 \(x\) 点伸展到splay的根，再把它的右子树连到 \(t\) ， \(t\) 的初值为 0，也就了与下一层的实链断开了，然后 \(t\) 更新为 \(x\)，而 \(x\) 更新为 \(x\) 的父亲，继续向上连接。因为我们现在的连接，父亲认儿子，儿子认父亲，一直到根，也就到根连接了一条实链。

假设我们 \(access(9)\) ，我们的图就变成了这样。原谅我不会制作动图，没有详细的变化过程。

void access(int p) 
{
	int t=0;//因为当前点是这条链的最后一个点，旋转到根之后右边的点就是当前点之后的点，也就是要断开的点
	while(p)
	{
		splay(p);//把 p 伸展到根节点， 
		rson(p)=t;//不断让父亲向它连边，也就是连上了实边 
		t=p;
		p=f[p];
		push_up(p);
	}
}

makeroot

作用：把x点变为所在原树的根。

方法：首先的把 \(x\) 点 \(access\) 到根，把 \(x\) 点到根就变成了一个 Splay，然后把 \(x\) 伸展到根。由于 \(x\) 点是辅助树在原树中最下面的点，所以这时其它的点都在 \(x\) 的左子树上，只要把左子树变成右子树，\(x\) 也就变成了根。

我们上面 \(accsee(9)\) ，不妨就继续让 \(9\) 变成根。先 Splay 一下。

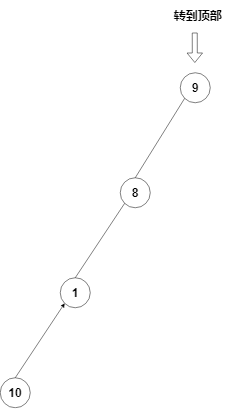
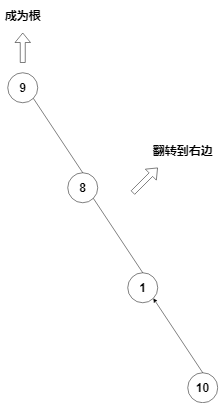
void makeroot(int p)//是当前点变成原树里的根节点 
{
	access(p);//到根节点连实链，也就是一颗 splay
	splay(p);//将当前点转到根节点
	tree[p].laz^=1//由于 x 点是最后一个，当前为根节点时所有的点都在他的左边，^一下让所有的点都在他右边，就变成了根了
}

findtoot

作用：查找原树的根

我们想一下，在辅助树中，怎么才能找到原树的根呢？

我们发现，位于最顶部的 Splay，它的最左边的孩子为原树的根，因为我们要保证 Splay 的形态，先要保证它的中序遍历和原树一致。

方法：首先把 \(x\) 点 \(access\) 到原树的根，并把它 Splay 到辅助树的根，这时原树的根就是 \(x\) 左子树中最左侧的点。

再借用上面的 \(access(9)\) 和 \(Spaly(9)\)

int find(int x)//找原树的根 
{
	access(x);//x到根建一颗splay
	splay(x);//将 x 伸展到根节点
	while(lson(x)) push_down(x),x=lson(x);//因为原树根节点肯定就是中序遍历的第一个点，也就是最顶上的
	return x;// splay的最左边的儿子，一直找左儿子就行了 
}

split

作用：提取出 \(x,y\) 间的路径

我们再 \(makeroot(9)\) ，图在前面，就不放了，我们 \(access(10)\) 再 \(Splay(10)\) 。

void split(int x, int y) {
    makeroot(x);//首先把x置为根节点 
    access(y);//生成一颗 Splay
    splay(y);
    //y维护的就是x - y 路径上的信息 
}

link

作用：把 \(x\) 点和 \(y\) 点之间连一条边
方法：把 \(x\) 点变成所在原树的根，然后把 \(x\) 点的父亲变成 \(y\) 就可以了。

比如说加一条连向 \(9\) 的边。

void link(int x,int y)//连边
{
	makeroot(x);//使p变成根节点
	f[x]=y;//x变成y的父亲，也就是连了边
}

cut

作用：把 \(x\) 点和 \(y\) 点之间的边删掉
方法：把 \(x\) 点变成所在原树的根，然后把 \(y\) 点 \(access\) 到根，Splay \(y\) 到辅助树的根，然后断开y与它左孩子间的边。由于 \(x\) 是原树的根，\(y\) 是树中的一点，所以就 \(y\) 点通过 \(access\) 和 \(x\) 点连到一个辅助树中时，\(x\) 点一定是它们所在实链的链顶。而 \(y\) splay到辅助树的根时，如果 \(x\),\(y\) 间有一条边，则 \(x\)一定是 \(y\) 的左孩子。

比如说删去 \(8\to 9\) 这条边。

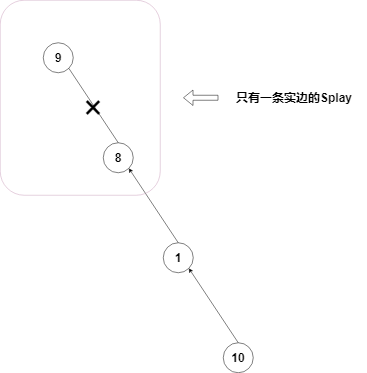
void cut(int x,int y)//删边
{
	makeroot(x);//x变成根节点
	access(y);//y通向 x 减了一个实链，也就是一颗 splay，因为 x,y之间有边，所以这颗splay 里面只有两个点
	splay(y);//将 y 转到顶部 
	if(lson(y)!=x ||rson(x)) return;//两者之间本来就没有边
	f[x]=0;//删去原来连边的信息 
	lson(y)=0;
	push_up(x);
}

isroot

作用：判断是否是splay的根
方法：splay的根结点的父亲并不认这个孩子。
注意:原树的根的父亲点是 \(0\)

bool isroot(int x)//判断当前点是否是实链的根节点
{//当前点是根节点因为这它认父亲，父亲不认儿子 
	return lson(f[x])!=x && rson(f[x])!=x; 
}

下面的部分都是基础操作，Splay 有个地方有点不一样，可以看见。

pushup

void push_up(int p)
{
	tree[p].sum=tree[lson(p)].sum^tree[rson(p)].sum^a[p];
    or
    tree[p].sum=tree[lson(p)].sum+tree[rson(p)].sum+a[p];
}

pushdown

void ff(int p) 
{
	swap(lson(p),rson(p));
	tree[p].laz^=1;
}
void push_down(int p)
{
	if(!tree[p].laz) return;
	if(lson(p)) ff(lson(p));
	if(rson(p)) ff(rson(p));
	tree[p].laz=0;
}

rotate

void rotate(int x,int op)
{
	int y=f[x];
	if(!isroot(y))
		tree[f[y]].ch[rson(f[y])==y]=x;//原先父亲节点与其父亲节点的边断开，连上现在的这个点 
	f[x]=f[y];//儿子节点的爸爸换成爷爷 
	if(tree[x].ch[op])//儿子节点op儿子有的话，改变他的父亲为父亲 
		f[tree[x].ch[op]]=y;
	tree[y].ch[!op]=tree[x].ch[op];//父亲的儿子变成儿子的儿子 
	f[y]=x;//父亲的父亲变成儿子 
	tree[x].ch[op]=y;//儿子的对应儿子变成父亲
	push_up(y); 
	//注：注释里的父亲，儿子，爷爷，都表示没变化之前的称谓 
}

spaly

这里讲一下和普通 Splay 的一点区别，就是我们先用栈将我们接下来要旋转的点存储下来，然后一起 pushdown 。这样就不用边旋转边 pushdown。

int sta[M],top;//为了将懒惰标记一气儿下传 
void splay(int x)
{
	sta[++top]=x;
	for(int i=x;!isroot(i);i=f[i]) sta[++top]=f[i];
	while(top) push_down(sta[top--]);//splay之前先将要旋转的链上的懒惰标记全部下穿，免去了边旋转边下传的麻烦
	while(!isroot(x))//当前点不是根 
	{
		if(!isroot(f[x]))//父亲也不是根 
		{	
			if((rson(f[x])==x)^(rson(f[f[x]])==f[x]))//不在一边 
				rotate(x,lson(f[x])==x);//旋转当前节点 
			else
				rotate(f[x],lson(f[f[x]])==f[x]);//链的情况，旋转父亲节点才能改变形态，旋转父亲节点 
		}
		rotate(x,lson(f[x])==x);
	}
	push_up(x);
}

习题

• luogu P3690 【模板】动态树（Link Cut Tree)

  代码

• luogu P2147 [SDOI2008] 洞穴勘测

  代码

• luogu P2590 [ZJOI2008]树的统计

  不知道哪里错了，但是可以参考的代码，或许帮我调调？

• bzoj2158

• bzoj2002

• BZOJ2631tree(LCT模板题，路径加，路径乘，求路径点权和)

• BZOJ2002[Hnoi2002]弹飞绵羊(LCT练习题，重点在于如何转化成LCT)

• BZOJ3669[Noi2014]魔法森林(LCT经典题，利用LCT解决二维最小生成树)

• BZOJ4530[Bjoi2014]大融合(LCT维护子树信息)

• BZOJ3091城市旅行(LCT区间信息合并)

后面的没做，做了有时间再补代码。

参考资料

oi_wiki

flashhu大佬的博客

亲学长的博客

老师的课件