拉格朗日插值学习笔记
拉格朗日插值学习笔记
简介
在数值分析中,拉格朗日插值法是以法国十八世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法。许多实际问题中都用函数来表示某种内在联系或规律,而不少函数都只能通过实验和观测来了解。如对实践中的某个物理量进行观测,在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。这样的多项式称为拉格朗日(插值)多项式。数学上来说,拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。拉格朗日插值法最早被英国数学家爱德华·华林于1779年发现,不久后(1783年)由莱昂哈德·欧拉再次发现。1795年,拉格朗日在其著作《师范学校数学基础教程》中发表了这个插值方法,从此他的名字就和这个方法联系在一起。

插值
对于学习拉格朗日插值之前,我们首先要弄懂,什么叫插值?
插值 数学领域数值分析中的通过已知的离散数据求未知数据的过程或方法。
概念可能不好理解,举个栗子:
我们给出:
\(x_0=1,y_0=3\)
\(x_1=2,y_0=5\)
\(x_2=4,y_0=8\)
\(x_3=5,y_0=4\)
求当 \(x=3\) 时,\(y\) 的值。
首先,我们可以通过列方程的办法,求出函数,将 \(x\) 带入求解。
如,我们设 \(y=ax^3+bx^2+cx+d\)
\(\begin{cases} a+b+c+d=3 \\8a+4b+2c+d=5 \\ 64a+16b+4c+d=8 \\125a+25b+5c+d=4 \end{cases}\)
然后联立求解,这里就不给出求解过程了,需要用到高斯消元。
这样做的复杂度是 \(O(n^3)\) 的,有点慢,我们考虑用拉格朗日差值优化这一问题。
拉格朗日插值
我们首先考虑 \(x_0\) ,建立一个函数,使其经过 \((x_0,1),(x_1,0),(x_2,0),(x_3,0)\)。
为什么这么构造,为什么不构造一个经过 \((x_0,2),(x_1,1),(x_2,1),(x_3,1)\) 的函数或者其他的呢,这个我们一会再说。
我们先考虑一下,如何才能构造这样一个函数呢?
设
\(y=\frac{(X-x_1)\times(X-x_2)\times(X-x_3)}{(x_0-x_1)\times(x_0-x_2)\times(x_0-x_3)}\)
我们不难发现,当 \(X=x_0\) 时,分子变成了 \((x_0-x_1)\times(x_0-x_2)\times(x_0-x_3)\),这与分母相同,于是式子可化为 \(1\)。再看,当 \(X=x_1,X=x_2,X=x_3\) 时,分子会变为 \(0\),于是,我们完成了构造的一大半。
我们发现,当前的函数只是经过了 \((x_0,1)\),我们想要的是它经过 \((x_0,y_0)\),怎么办呢。
很简单,我们直接在原始的基础上乘上一个 \(y_0\)。
\(y=\frac{(X-x_1)\times(X-x_2)\times(X-x_3)}{(x_0-x_1)\times(x_0-x_2)\times(x_0-x_3)}\times y_0\)
此时,由于当 \(X=x_1,X=x_2,X=x_3\) 时,函数值为 \(0\),我们乘上一个 \(y_0\) 不会对其有影响,于是,我们就构造出一个经过 \((x_0,y_0)\) 的函数。
如图:

此时,我们再回答之前的问题:为什么要使函数经过 \((x_0,1),(x_1,0),(x_2,0),(x_3,0)\)?
按照我自己的理解,这其实是为了之后乘 \(y_0\) 做铺垫,因为这样我们的 \(x_0\) 就对应了 \(y_0\) ,而其他值依旧为 \(0\) ,满足了我们的构造要求:只经过 \((x_0,y_0)\) 。而如果是构造一个经过 \((x_0,2),(x_1,1),(x_2,1),(x_3,1)\) 的函数,还是应该有办法让它经过 \(y_0\) 的,我没有尝试过,但是应该会非常麻烦,所以我觉得这个构造的方式也是拉格朗日插值的一个精妙之处。
返回题目,这样做还是不够的,我们的目的是为了构造经过这四个点的函数,这才经过了一个呢。
我们根据上面的方法,依次构造出只经过 \((x_1,y_1)\) 的函数,只经过 \((x_2,y_2)\) 的函数,只经过 \((x_3,y_3)\) 的函数,
\(y0=\frac{(X-x_1)\times(X-x_2)\times(X-x_3)}{(x_0-x_1)\times(x_0-x_2)\times(x_0-x_3)}\times y_0\)
\(y1=\frac{(X-x_0)\times(X-x_2)\times(X-x_3)}{(x_1-x_0)\times(x_1-x_2)\times(x_1-x_3)}\times y_1\)
\(y2=\frac{(X-x_0)\times(X-x_1)\times(X-x_3)}{(x_2-x_0)\times(x_2-x_1)\times(x_2-x_3)}\times y_2\)
\(y3=\frac{(X-x_0)\times(X-x_1)\times(X-x_2)}{(x_3-x_0)\times(x_3-x_1)\times(x_3-x_2)}\times y_3\)
然后,我们把它们加起来。
\(f(x)=y0+y1+y2+y3\)
图像如下:
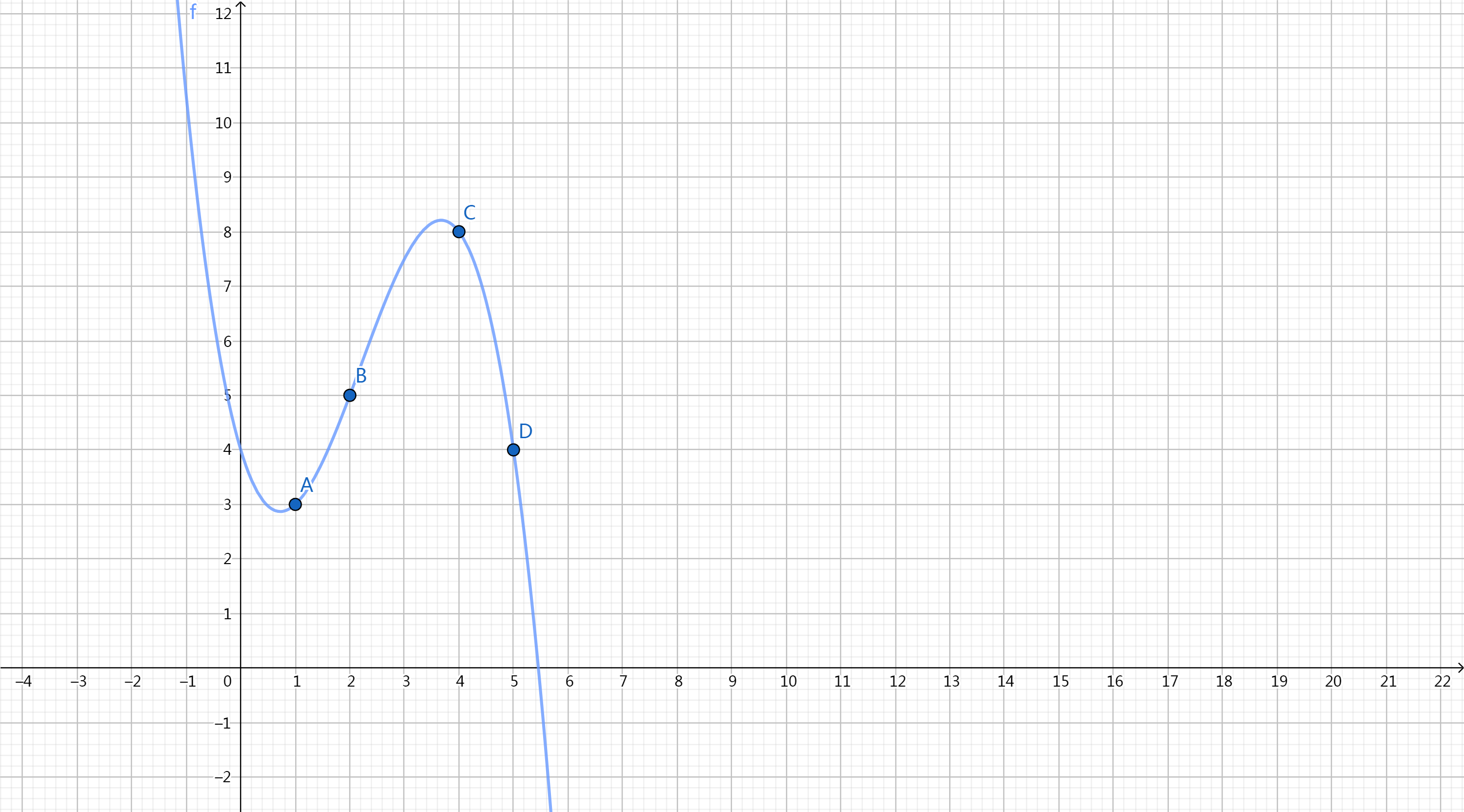
由于这四个函数都只经过了各不相同的四个点,其余点的值都为 \(0\),因此,这个解析式就满足了我们的要求,我们此时只要将待求的 \(x\) 带入式子,就可以求出对应的值。
如我们的栗子:
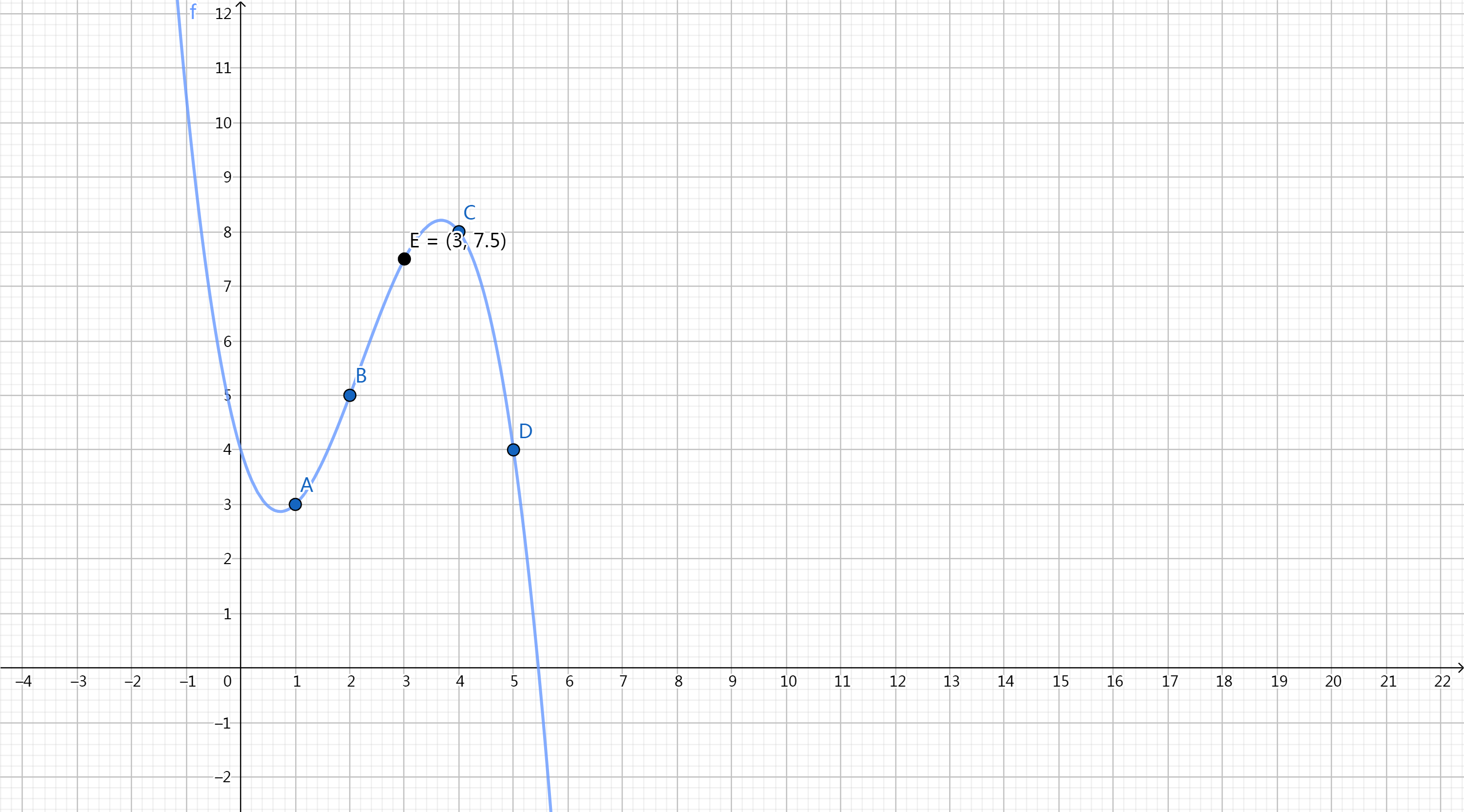
我们再回头看我们的函数
\(f(x)=y0+y1+y2+y3\)
\(=\frac{(X-x_1)\times(X-x_2)\times(X-x_3)}{(x_0-x_1)\times(x_0-x_2)\times(x_0-x_3)}\times y_0+\frac{(X-x_0)\times(X-x_2)\times(X-x_3)}{(x_1-x_0)\times(x_1-x_2)\times(x_1-x_3)}\times y_1+\frac{(X-x_0)\times(X-x_1)\times(X-x_3)}{(x_2-x_0)\times(x_2-x_1)\times(x_2-x_3)}\times y_2+\frac{(X-x_0)\times(X-x_1)\times(X-x_2)}{(x_3-x_0)\times(x_3-x_1)\times(x_3-x_2)}\times y_3\)
\(=y_0\times\prod\limits_{j=1}^{3}\frac{x-x_j}{x_0-x_j}+y_1\times \prod\limits_{j=0,j\not=1}^{3}\frac{x-x_j}{x_1-x_j}+y_2\times\prod\limits_{j=0,j\not=2}^{3}\frac{x-x_j}{x_2-x_j}+y_3\times\prod\limits_{j=0,j\not=3}^{3}\frac{x-x_j}{x_3-x_j}\)
\(=\sum\limits_{i=0}^{3}y_i\prod\limits_{i\not=j}\frac{x-x_j}{x_i-x_j}\)
我们把界限设定为 \(n\),就可以得到常见的拉格朗日插值的式子:
\(f(x)=\sum\limits_{i=0}^{n}y_i\prod\limits_{j\not=i}\frac{x-x_j}{x_i-x_j}\)
此时,这道模板题我们就可以直接利用这个公式完成了。
附上代码:
/*
work by smyslenny
2021.06.27
P4781 【模板】拉格朗日插值
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iomanip>
#include <cstring>
#include <cstdlib>
#include <queue>
#include <vector>
#define int long long
#define INF 0x3f3f3f3f
using namespace std;
const int mod=998244353;
const int M=2e3+5;
int x[M],y[M];
int n,k,Ans;
int read()
{
register int x=0,y=1;
register char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=0;c=getchar();}
while(c>='0'&&c<='9') { x=x*10+(c^48),c=getchar();}
return y?x:-x;
}
int ksm(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
int ny(int a)
{
return ksm(a,mod-2);
}
signed main()
{
n=read(),k=read();
for(int i=1;i<=n;i++) x[i]=read(),y[i]=read();
for(int i=1;i<=n;i++)
{
int fz=y[i]%mod,fm=1;
for(int j=1;j<=n;j++)
{
if(i==j) continue;
fz=fz*(k-x[j])%mod;
fm=fm*(x[i]-x[j])%mod;
}
Ans=((Ans+fz*ny(fm)%mod)+mod)%mod;
}
printf("%lld\n",(Ans+mod)%mod);
return 0;
}
上面的方式的复杂度是 \(O(n^2)\) 的,对于一些题目中,给出的 \(x\) 的取值是连续的,那么此时我们可以将复杂度优化到 \(O(n)\)。
\(x\)取值连续时的优化
对于我们的式子,我们可以知道左边的求和 \(O(n)\) 是不能动的,我们考虑使右边的求积优化成 \(O(1)\) 的。
由于 \(x\) 是连续的,我们可以直接将式子转化成 \(f(x)=\sum\limits_{i=0}^ n y_i\prod\limits_{j\not=i}\frac{x-j}{i-j}\)。
对于分子,我们将其展开 \((x-1)\times(x-2)\times(x-3)\times\dots\times(x-(i-1))\times(x-(i+1))\times\dots\times(x-(j-1))\times(x-j)\)
我们维护一个关于 \(x\) 的前缀积和后缀积(类比前缀和),\(pre[i]=\prod\limits_{j=0}^i(x-j),suc[i]=\prod\limits_{j=i}^n(x-j)\)
分子就可以写成 \(pre[i-1]\times suc[i+1]\)。
再看分母,拆开
\(i\times(i-1)\times(i-2)\times(i-3)\times\dots\times (i-(i-1))\times(i-(i+1))\times\dots\times(i-n)\)
观察一下,\((i-(i-1))=1\) ,在这一块之前的可以看做是 \(1\) ~ \(i\) 的乘积,也就是 \(i!\) ,后面 \((i-(i+1))=-1\) 后面我们可以看做是 \(-1\backsim(i-n)\) 的阶乘,为了好计算,我们可以看作是 \(1\backsim(n-i)\) 的阶乘。
PS: 这里我们要注意正负号,当所乘的总数为奇数个时,需要带上负号,由于公式中不知道个数,下面默认为是正数,请不要认为就是正的。
所以分母可以化成 \(i!\times(n-i)!\)
右边也就可以化成 \(\frac{pre[i-1]\times suc[i+1]}{i!\times(n-i)!}\) ,分子和分母都可以 \(O(n)\) 预处理,查询是 \(O(1)\) 的,复杂度就可以优化成 \(O(n)\)。
一道模板题
附代码:
/*
work by smyslenny
2021.06.27
CF622F The Sum of the k-th Powers
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iomanip>
#include <cstring>
#include <cstdlib>
#include <queue>
#include <vector>
#define int long long
#define INF 0x3f3f3f3f
using namespace std;
const int M=1e6+5;
const int mod=1e9+7;
int n,k,tmp,Ans,pre[M],suc[M],fac[M];
int read()
{
register int x=0,y=1;
register char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=0;c=getchar();}
while(c>='0'&&c<='9') { x=x*10+(c^48),c=getchar();}
return y?x:-x;
}
void init()
{
pre[0]=suc[k+3]=fac[0]=1;
for(int i=1;i<=k+2;i++) pre[i]=pre[i-1]*(n-i)%mod;
for(int i=k+2;i>=1;i--) suc[i]=suc[i+1]*(n-i)%mod;
for(int i=1;i<=k+2;i++) fac[i]=fac[i-1]* i %mod;
}
int ksm(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
signed main()
{
n=read(),k=read();
init();
for(int i=1;i<=k+2;i++)
{
tmp=(tmp+ksm(i,k))%mod;
int fz=pre[i-1]*suc[i+1]%mod,fm=fac[i-1]*((k-i)&1?-1:1)*fac[k+2-i]%mod;
Ans=(Ans+tmp*fz%mod*ksm(fm,mod-2)%mod)%mod;
}
printf("%lld\n",(Ans%mod+mod)%mod);
return 0;
}
重心拉格朗日插值法
不难发现,当我们每插入一个值的时候,都需要推倒重算,这里可以用重心拉格朗日插值法来解决。
\(f(x)=\sum\limits_{i=0}^{n}y_i\prod\limits_{j\not=i}\frac{x-x_j}{x_i-x_j}\)
\(=\frac{\prod\limits_{i\not=j}x-x_j}{\prod\limits_{i!=j}x_i-x_j}\)
上下乘 \(x-x_i\)
\(=\sum\limits_{i=1}^{n}y_i\frac{\prod\limits_{i=1}^n x-x_j}{\prod\limits_{i\not=j}(x_i-x_j)\times(x-x_i)}\)
\(=\prod\limits_{i=1}^n (x-x_j)\sum\limits_{i=1}^{n}\frac{y_i}{\prod\limits_{i\not=j}(x_i-x_j)\times(x-x_i)}\)
设 \(\lambda=\prod\limits_{i=1}^n (x-x_j),\mu(x)=\prod\limits_{i\not=j}(x_i-x_j)\)
\(f(x)=\lambda\sum\limits_{i=1}^n\frac{y_i}{\mu(x)\times(x-x_i)}\)
插入一个值,只用 \(O(n)\) 更新 \(\mu(x)\) ,因为分子我们已经乘上 \((x-x_i)\) 了
询问一个值,\(O(n)\) 更新 \(\lambda\) ,再套公式即可。
参考资料:


