HDU 2475 BOX 动态树 Link-Cut Tree

Box

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

【Problem Description】

There are N boxes on the ground, which are labeled by numbers from 1 to N. The boxes are magical, the size of each one can be enlarged or reduced arbitrarily. Jack can perform the “MOVE x y” operation to the boxes: take out box x; if y = 0, put it on the ground; Otherwise, put it inside box y. All the boxes inside box x remain the same. It is possible that an operation is illegal, that is, if box y is contained (directly or indirectly) by box x, or if y is equal to x. In the following picture, box 2 and 4 are directly inside box 6, box 3 is directly inside box 4, box 5 is directly inside box 1, box 1 and 6 are on the ground.

The picture below shows the state after Jack performs “MOVE 4 1”:

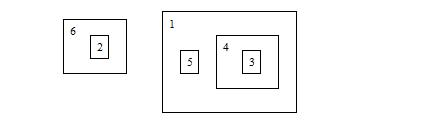
Then he performs “MOVE 3 0”, the state becomes:

During a sequence of MOVE operations, Jack wants to know the root box of a specified box. The root box of box x is defined as the most outside box which contains box x. In the last picture, the root box of box 5 is box 1, and box 3’s root box is itself.

 

【Input】

Input contains several test cases. For each test case, the first line has an integer N (1 <= N <= 50000), representing the number of boxes. Next line has N integers: a1, a2, a3, ... , aN (0 <= ai <= N), describing the initial state of the boxes. If ai is 0, box i is on the ground, it is not contained by any box; Otherwise, box i is directly inside box ai. It is guaranteed that the input state is always correct (No loop exists). Next line has an integer M (1 <= M <= 100000), representing the number of MOVE operations and queries. On the next M lines, each line contains a MOVE operation or a query:

1.  MOVE x y, 1 <= x <= N, 0 <= y <= N, which is described above. If an operation is illegal, just ignore it.

2.  QUERY x, 1 <= x <= N, output the root box of box x.

 

【Output】

For each query, output the result on a single line. Use a blank line to separate each test case.

 

【Sample Input】

2
0 1
5
QUERY 1
QUERY 2
MOVE 2 0
MOVE 1 2
QUERY 1
6
0 6 4 6 1 0
4
MOVE 4 1
QUERY 3
MOVE 1 4
QUERY 1

【Sample Output】

1
1
2

1
1

 

【题意】

动态地维护一些盒子套盒子的操作，询问根。

 

【分析】

盒子与盒子的关系可以直观地用树的结构来表示，一个结点下的子结点可以表示大盒子里面直接套着的小盒子。

所以本题就是一个裸的Link-Cut Tree模型了。

 

关于LCT树，还是推荐Yang Zhe的QTREE论文吧。 

动态树是用访问操作来划分树链，对于每一条树链，使用Splay来维护，用深度作为splay的左右关系。

 

看了很多代码，觉得还是写不好，总觉得别人的用起来不顺，最后是在自己原来Splay的基础上改的。

原本的整棵树是个splay，但是在LCT中，整棵树是由很多棵分散的Splay组合起来的，于是在其中的一些点上加上root标记，表示以这一点为根下面可以形成一棵splay树。多个这样的splay组合完成之后就是一棵LCT了。

 

后面的代码中加入了输入输出挂。。。。。。 

/* ***********************************************
MYID    : Chen Fan
LANG    : G++
PROG    : HDU 2475
************************************************ */

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

#define MAXN 50010

int sons[MAXN][2];
int father[MAXN],pathfather[MAXN],data[MAXN];
bool root[MAXN];
int spttail=0;

void rotate(int x,int w) //rotate(node,0/1)
{
    int y=father[x];
    
    sons[y][!w]=sons[x][w];
    if (sons[x][w]) father[sons[x][w]]=y;
    father[x]=father[y];
    if (father[y]&&(!root[y])) sons[father[y]][y==sons[father[y]][1]]=x;
    sons[x][w]=y;
    father[y]=x;

    if (root[y])
    {
        root[x]=true;
        root[y]=false;
    }
}

void splay(int x) //splay(node)
{
    while(!root[x])
    {
        if (root[father[x]]) rotate(x,x==sons[father[x]][0]);
        else 
        {
            int t=father[x];
            int w=(sons[father[t]][0]==t);
            if (sons[t][w]==x)
            {
                rotate(x,!w);
                rotate(x,w);
            } else 
            {
                rotate(t,w);
                rotate(x,w);
            }
        }
    }
}

void access(int v)
{
    int u=v;
    v=0;
    while(u)
    {
        splay(u);
        root[sons[u][1]]=true;
        sons[u][1]=v;
        root[v]=false;
        v=u;
        u=father[u];
    }
}

int findroot(int v)
{
    access(v);
    splay(v);
    while (sons[v][0]) v=sons[v][0];
    //splay(v,0);
    return v;
}

void cut(int v)
{
    access(v);
    splay(v);
    father[sons[v][0]]=0;
    root[sons[v][0]]=true;
    sons[v][0]=0;
}

void join(int v,int w)
{
    if (!w) cut(v);
    else 
    {
        access(w);
        splay(w);
        int temp=v;
        while(!root[temp]) temp=father[temp];
        if (temp!=w)
        {
            cut(v);
            father[v]=w;
        }
    }
}

int INT() 
{
    char ch;
    int res;
    while (ch=getchar(),!isdigit(ch));
    for (res = ch - '0';ch = getchar(),isdigit(ch);)
        res = res * 10 + ch - '0';
    return res;
}

char CHAR() 
{
    char ch, res;
    while (res = getchar(), !isalpha(res));
    while (ch = getchar(), isalpha(ch));
    return res;
}

int main()
{
    //freopen("2475.txt","r",stdin);
    
    int n;
    double flag=false;
    while(scanf("%d",&n)!=EOF)
    {
        if (flag) printf("\n");
        flag=true;

        memset(father,0,sizeof(father));
        memset(sons,0,sizeof(sons));
        for (int i=1;i<=n;i++) 
        {
            //scanf("%d",&father[i]);
            father[i]=INT();
            root[i]=true;
        }

        int m;
        m=INT();
        for (int i=1;i<=m;i++)
        {
            char s=CHAR();
            if (s=='M')
            {
                int x,y;
                x=INT();
                y=INT();
                join(x,y);
            } else 
            {
                int q;
                q=INT();
                printf("%d\n",findroot(q));
            }
        }
    }

    return 0;
}