密码学笔记(3)——分解因子算法

　　从前面两篇的内容可以知道对于RSA密码体制，最为明显的攻击方式就是试图分解模数。对于大整数分解目前最为有效的三种算法是二次筛法、椭圆曲线分解算法以及数域筛法，其他作为先驱的著名包括Pollard的$\rho$算法和$p-1$算法、Willian的$p+1$算法、连分式算法，当然还有试除法，这篇文章就根据课本的介绍总结这些算法。首先假定要分解的整数n为奇数。

一、试除法

　　试除法的思想是最为简单的，假设n为合数，那么它肯定有一个素因子满足$\rho \leq \lfloor \sqrt{n} \rfloor$，因此，只要利用$\lfloor \sqrt{n} \rfloor$的每个奇数去除n，这就足以判断n是素数还是合数。该算法在$n < 10^{12}$时还是不错的算法。

二、Pollard p-1算法

　　这个算法有两个输入，待分解的奇整数以及一个预先指定的阶B，本质来源是一个简单的数学证明，我们来先看看算法。

Alg1 Pollard p-1 Factoring Algorithm(n,B)

 $ a \leftarrow 2$ 

for $j \leftarrow 2$ to B

　　$a \leftarrow a^{j} mod \, n$

$d \leftarrow gcd(a-1 , n)$

if $1 < d < n$

　　then return(d)

else return("failure")

　　算法的证明过程如下，关键是在for循环中的操作以及之后的求最大公约数。假定p是n的一个素因子，又假定对每一个素数幂$q | (p-1)$，有$q \leq B$，那么在这种情形下必须有$$ (p-1) | B! \quad (因为B!包含有q)$$

　　在for循环结束时，我们有$$a \equiv 2^{B!} (mod \, n)$$

　　由于$p | n$，一定有$$a \equiv 2^{B!} (mod \, p)$$

　　现在，由Fermat定理可知$$2^{p-1} \equiv 1 (mod \, p)$$

　　由于$(p-1) | B!$可知，得$$a \equiv 1 (mod \, p)$$

　　因此有$p|(a-1)$，由于已经有$p|n$，可以看到$p | d$，其中$d = gcd(a-1 , n)$，因此整数d就是n的一个非平凡因子。

　　接下来要讨论的是B值，这个算法中，一共有B-1个模指数，利用“平方-乘”算法计算每一个模指数需要至多$2lbB$个模乘法，gcd的计算可以利用Euclidean算法在时间$o((logn)^{3})$内完成，因此整个算法的时间复杂度是$o(BlogB(logn)^{2}+(logn)^{3})$。如果B也是$o((logn)^{i})$，那么该算法就是关于$logn$的多项式时间算法，只是这样子选择的B，算法想要得到的d的概率是很小的。另一方面，如果B迅速增大，算法的执行效率不会比试除法快。

　　对于B值还要讨论的一个问题是，我们不能使B值太大，否则B!会是一个很可观的数字，换言之它要求对于p值不仅为n的素因子，而且$p-1$只有小的素因子。因此很容易构造出RSA模$n=pq$使得$p-1$分解算法失效。一般的方法是选择两个大素数$p_{1}$和$q_{1}$，使得$p = 2p_{1}+1$和$q=2q_{1}+1$也是素数，此时，RSA模$n=pq$将能抵抗$p-1$方法的分解。

 三、Pollard ρ算法

　　设p为n的最小素因子，假定存在两个整数$x，x^{'} \in Z_{n}$，使得$x \neq x^{'}$且$x \equiv x^{'} (mod \, p)$，那么有$p \leq gcd(x-x^{'} , n) < n$，所以，我们通过计算最大公因子得到n的一个非平凡因子，注意到并不需要事先知道p的值。

　　由于不知道p值，那么我们怎么选择这两个值呢，可以通过先选择一个随机子集$X \subseteq Z_{n}$来分解n，然后对所有不同的$x , x^{'} \in X$计算$gcd(x-x^{'},n)$，这个方法能够成功当且仅当映射$x \longrightarrow x (mod \, p)$对于$x \in X$得到至少一个碰撞，利用生日悖论，我们可以发现当X达到一定程度时，发生碰撞的概率还是非常大的。然而为了寻找这个碰撞，我们要计算$gcd(x-x^{'} , n)$，这就陷入了一个死循环，意味着，在找到p因子之前，至少要做$\binom{|x|}{2} > \frac{p}{2} $次的gcd。

 　　Pollard $\rho$算法集成了这个技巧的一个变形，仅仅需要较少的gcd计算，假定f为一个具有整系数的多项式，比如$f(x) = x^{2} + a$，其中a为一个小常数，假定映射$x \longrightarrow f(x) mod \, p$类似于一个随机映射，考虑序列$x_{1},x_{2},…,x_{n},…… \in Z_{n}$其中有$$x_{j} = f(x_{j-1}) mod \, n$$对于所有的$j \geq 2$，令m为一个整数，且定义$X=\{ x_{1},x_{2},…,x_{m} \}$，为了简单起见，假定X直接包含了m个不同的模n剩余，希望X为$Z_{n}$的m个元素的随机子集。

　　我们来寻找两个不同的值$x_{i},x_{j} \in X$使得$gcd(x_{j} - x_{i} , n) > 1$，每次计算序列中的一个新项$x_{j}$，对所有的$i < j$计算$gcd(x_{j} - x_{i},n)$，这样子就做到了大大减少gcd计算的次数，但是要证明一下为什么可以这么做。

　　假定$x_{i} \equiv x_{j} (mod \, p)$，利用f为整系数多项式这个事实，有$f(x_{i}) \equiv f(x_{j}) (mod \, p)$，由于$x_{i+1} = f(x_{i}) (mod \, n)$且$x_{j+1} = f(x_{j}) (mod \, n)$，那么有$$x_{i+1} mod \, p = (f(x_{i}) mod \, n)mod \, p = f(x_{i}) mod \, p$$因为$p | n$，类似的$$x_{j+1} mod \, p = f(x_{j}) mod \, p$$因此有$x_{i+1} \equiv x_{j+1} (mod \, p)$。重复上述过程就可以得到结论:

　　如果$x_{i} \equiv x_{j} (mod \, p)$，那么有$x_{i+ \delta} \equiv x_{j + \delta} (mod \, p)$，对于所有的整数$\delta \geq 0$，记$l = j - i$，得到$x_{i^{'}} \equiv x_{j^{'}} (mod \, p)$如果$ j^{'} > i^{'} \geq i$且$j^{'} - i^{'} \equiv 0 (mod \, l)$。

　　假定我们利用顶点集$Z_{p}$构造一个图G，其中对于$ i \geq 1$，从点$x_{i} (mod \, p)$向点$x_{i+1} (mod \, p)$做一条边，存在第一个点对$x_{i},x_{p}$且$i < j$使得$x_{i} \equiv x_{j} (mod \, p)$，因此可以构造出这样子的一个图$$x_{1} (mod \, p) \rightarrow x_{2} (mod \, p) \rightarrow x_{3} (mod \, p) \rightarrow … \rightarrow x_{i} (mod \, p) $$ $$  x_{i} (mod \, p) \rightarrow x_{i+1} (mod \, p) \rightarrow x_{i+2} (mod \, p) \rightarrow …… \rightarrow x_{j} (mod \, p) \rightarrow x_{i} (mod \, p) $$

　　从而这条链看上去就是一个字母$\rho$。

　　

 

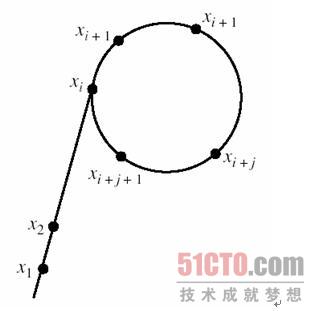
　　通常在算法中会取$j  = 2i$来寻找碰撞，算法如下所示。

Alg2 Pollard $\rho$ Factoring Algorithm(n,x_{1})

external f

$x \leftarrow x_{1}$

$x^{'} \leftarrow f(x) mod \, n$

$p \leftarrow gcd(x - x^{'} , n)$

while p = 1

　　// in the ith iteration, $x = x_{i}$ and $x^{'} = x_{2i}$

　　$x \leftarrow f(x) (mod \, n)$

　　$x^{'} \leftarrow f(x^{'}) (mod \, n)$

　　$p \leftarrow gcd(x - x^{'} , n)$

if $p = n$

　　then return ("failure")

　　else return (p)

　　前面有$l = j - i$，如果$x_{i} \equiv x_{j} (mod \, p)$，那么对于所有满足$i^{'} \equiv 0 (mod \, l)，i^{'} \geq i$有$x_{i^{'}} \equiv x_{(2i)^{'}} (mod \, l)$，在$l$个连续整数$i,i+1,…,j-1$，必然存在一个数可以被$l$整除，满足上面两个最小值$i^{'}$不超过$j-1$，因此找到一个因子$p$的循环次数最多为$j$，而$j$的值最大为$\sqrt{p}$。换言之，对于很大的数，只要找到那个圈，就意味着成功。

　　算法可能因为没有找到n的非平凡因子而失败，当且仅当找到$x \equiv x^{'} (mod \, n)$，这等价于$x = x^{'}$，这种情况发生的概率大致为$\frac {p}{n}$，当n很大时这种情况概率变得很小，这时候可以选择一个不同的初值重新运行或者选择一个不同的函数f。

四、Dixon的随机平方算法

　　这个分解因子算法的理论是基于如下的简单事实，假定我们可以找到$x \neq \pm y (mod \, n)$使得$x^{2} \equiv y^{2} (mod \, n)$，那么有$$ n | (x+y)(x-y)$$，但是$x-y$和$x+y$均不能被n整除，换言之，这两个式子中必然至少有一个使得$gcd(f , n) > 1 f=x+y 或者f =x-y$。

　　随机平方算法使用一个因子基B，它是b个最小素数的集合(b是适当选取的数值)，首先得到几个整数z，使得$z^{2} (mod \, n)$的所有素因子都在B中，将某些z相乘使得每一个在B中的素数出现偶数次，这样就建立起了一个所期望的类型的同余方程$x^{2} \equiv y^{2}(mod \, n)$，这个方程可能导出n的一个分解。

　　说起来很复杂，需要举一个被仔细设计的例子来配合说明。

Exm3 假定n=15770708441，令$b=6$，那么$B=\{ 2,3,5,7,11,13 \}$，考虑如下三个同余方程$$ \begin{align} 8340934156^{2} & \equiv 3×7(mod \, n) \\ 12044942944^{2} & \equiv 2×7×13(mod \, n) \\ 2773700011^{2} & \equiv 2×3×13(mod \, n) \\ \end{align} 

如果取上面同余方程两边的乘积，有$$(8340934156×12044942944×2773700011)^{2} \equiv (2×3×7×13)^{2}(mod \, n)$$

在两边表达式的括号模n约化，有$$9503435785^{2} \equiv 546^{2}(mod \, n)$$

利用Euclidean算法，计算$$gcd(9503435785-546,15770708441) = 115759$$得出$n$的因子115759。

　　下面来说明当已经有这些整数z的时候，怎么构造相乘式子使得因子基中的素数出现偶数次，假定$B=\{ p_{1},…,p_{b} \}$为因子基，设$c$为稍大于$b$的整数，且假定已经得到了$c$个同余方程：$$z_{j}^{2} \equiv p_{1}^{\alpha_{1j}} × p_{2}^{\alpha_{2j}}× p_{3}^{\alpha_{3j}} ×… × p_{b}^{\alpha_{bj}} (mod \, n)$$

 　　其中$1 \leq j \leq c$，对于每一个$j$，考虑向量$$a_{j} = (\alpha_{1j} mod \, 2,…,\alpha_{bj} mod \, 2) \in (Z_{2})^{b}$$

　　如果我们可以找到$a_{j}$的子集使得其模2的和为向量(0,…,0)，那么对应的$z_{j}$的乘积将会使得B中的每个因子偶数次。

　　于是，问题就转化成寻找$c$个向量$a_{1},…,a_{c}$的一个子集使得其和模2为零向量，即找一个线性相关，当$c>b$时，这样的线性相关一定存在，我们选取$c>b+1$(c为稍大于b的整数)的原因是，不能保证任一给定的同余方程$x^{2} \equiv y^{2} (mod \, n)$一定能得到n的分解。从上一篇的定理告诉我们，假定$x^{2} \equiv y^{2} \equiv a (mod \, n)$，其中$gcd(a,n) = 1$，那么$a$有$2^{l}$个模$n$的平方根，其中$l$为$n$的素因子的个数，如果$l \geq 2$，那么$a$至少有4个平方根，如果x和y随机选取，那么$x \equiv \pm y(mod \, n)$出现的概率最多为$\frac {1}{2}$。

　　有了这个估计，我们希望根据这些形如$x^{2} \equiv y^{2} (mod \, n)$并且$x \neq \pm y(mod \, n)$，得到$n$的一个非平凡因子，这根本的来源是要如何选取整数z，一种方法是简单随机选择z，另一种是试用形如$j + \lceil \sqrt{kn} \rceil$和形如$\lfloor \sqrt{kn} \rfloor$的整数，其中$j = 0 , 1 ,2 , …，k =1,2,…$

 　　最后一个问题就是，因子基要选取多大，显然，当b越大时，似乎更有可能找到B上的分解，但是带来的问题是同余式会很多，我们需要一些数论中的结果帮助选取b的值。

Def4 (m-光滑)假定n和m为正整数，我们称n是m光滑的，如果n的任何一个素因子都小于等于m，并且同时定义$\psi (n,m)$定义为小于等于n且是m光滑的正整数的个数。

　　数论当中有一个重要的结果列举如下。

Thm5 如果$n >> m$，那么有$$\frac {\psi (n,m)}{n} \approx \frac{1}{u^{u}}$$其中有$u = \frac {log n}{log m}$，注意到$\frac {\psi (n,m)}{n}$表示从集合$\{ 1,…, n \}$中随机选取一个整数为m-光滑的概率。

　　假定$n \approx 2^{r}$和$m \approx 2^{s}$，那么有$$u= \frac{logn}{logm} \approx \frac{r}{s}$$一个$r$比特的整数除以一个$s$比特的整数的执行时间为$o(rs)$，如果假定了$r<m$，可以在时间$o(rsm)$内判断集合$\{ 1,2,…,n \}$中一个整数是否为$m$光滑的。

　　因子基B可以选取为包含了所有小于等于m的素数，应用素数定理，我们有$$|B| = b = π(m) \approx \frac{m}{ln m}$$为了算法成功，需要找出略多于$b$个的$m$光滑的模$n$平方数，我们期望测试$bu^{u}$个整数就可以得到$b$个$m$光滑的整数，因此，找到所需$m$光滑的平方数的期望时间为$o(bu^{u}×rsm)$，我们已经有$b$为$o(\frac{m}{s})$，算法的第一部分运行时间为$o(rm^{2}u^{u})$

　　在算法的第二部分，需要化简模2的系列矩阵，构造出形如$x^{2} \equiv y^{2} (mod \, n)$的同余式，再应用欧几里得算法，这几步所需的时间是$r$和$m$的多项式，即$o(r^{i}m^{j})$

　　现在，我们给定了$n \approx 2^{r}$和$m \approx 2^{s}$，上面是针对$n$进行的优化，下面对$m$进行优化，一个好的选择是取$s \approx \sqrt{rlbr}$，那么有$$u \approx \frac{r}{s} \approx \sqrt{\frac{r}{lbr}}$$现在开始估计

　　$$\begin{align} lbu^{u} =& ulbu \\ \approx & \sqrt{\frac{r}{lbr}} lb \lgroup \sqrt{\frac{r}{lbr}} \rgroup \\ < &  \sqrt{\frac{r}{lbr}} lb \sqrt{r} \\ = & \sqrt{\frac{r}{lbr}} × \frac{lbr}{2} \\ = & \frac{\sqrt{rlbr}}{2} \\ \end{align}$$

　　于是有$$u^{u} \leq 2^{0.5 \sqrt{rlbr}}$$

　　因此，所有的运行时间可以写成如下形式$$o(2^{c \sqrt{rlbr}})$$其中$c$为一个常数，再利用$r \approx lb n$，最终可以导出如下通常的期望时间为$o(e^{(1+o(1))\sqrt{lnn lnlnn}})$。

五、实际中的分解因子算法

　　二次筛法的来源于判断$z^2 (mod \, n)$在B上的分解的一个筛法过程，数域筛法是构造同余式$x^{2} \equiv y^{2} (mod \, n)$来分解n，但这是在代数整数环中进行计算的，二次筛法、椭圆筛法和数域筛法的渐进运行时间均有上面讨论的形式，详细可以寻找更多的参考文献。

　　在下一篇文章中，我们讨论除了分解$n$以外是否有其他体制对RSA密码体制进行攻击。