Stack实现表达式的求值

1.用栈求中缀表达式的值：

建立2个栈，S1暂存操作数，S2暂存运算符，当遇到操作数则入S1，遇到运算符准备入S2，首先若S2为空或者S2栈顶为'('，则运算符直接入S2栈，若S2不空并且S2栈顶非'('，若当前扫描运算符的运算优先级大于栈顶运算符优先级,则入栈S2，否则对S2不停地执行出栈操作，每出栈一个运算符就同时从S1出栈2个操作数，先出栈的排在右边，后出战的排在左边，然后拿这2个操作数与运算符进行运算并将结果存入S1

int getPriority(char a){
    if(a == '+' || a=='-'){
        return 0;
    }else{
        return 1;
    }
}
int calSub(float opand1,char op,float opand2,float &result){
    if(op == '+')     result =opand1+opand2;
    if(op == '-')    result =opand1-opand2;
    if(op == '*')    result=opand1*opand2;
    if(op == '/'){
        if(fabs(opand2)<MIN){
            return 0;
        }else{
            result=opand1/opand2;
        }
    }
    return 1;    
}
int calStackTopTwo(float s1[],int &top1,char s2[],int &top2){
    float opand1,opand2,result;
    char op;
    int flag;
    opand2=s1[top1--];
    opand1=s1[top1--];
    op=s2[top2--];
    flag=calSub(opand1,op,opand2,result);
    if(flag == 0){
        cout<<"ERROR"<<endl;
        return 0;
    }
    s1[++top1]=result;
    return flag;
}
float calInfix(char exp[]){
    float s1[MaxSize]; int top1=-1;
    char s2[MaxSize]; int top2=-1;
    int i=0;
    while(exp[i]!='\0'){
        if('0'<=exp[i] && exp[i]<='9'){
            s1[++top1]=exp[i]-'0';
            ++i;
        }else if(exp[i] == '('){
            s2[++top2]='(';
            ++i;
        }else if(exp[i] == '+'||exp[i] =='-'||exp[i]=='*'||exp[i]=='/'){
            if(top2 == -1 ||s2[top2] =='('||getPriority(exp[i])>getPriority(s2[top2])){
                s2[++top2]=exp[i];
                ++i;
            }else{
                int flag=calStackTopTwo(s1,top1,s2,top2);
                if(flag == 0){
                    return 0;
                }
            }
        }else if(exp[i] ==')'){
            while(s2[top2] !='('){    
                int flag=calStackTopTwo(s1,top1,s2,top2);
                if(flag == 0){
                    return 0;
                }
            }
            --top2;//左括号丢掉
            ++i; 
        }
    }
    while(top2!=-1){
        int flag=calStackTopTwo(s1,top1,s2,top2);
        if(flag == 0){
            return 0;
        }
    }
    return s1[top1];
}

2.用Stack求后缀表达式的值

 

 

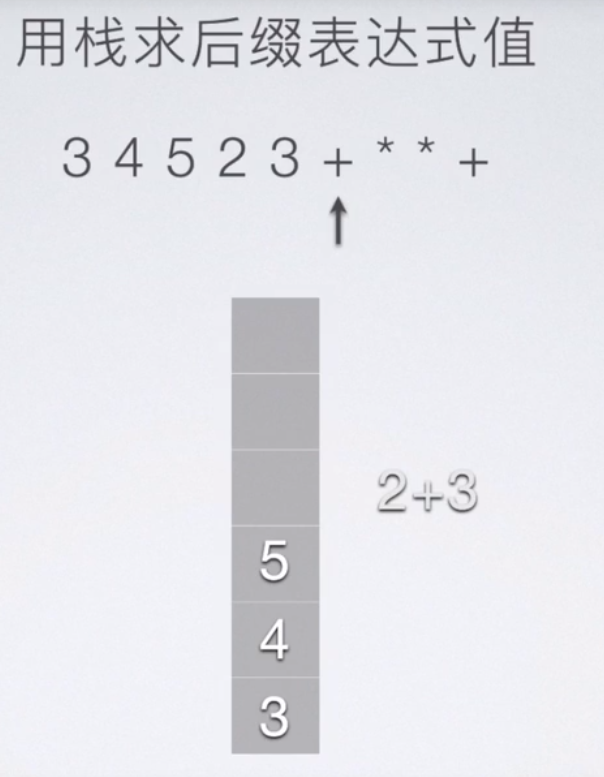
int calSub(float opand1,char op,float opand2,float &result){
    if(op == '+')     result =opand1+opand2;
    if(op == '-')    result =opand1-opand2;
    if(op == '*')    result=opand1*opand2;
    if(op == '/'){
        if(fabs(opand2)<MIN){
            return 0;
        }else{
            result=opand1/opand2;
        }
    }
    return 1;    
}
float calPostFix(char exp[]){
    float s[MaxSize];int top=-1;for(int i=0;exp[i]!='\0';++i){
        if('0'<=exp[i] &&exp[i]<=9){
            s[++top]=exp[i]-'0';
        }else{
            float opnd1,opnd2,result;
            char op;
            int flag;
            opnd2=s[top--];
            opnd1=s[top--];
            op=exp[i];
            flag=calSub(opnd1,op,opnd2,result);
            if(flag == 0){
                cout<<"ERROR"<<endl;
            }
            s[++top]=result;
        }    
    }
    return s[top];
}

3.用Stack求前缀表达式的值

不同点：从右往左扫描，先出栈的排左边，后出栈的排右边。

float calPreFix(char exp[],int len){
    float s[MaxSize];int top=-1;
    int i=len-1;
    for(i;i>=0;i--){
        if('0'<=exp[i] &&exp[i]<=9){
            s[++top]=exp[i]-'0';
        }else{
            float opnd1,opnd2,result;
            char op;
            int flag;
            opnd2=s[top--];
            opnd1=s[top--];
            op=exp[i];
            flag=calSub(opnd2,op,opnd1,result);
            if(flag == 0){
                cout<<"ERROR"<<endl;
            }
            s[++top]=result;
        }    
    }
    return s[top];
}