最短路径算法总结（啊哈！算法）

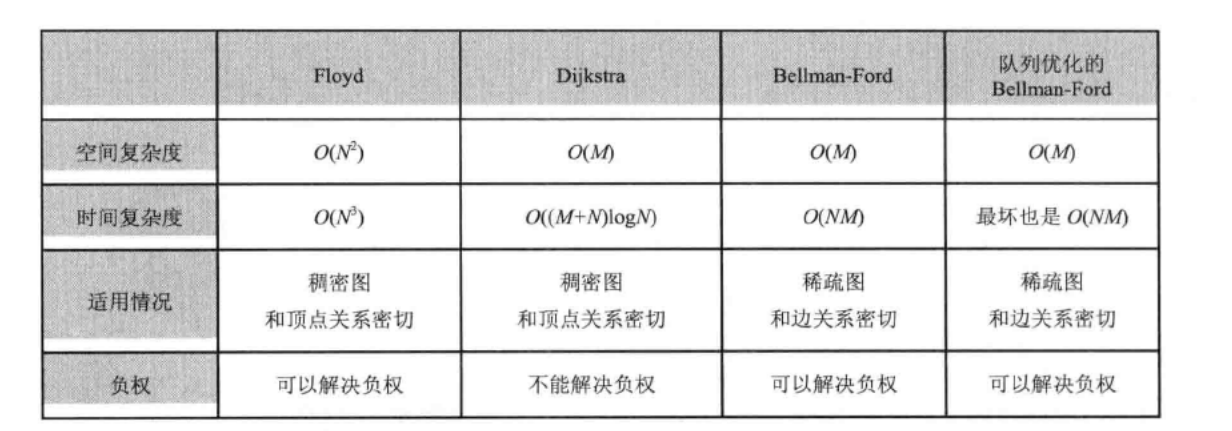
1.Floyd:

求任意两点的最短路径：i号顶点到j号顶点只经过前k个顶点的最短路径

时间复杂度O（N^3）

#include<iostream>
using namespace std;
int e[10][10];
int inf=999999;
int n,m;
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i == j){
                e[i][j]=0;
            }else{
                e[i][j]=inf;
            }
        }
    }
    for(int i=1;i<=m;i++){
        int a,b,c;
        cin>>a>>b>>c;
        e[a][b]=c;
    }
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(e[i][j]>e[i][k]+e[k][j] && e[i][k]<inf && e[k][j]<inf){
                    e[i][j]=e[i][k]+e[k][j];
                }
            }
        }
    }
    cout<<endl;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(j!=n){
                cout<<e[i][j]<<' ';
            }else{
                cout<<e[i][j]<<endl;
            }
        }
    }
    return 0;
}

 

 

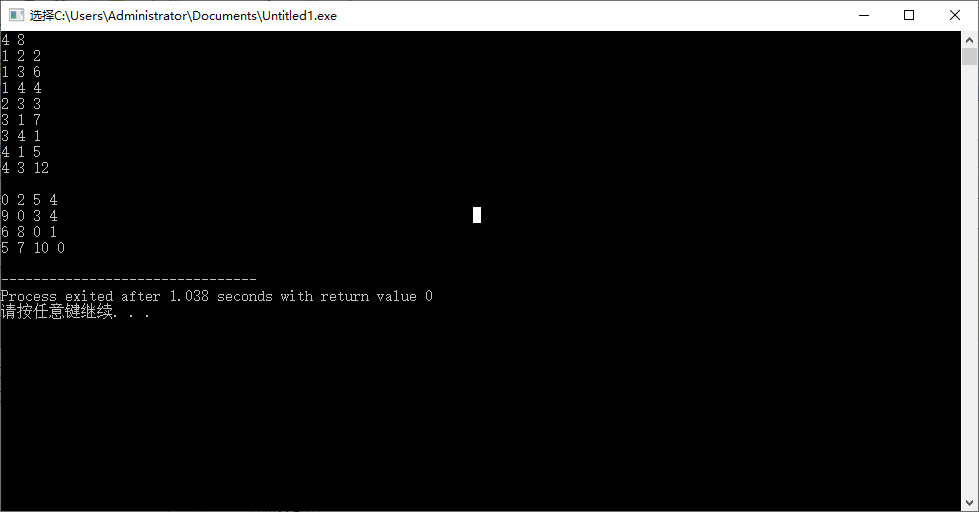
2.Dijkstra

单源最短路径算法

时间复杂度O(N^2)

#include<iostream>
using namespace std;
int e[20][20],dis[20],book[20];
int min1,n,m,u;
int inf=999999;
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i == j){
				e[i][j]=0;
			}else{
				e[i][j]=inf;
			}
		}
	}
	for(int i=1;i<=m;i++){
		int a,b,c;
		cin>>a>>b>>c;
		e[a][b]=c;
	}
	for(int i=1;i<=n;i++){
		dis[i]=e[1][i];
	}
	book[1]=1;
	for(int i=1;i<=n-1;i++){
		min1=inf;
		for(int j=1;j<=n;j++){
			if(!book[j] && dis[j]<min1){
				min1=dis[j];
				u=j;
			}
		}
		book[u]=1;
		for(int v=1;v<=n;v++){
			if(dis[v] > dis[u]+e[u][v]){
				dis[v]=dis[u]+e[u][v];
			}
		} 
	}
	for(int i=1;i<=n;i++){
		cout<<dis[i]<<' ';
	}
	return 0;
}

 

 

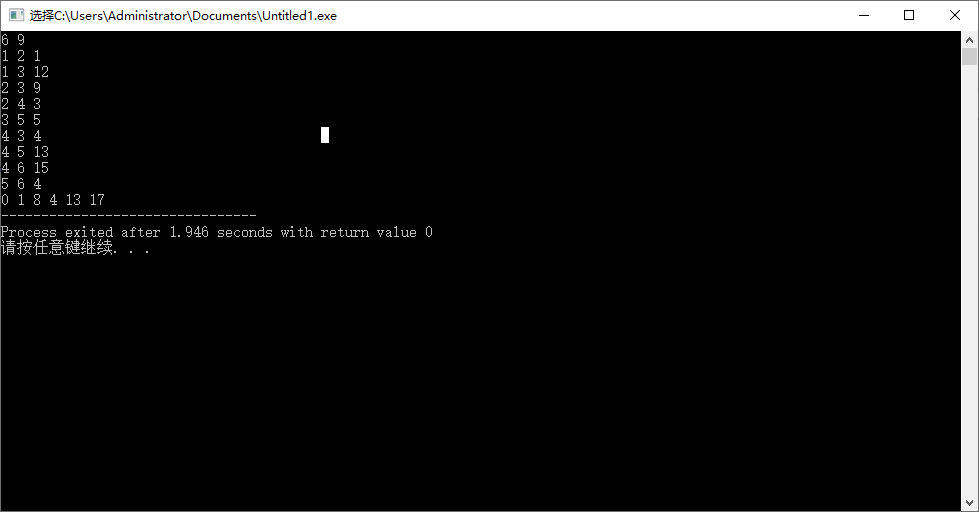
3.Ballman-Ford

 

#include<iostream>
using namespace std;
int e[50][50],book[50],dis[50],back[50];
int u[50],v[50],w[50];
int first[50],next[50];
int n,m,check,flag;
int inf=999999;
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        first[i]=-1;
    }
    for(int i=1;i<=m;i++){
        cin>>u[i]>>v[i]>>w[i];
        next[i]=first[u[i]];
        first[u[i]]=i;
    }
    for(int i=1;i<=n;i++){
        dis[i]=inf;
    }
    dis[1]=0;
    for(int k=1;k<=n-1;k++){
        for(int i=1;i<=n;i++){
            back[i]=dis[i];
        }
        for(int i=1;i<=m;i++){
            if(dis[v[i]]>dis[u[i]]+w[i]){
                dis[v[i]]=dis[u[i]]+w[i];
            }
        }
        for(int i=1;i<=n;i++){
            if(back[i]!=dis[i]){
                flag=1;
                break;
            }
        }
        if(flag == 0){
            break;
        }        
    }
    for(int i=1;i<=m;i++){
        if(dis[v[i]] >dis[u[i]] + w[i]){
            check=1;
        }
    }
    cout<<endl;
    if(check){
        cout<<"有负权边"<<endl;
    }else{
        cout<<"NO!"<<endl;
    }
    for(int i=1;i<=n;i++){
        if(i!=n){
            cout<<dis[i]<<' ';
        }else{
            cout<<dis[i]<<endl;
        }
    }
    return 0;

} 

 

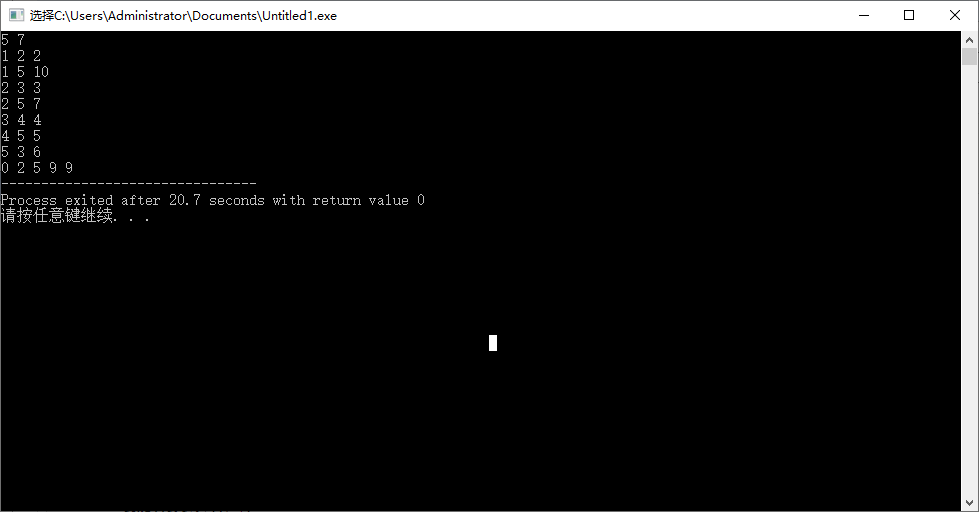
4.Ballman-ford队列优化

每次仅仅对最短路径估计值发生变化的点的出边进行"松弛"操作。

#include<iostream>
using namespace std;
int dis[20],first[20],next[20],u[20],v[20],w[20],book[20];
int n,m,inf=999999;
int que[100],head,tail;
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        first[i]=-1;
    }
    for(int i=1;i<=m;i++){
        cin>>u[i]>>v[i]>>w[i];
        next[i]=first[u[i]];
        first[u[i]]=i;
    }
    for(int i=1;i<=n;i++){
        dis[i]=inf;
    }
    dis[1]=0;
    head=tail=1;
    que[tail]=1;
    tail++;
    book[1]=1;
    while(head!=tail){
        int k=first[que[head]];
        while(k!=-1){
            if(dis[v[k]]>dis[u[k]]+w[k]){
                dis[v[k]]=dis[u[k]]+w[k];
            }
            if(!book[v[k]]){
                book[v[k]]=1;
                que[tail]=v[k];
                tail++;
            }
            k=next[k];
        }
        head++;
    }
    for(int i=1;i<=n;i++){
        cout<<dis[i]<<' ';
    }
    return 0;
}

 5.对比总结