简单概念

引理1：如果a, b, c是任意三个整数，m是一个正整数，则当a=b(mod m),b=c(mod m) 成立时，有a=c(mod m)
引理2：如果a, b, c是任意三个整数，m是一个正整数，且(m, c)=1,则当ac=bc(mod m)时，有a=b(mod m).
引理3：如果a, b是任意两个整数，而m, n是两个正整数，则当a=b(mod m)时，有a^n=b^n(mod m).
引理4：设m是一个大于1的整数，a1, a2, a3,....am是模m的一个完全剩余系。则在a1, a2, a3 ....am中任取两个整数，则这两个整数对模m是不同余的。
引理5：设m是一个大于1的整数，而a1, a2, ....am是m个整数，有设在a1, a2, ...am中任取出两个整数时，这两个对模m是不同余的，则a1, a2, ...am是模m的一个完全剩余系。
引理6：设m是一个大于1的整数，而a1, a2, ...am是模m的一个完全剩余系，则当b是一个整数时，a1+b，a2+b....am+b也是模m的一个完全剩余系。
引理7：设m是一个大于1的整数，b是一个整数且满足条件（b, m）=1，如果a1, a2,...am是模m的一个完全剩余系，则ba1,ba2...bam也是模m的一个完全剩余系。
引理8：设m是一个大于1的整数，而b, c是两个任意的整数但满足条件（b, m）=1,如果a1, a2,...am是模m的一个完全剩余系，则ba1+c, ba2+c....bam+c也是模m的一个完全剩余系。
引理9：如果m是一个大于1的整数而a, b是任意的两个整数，使得a=b(mod m)成立，则有（a, m)=(b, m).
引理10：设L是一个正整数，p是一个素数，则我们有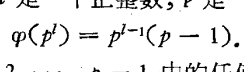
引理11：设m是一个大于1的整数，b1, b2...bm是一个模m的一个简化剩余系，如b1, b2...bm中任取出两个整数，则这两个整数对模m是不同余的，如在b1,b2...bm中任取出一个整数，则这个整数是和m互素的。
引理12：设m是一个大于1的整数，b2,b2...bm是 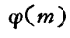个和m互素的整数，又设在b1, b2...bm中取出两个整数时，这两个整数对模m是不同余的，则b1, b2...bm是模m的一个简化剩余系。
引理13：设m是一个大一1的整数，a是一个整数且满足条件（a,m)=1.如果b1, b2.. bm。是模m的一个简化剩余系则ab1, ab2,... abm也是模m的一个简化剩余系。