C++U7-10-最小生成树
本节课作业讲解视频：
链接：https://pan.baidu.com/s/1lLlmhShdat9HuJWx7Rp_tA?pwd=0000
提取码：0000
最小生成树是一种在无向图中寻找特定结构的算法结果，它具有多种实际应用。以下是关于最小生成树的一些主要应用：
- 网络布局问题：
- 在一个连通加权无向图中，最小生成树算法可以帮助找到一个包含所有顶点的最小权重树，从而在地图上实现有效的布局。这种布局能够确保连接所有点的路径的总成本最低。
- 地图着色问题：
- 在地图着色问题中，最小生成树算法可以用于优化颜色分配。通过构建最小生成树，可以确保相邻区域的颜色不同，同时最小化所需的颜色数量。
- 车辆路径优化问题：
- 在物流和运输行业中，最小生成树算法被用于优化车辆的行驶路径。这有助于降低运输成本，使车辆能够更高效地完成配送任务。
- 通信网络设计：
- 在设计通信网络时，最小生成树算法有助于构建高效的数据传输网络。这种网络能够在不同的节点之间快速传输数据，同时确保传输成本最低。
- 电力系统设计：
- 在电力系统的设计中，最小生成树算法被用于构建高效的输电网络。它确保了电能从发电厂到各个用户的传输过程中损耗最小。
- 城市光缆铺设：
- 当需要在多个城市之间铺设光缆时，最小生成树算法可以帮助找到一种方案，使得所有城市之间都能实现通信，并且铺设光缆的总费用最低。
总结来说，最小生成树算法在多个领域都有广泛的应用，特别是在需要优化连接成本或传输效率的场合。通过构建最小生成树，可以确保在满足连通性的同时，实现成本的最小化。
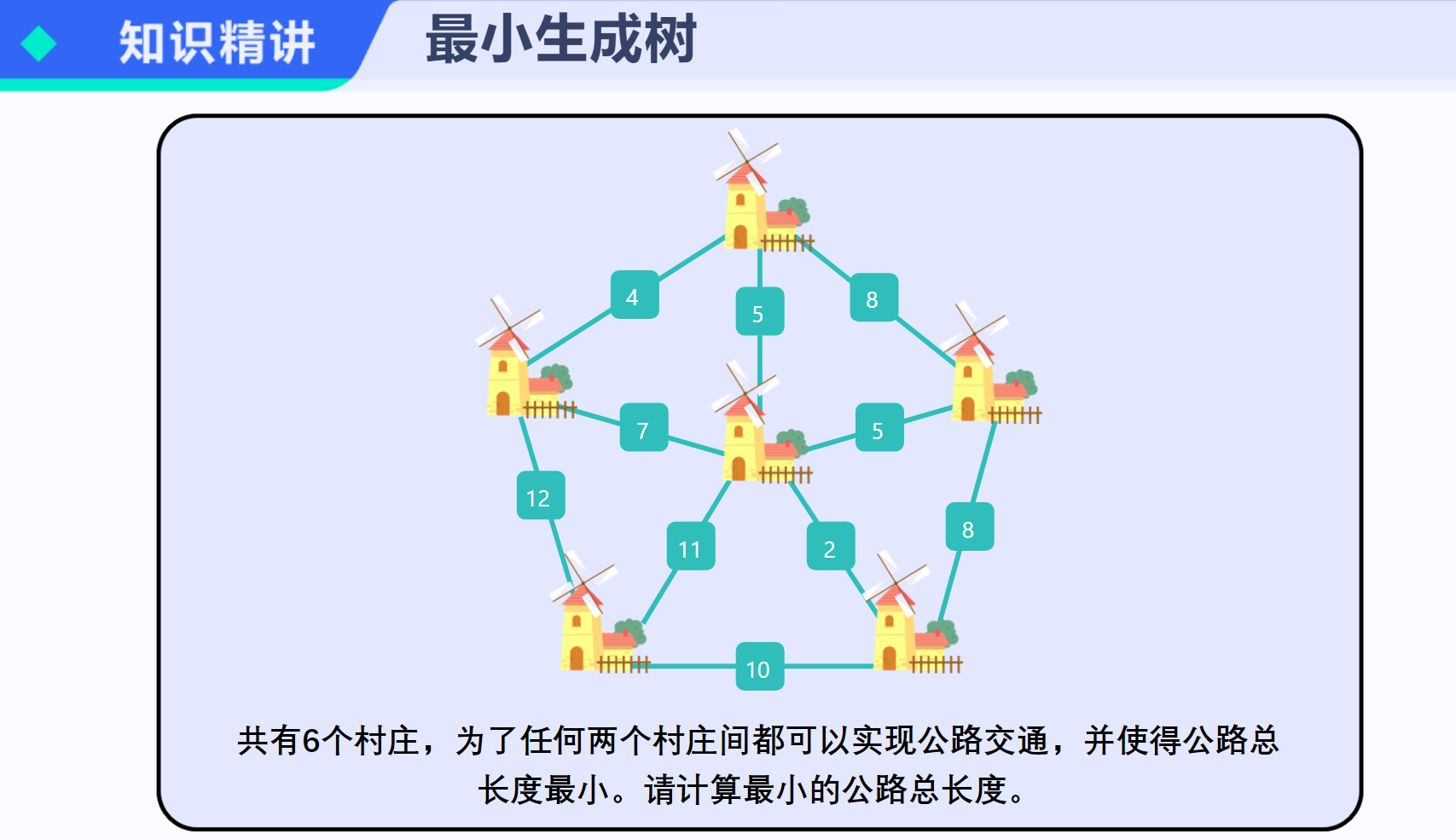
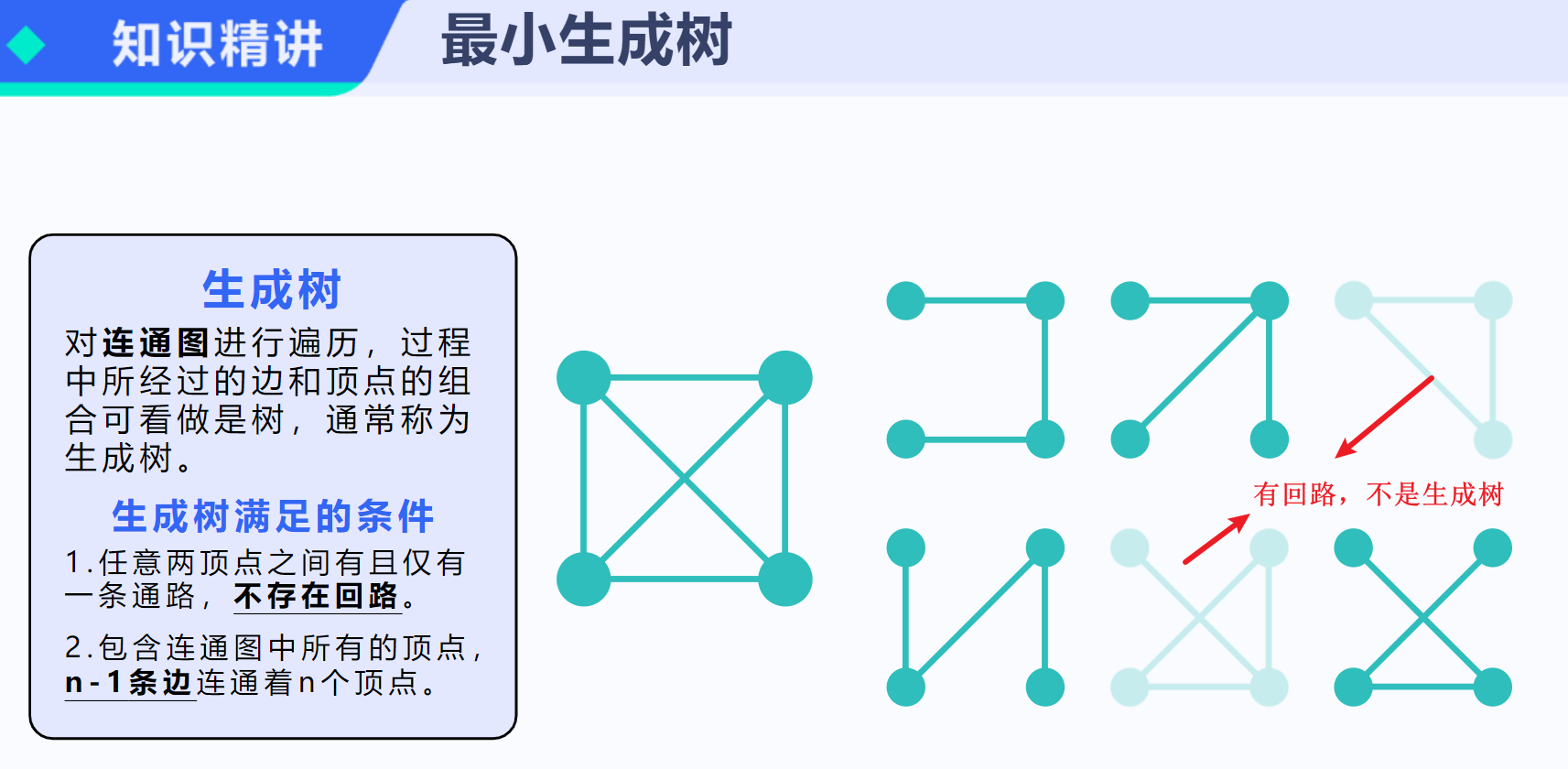
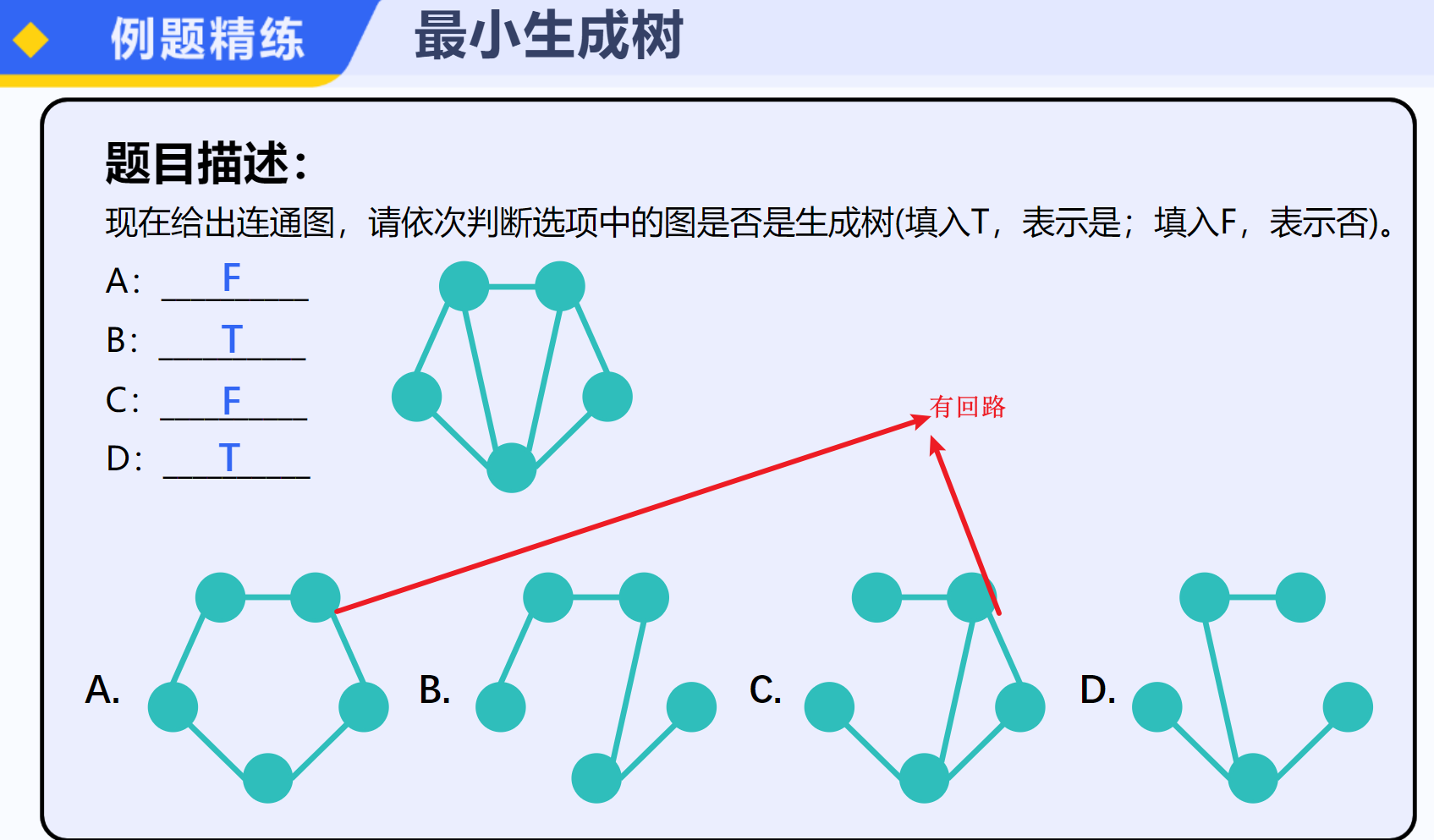
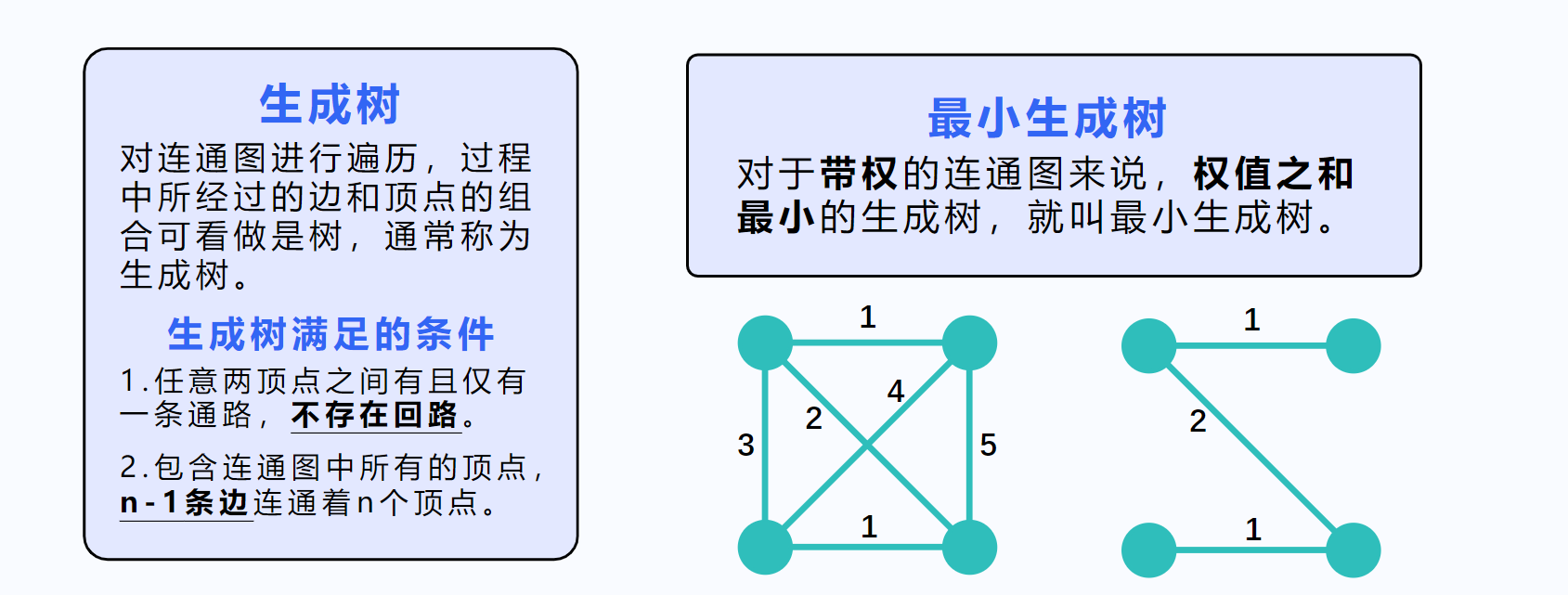
Kruskal算法是一种用于解决最小生成树问题的贪心算法。最小生成树是一个无向连通带权图的一棵子图，它包含原图中的所有顶点，并且所有的边都是原图中的边，同时子图中边的权值之和最小。
Kruskal算法的基本思想是按照边的权值从小到大进行排序，然后从中选择边，但选择的边不能形成一个环。算法步骤如下：
- 初始化：创建一个空的图G'，该图包含原图G的所有顶点，但没有任何边。
- 创建一个空的集合S，用于存放已选择的边。
- 对原图G中的所有边按照权值进行升序排序。
- 遍历排序后的边列表，对于每条边e(u, v)：
a. 如果顶点u和v在当前的图G'中不连通（即它们不在同一个连通分量中），则将边e添加到图G'和集合S中。
b. 如果顶点u和v在当前的图G'中已经是连通的（即它们在同一个连通分量中），则跳过边e，不将其添加到图G'和集合S中。 - 重复步骤4，直到图G'包含n-1条边（n是顶点的数量），或者所有的边都已经遍历过。
- 最终的图G'就是原图G的最小生成树，集合S中的边就是最小生成树的边集。
为了判断两个顶点是否在同一连通分量中，可以使用并查集（Union-Find）数据结构。并查集可以高效地处理一些不交集的合并及查询问题。在Kruskal算法中，并查集用于判断添加某条边后是否会形成环。
需要注意的是，Kruskal算法的时间复杂度主要取决于边的排序，因此其时间复杂度为O(mlogm)，其中m是边的数量。如果使用Fibonacci堆来优化查找最小边的操作，时间复杂度可以降低到O(mloga)，其中a是边的权值的最大值与最小值之比。然而，在实际应用中，由于排序操作的高效性，简单的排序通常已经足够快了。
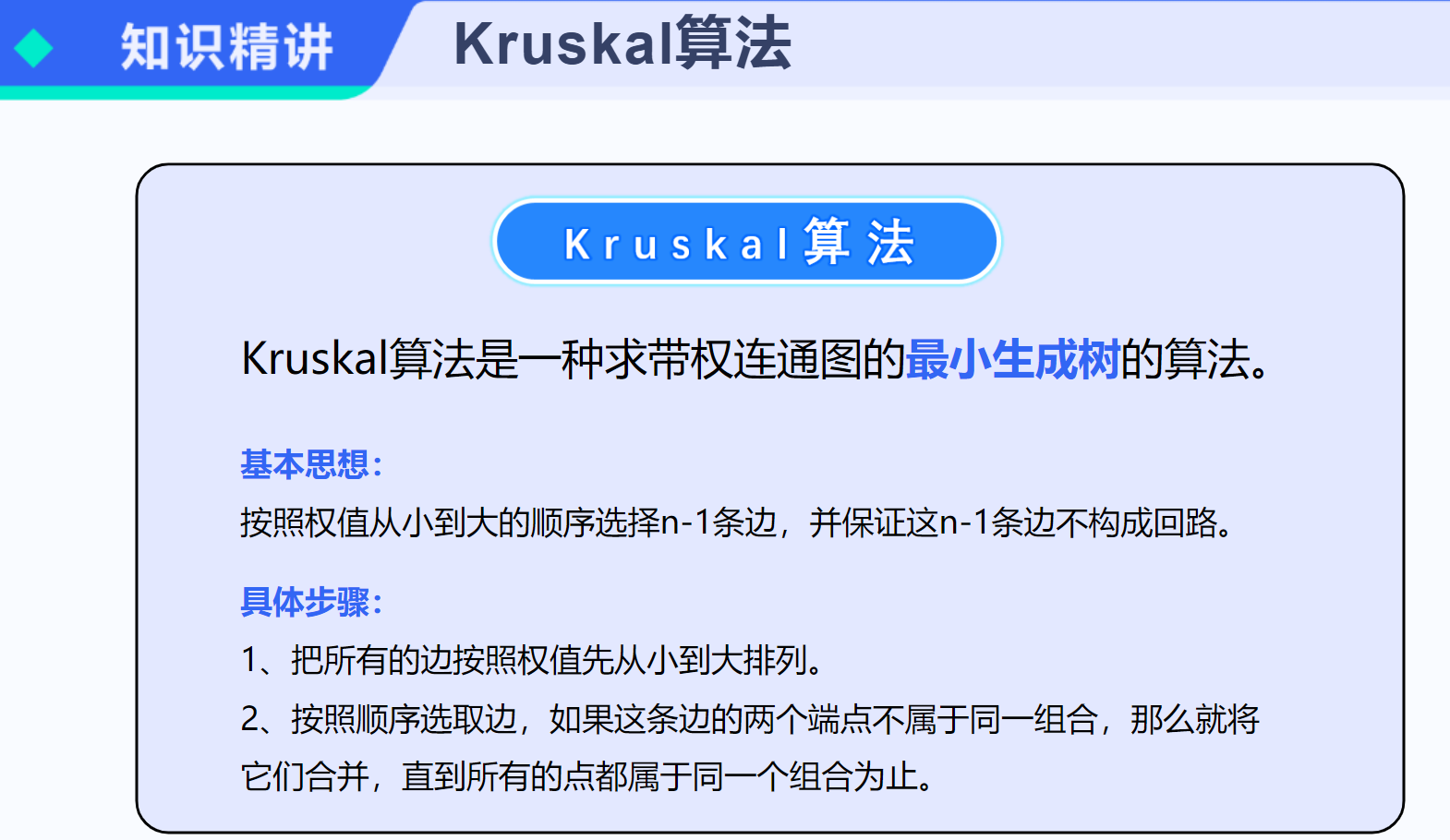
算法步骤 视频：【数据结构——两分钟搞定最小生成树Kruskal算法】 https://www.bilibili.com/video/BV1do4y1v7KZ/?share_source=copy_web&vd_source=d28947bf5669866688dc057b3c41b450
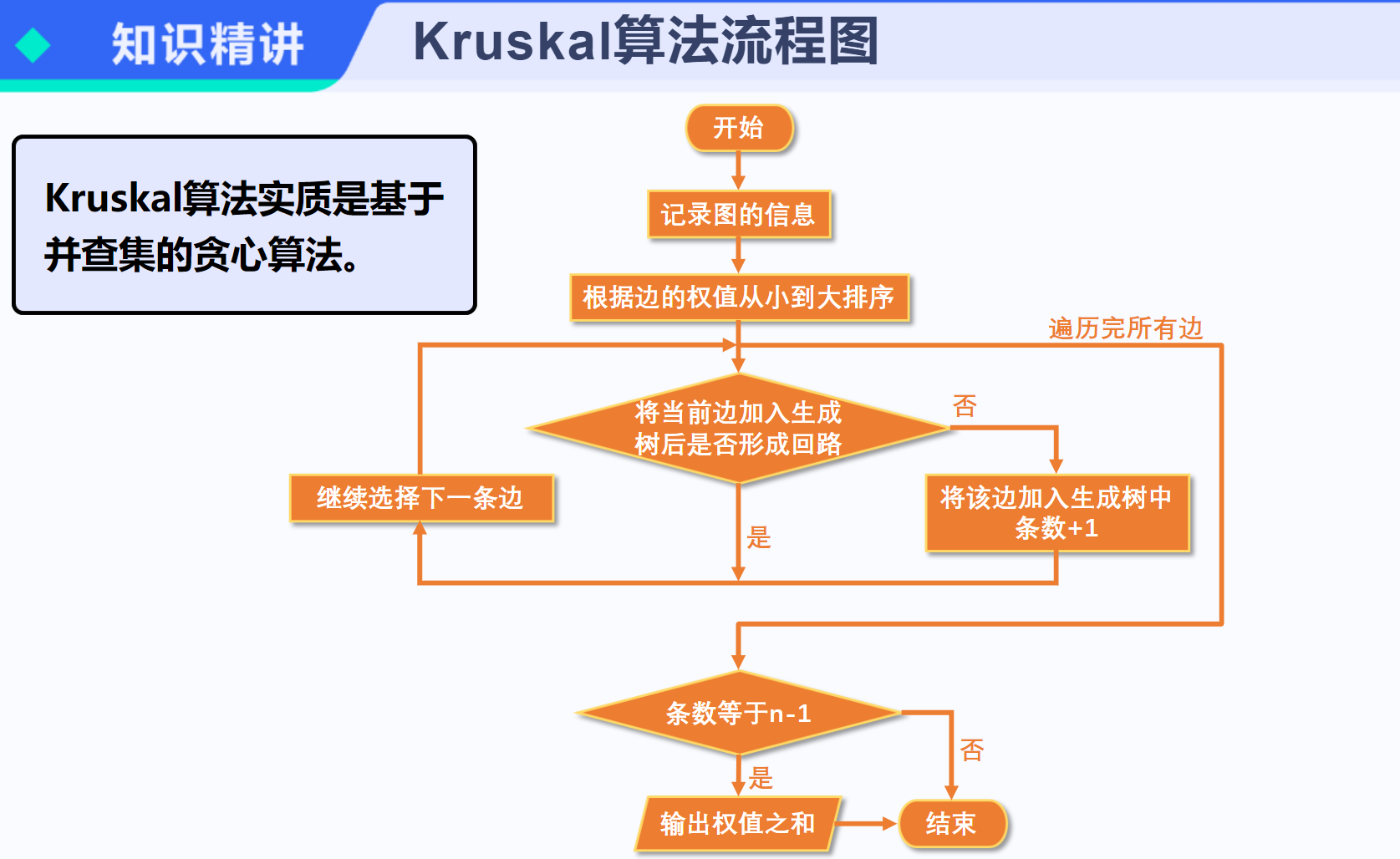
[【最小生成树】最小生成树]
【算法分析】 【kruskal】为了造出一棵最小生成树，我们从最小边权的边开始，按边权从小到大依次加入，如果某次加边产生了环，就扔掉这条边，直到加入了 n−1 条边，即形成了一棵树，判断是否出现环可以使用并查集。 【prim】Prim 算法同样基于上述推论，但思路略有不同。Prim 算法总是维护最小生成树的一部分，即不断向一棵“子最小生成树”中添加节点，直至得到最终结果。最初，Prim 算法仅确定 1 号节点属于最小生成树。 在任意时刻，设已经确定属于最小生成树的部分的节点集合为 T，剩余节点集合为 S。Prim 算法每次找到两个端点分别属于结合 S , T 的权值最小的边 (x,y,z)，然后把点 x 从集合 S 中删除，加入到集合 T，并把 z 累加到答案中。 类比 Dijkstra 算法，我们可以用一个标记数组标记节点是否属于 T。每次从未标记的节点中选出 d 值最小的，把他标记（加入 T ），同时扫描其所有出边，更新另一个端点的 d 值。 【参考代码】 //kruskal #include<bits/stdc++.h> using namespace std; const int maxn = 2e5 + 9; struct node { int x, y, z; }a[maxn]; int fa[5009]; int get(int x) { if (fa[x] == x) return x; return fa[x] = get(fa[x]); } void merge(int x, int y) { fa[get(x)] = get(y); } bool cmp(node A, node B) { return A.z < B.z; } int main() { int n, m; cin >> n >> m; for (int i = 1; i <= n; i++) fa[i] = i; for (int i = 0; i < m; i++) { cin >> a[i].x >> a[i].y >> a[i].z; } sort(a, a + m, cmp); int ans = 0, edge = 0; for (int i = 0; i < m; i++) { if (get(a[i].x) == get(a[i].y)) continue; merge(a[i].x, a[i].y); edge++; ans += a[i].z; } if (edge == n - 1) cout << ans; else cout << "orz"; return 0; } //prim #include<bits/stdc++.h> using namespace std; #define inf 0x3f3f3f3f int a[5009][5009]; int d[5009], vis[5009]; int n, m; bool prim() { memset(d, 0x3f, sizeof(d)); memset(vis, 0, sizeof(vis)); d[1] = 0; for (int i = 1; i <= n; i++) { //每次向集合T中加入一个点 int x = 0; for (int j = 1; j <= n; j++) { //找到离T集合最近的点 if (!vis[j] && d[j] < d[x]) x = j; } if (x == 0) return false; //没有找到点，说明其他点都与T集合不连通 vis[x] = 1; //标记，相当于把点x加入T集合 for (int y = 1; y <= n; y++) { //去更新S集合的点到T集合的距离 if(!vis[y]) d[y] = min(d[y], a[x][y]); } } return true; } int main() { cin >> n >> m; memset(a, 0x3f, sizeof(a)); for (int i = 0; i < m; i++) { int x, y, z; cin >> x >> y >> z; a[x][y] = min(a[x][y], z); a[y][x] = min(a[y][x], z); } if (prim()) { int ans = 0; for (int i = 2; i <= n; i++) ans += d[i]; cout << ans; } else cout << "orz"; return 0; }
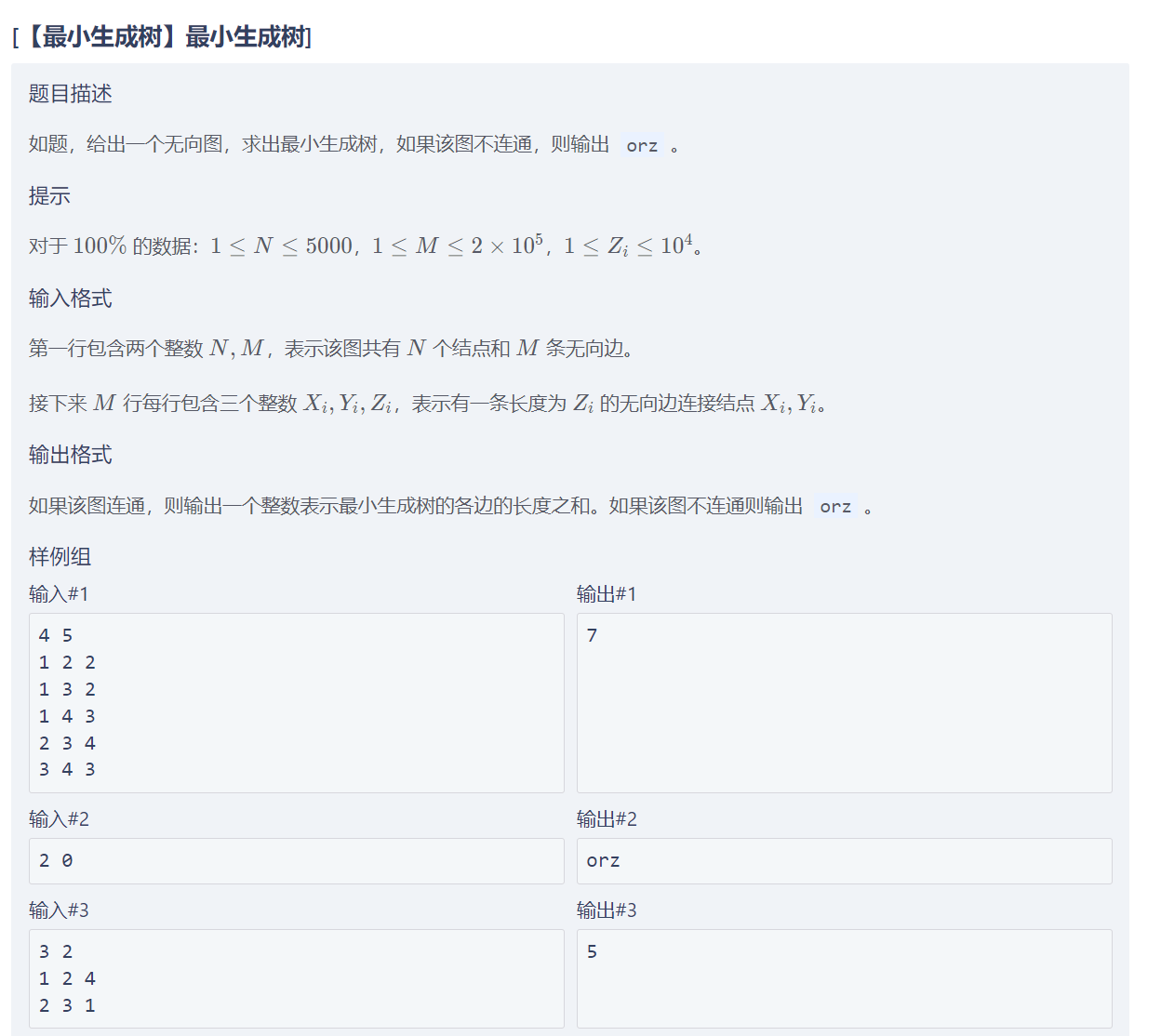
[【最小生成树】畅通工程]
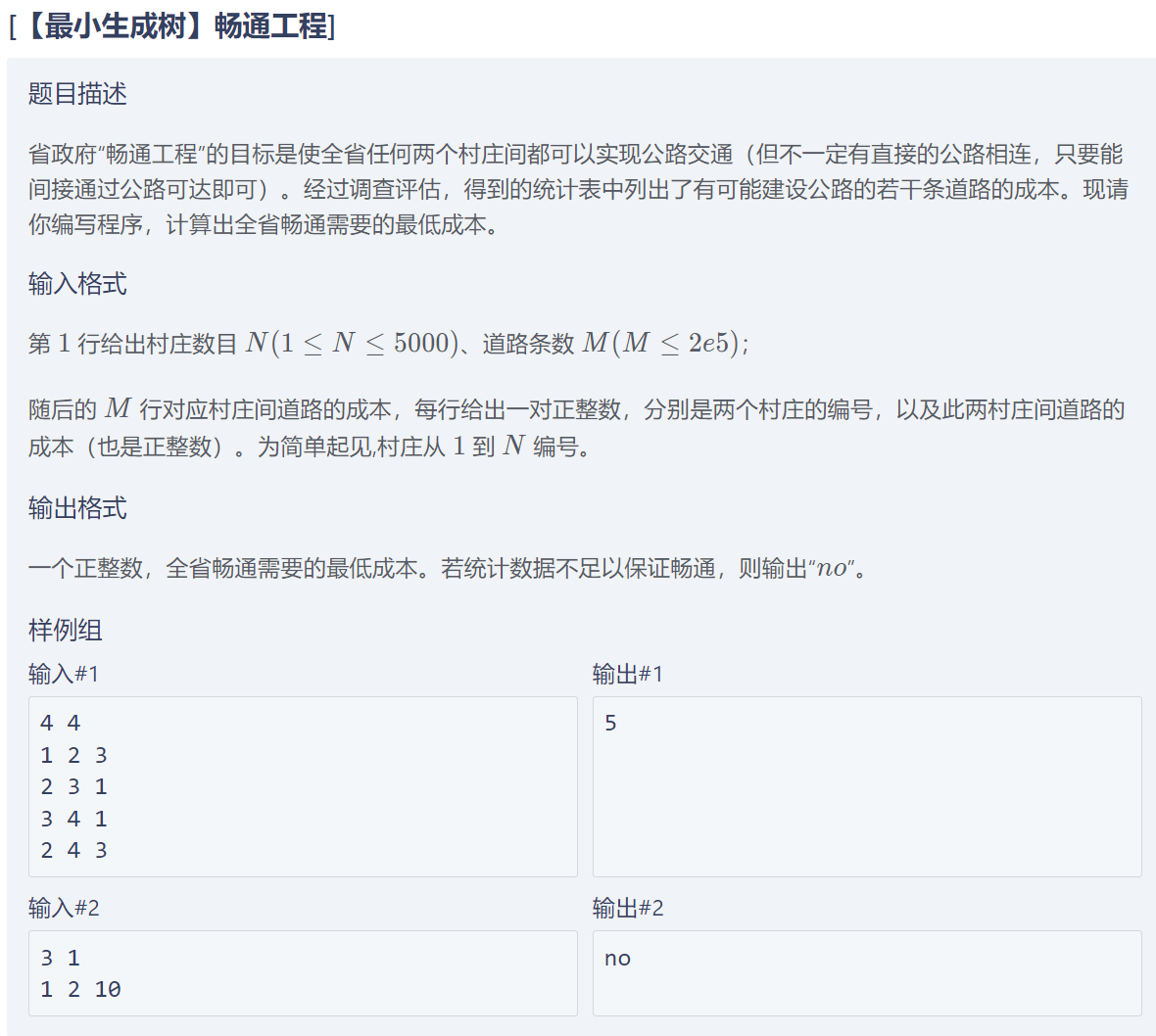
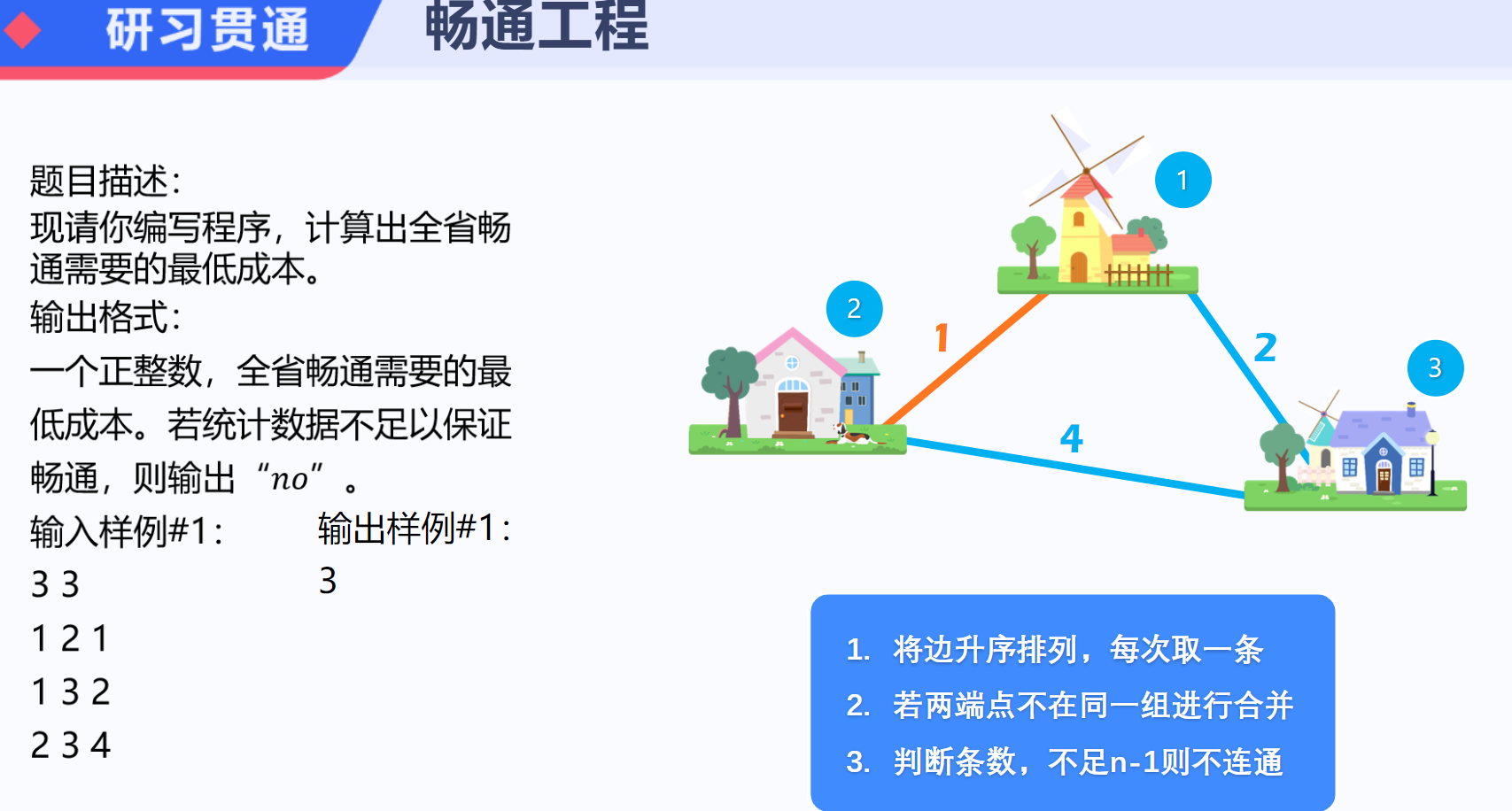
【算法分析】 【kruskal】为了造出一棵最小生成树，我们从最小边权的边开始，按边权从小到大依次加入，如果某次加边产生了环，就扔掉这条边，直到加入了 n−1 条边，即形成了一棵树，判断是否出现环可以使用并查集。 【prim】Prim 算法同样基于上述推论，但思路略有不同。Prim 算法总是维护最小生成树的一部分，即不断向一棵“子最小生成树”中添加节点，直至得到最终结果。最初，Prim 算法仅确定 1 号节点属于最小生成树。 在任意时刻，设已经确定属于最小生成树的部分的节点集合为 T，剩余节点集合为 S。Prim 算法每次找到两个端点分别属于结合 S , T 的权值最小的边 (x,y,z)，然后把点 x 从集合 S 中删除，加入到集合 T，并把 z 累加到答案中。 类比 Dijkstra 算法，我们可以用一个标记数组标记节点是否属于 T。每次从未标记的节点中选出 d 值最小的，把他标记（加入 T ），同时扫描其所有出边，更新另一个端点的 d 值。 【参考代码】 //kruskal #include<bits/stdc++.h> using namespace std; const int maxn = 2e5 + 9; struct node { int x, y, z; }a[maxn]; int fa[5009]; int get(int x) { if (fa[x] == x) return x; return fa[x] = get(fa[x]); } void merge(int x, int y) { fa[get(x)] = get(y); } bool cmp(node A, node B) { return A.z < B.z; } int main() { int n, m; cin >> n >> m; for (int i = 1; i <= n; i++) fa[i] = i; for (int i = 0; i < m; i++) { cin >> a[i].x >> a[i].y >> a[i].z; } sort(a, a + m, cmp); int ans = 0, edge = 0; for (int i = 0; i < m; i++) { if (get(a[i].x) == get(a[i].y)) continue; merge(a[i].x, a[i].y); edge++; ans += a[i].z; } if (edge == n - 1) cout << ans; else cout << "no"; return 0; } //prim #include<bits/stdc++.h> using namespace std; #define inf 0x3f3f3f3f int a[5009][5009]; int d[5009], vis[5009]; int n, m; bool prim() { memset(d, 0x3f, sizeof(d)); memset(vis, 0, sizeof(vis)); d[1] = 0; for (int i = 1; i <= n; i++) { //每次向集合T中加入一个点 int x = 0; for (int j = 1; j <= n; j++) { //找到离T集合最近的点 if (!vis[j] && d[j] < d[x]) x = j; } if (x == 0) return false; //没有找到点，说明其他点都与T集合不连通 vis[x] = 1; //标记，相当于把点x加入T集合 for (int y = 1; y <= n; y++) { //去更新S集合的点到T集合的距离 if(!vis[y]) d[y] = min(d[y], a[x][y]); } } return true; } int main() { cin >> n >> m; memset(a, 0x3f, sizeof(a)); for (int i = 0; i < m; i++) { int x, y, z; cin >> x >> y >> z; a[x][y] = min(a[x][y], z); a[y][x] = min(a[y][x], z); } if (prim()) { int ans = 0; for (int i = 2; i <= n; i++) ans += d[i]; cout << ans; } else cout << "no"; return 0; }
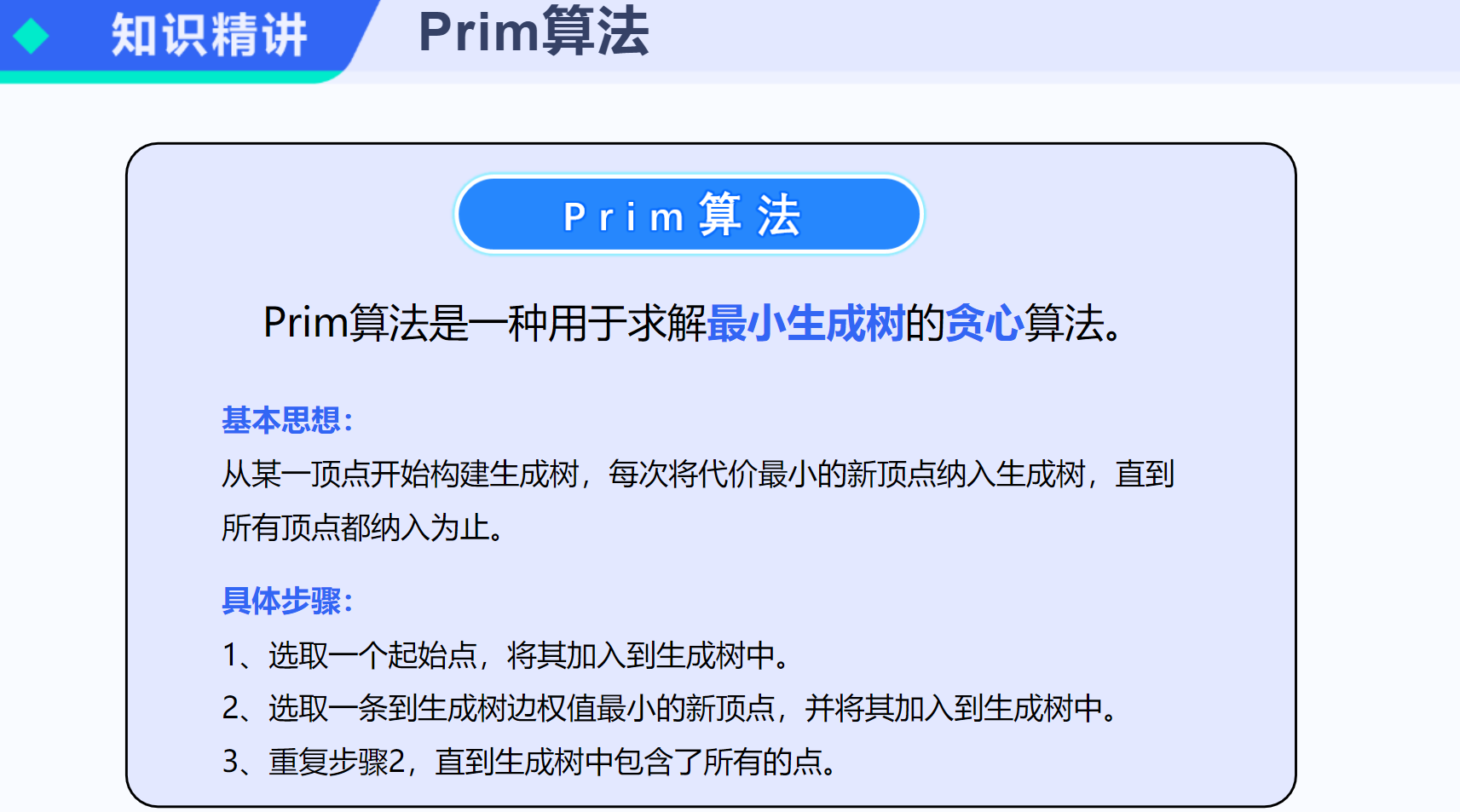
Prim算法是一种在图论中用于在加权连通图中搜索最小生成树的算法。以下是关于Prim算法的详细解释：
定义
Prim算法是一种贪心算法，用于在加权连通图中找到一棵包含所有顶点的最小生成树。这意味着，由该算法搜索到的边子集所构成的树中，不仅包括了连通图里的所有顶点，而且其所有边的权值之和也是最小的。
历史背景
- Prim算法最初由捷克数学家沃伊捷赫·亚尔尼克（Vojtěch Jarník）于1930年发现。
- 随后，在1957年，美国计算机科学家罗伯特·普里姆（Robert C. Prim）独立发现了该算法。
- 由于艾兹格·迪科斯彻（Edsger Dijkstra）在1959年也发现了类似的算法，因此在某些场合，Prim算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。
算法步骤
- 输入：一个加权连通图，其中顶点集合为V，边集合为E。
- 初始化：
- 选择V中的任一节点作为起始点，加入集合U（已访问节点的集合）。
- 初始化一个距离数组dist[]，用于记录从起始点到其他所有节点的最短距离（初始时，除了起始点外，其他节点的距离都设为无穷大）。
- 初始化一个最小边集合MST，开始时为空。
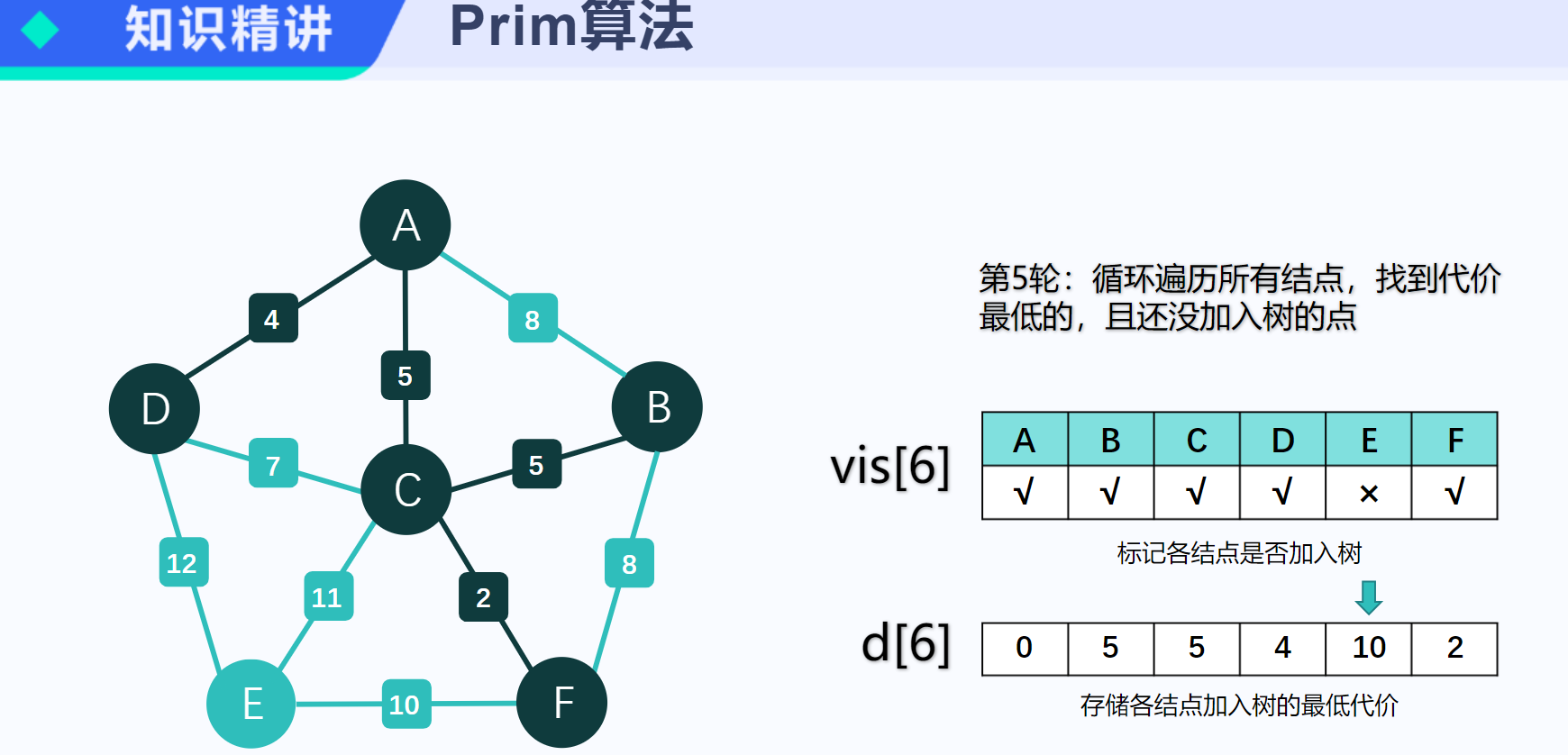
- 重复以下操作，直到U = V：
- 在集合E中选取一条边(u, v)，其中u在U中，v不在U中，且这条边的权值在所有满足条件的边中是最小的。
- 将v加入集合U中，并将边(u, v)加入MST中。
- 更新dist[]数组，考虑通过新加入的节点v，是否可以更新起始点到其他节点的最短距离。
- 输出：使用集合U和MST来描述所得到的最小生成树。
时间复杂度
- 使用邻接矩阵图表示的简易实现中，Prim算法的时间复杂度为O(V^2)，其中V是顶点的数量。
- 使用简单的二叉堆与邻接表来表示的话，Prim算法的运行时间可缩减为O(ElogV)，其中E是边的数量。
- 如果使用较为复杂的斐波那契堆，则可将运行时间进一步缩短为O(E+VlogV)。
应用场景
Prim算法广泛应用于各种需要找到最小成本网络或路径的问题中，例如城市规划、通信网络建设、电路设计等。在这些场景中，通过Prim算法可以找到连接所有点所需的最短总路径或最低成本路径。
算法步骤参考视频：【数据结构——四分钟搞定Prim算法】 https://www.bilibili.com/video/BV1Cv4y1s7kU/?share_source=copy_web&vd_source=d28947bf5669866688dc057b3c41b450
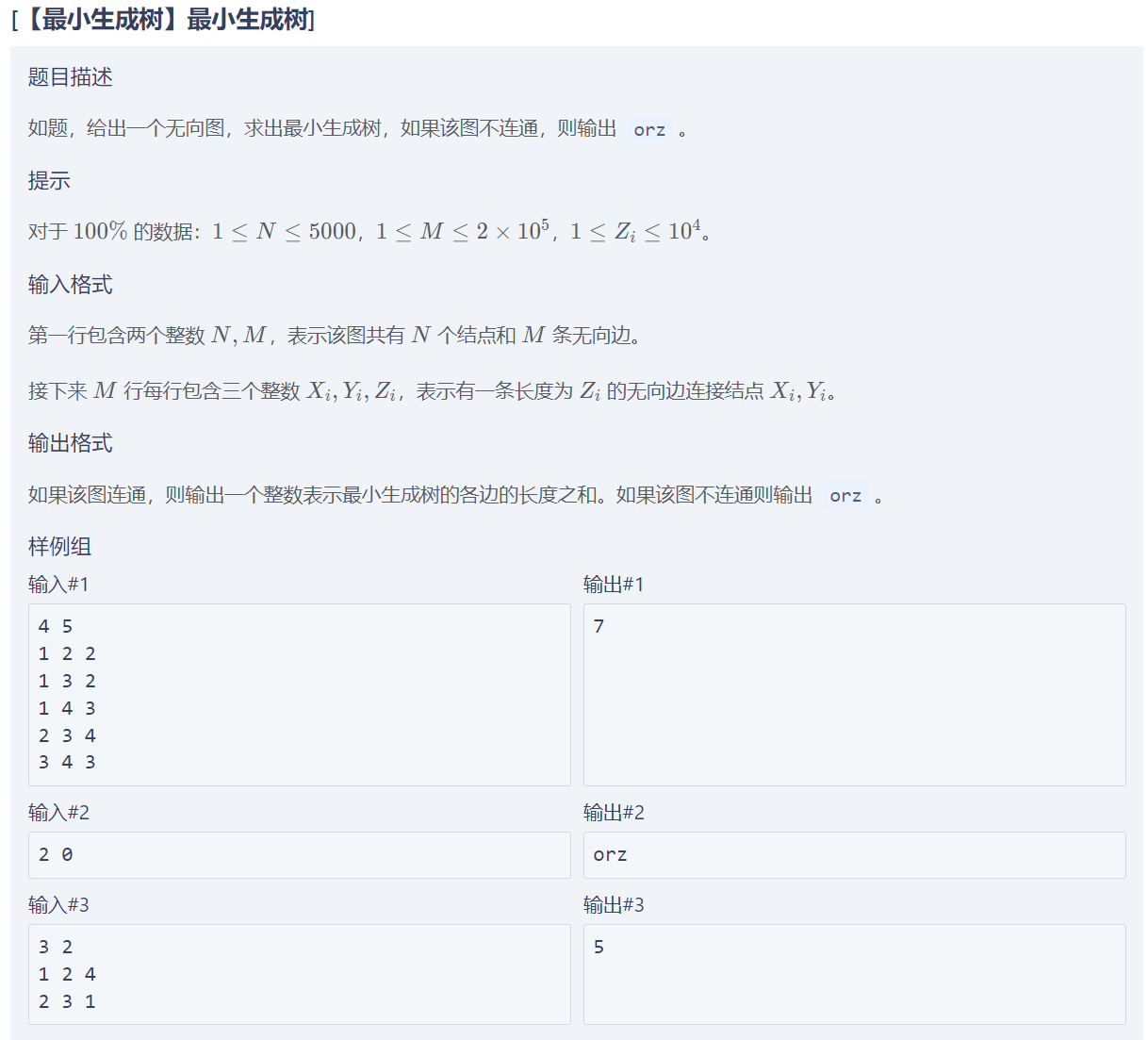
[【最小生成树】最小生成树]
//prim #include<bits/stdc++.h> using namespace std; #define inf 0x3f3f3f3f int a[5009][5009]; int d[5009], vis[5009]; int n, m; bool prim() { memset(d, 0x3f, sizeof(d)); memset(vis, 0, sizeof(vis)); d[1] = 0; for (int i = 1; i <= n; i++) { //每次向集合T中加入一个点 int x = 0; for (int j = 1; j <= n; j++) { //找到离T集合最近的点 if (!vis[j] && d[j] < d[x]) x = j; } if (x == 0) return false; //没有找到点，说明其他点都与T集合不连通 vis[x] = 1; //标记，相当于把点x加入T集合 for (int y = 1; y <= n; y++) { //去更新S集合的点到T集合的距离 if(!vis[y]) d[y] = min(d[y], a[x][y]); } } return true; } int main() { cin >> n >> m; memset(a, 0x3f, sizeof(a)); for (int i = 0; i < m; i++) { int x, y, z; cin >> x >> y >> z; a[x][y] = min(a[x][y], z); a[y][x] = min(a[y][x], z); } if (prim()) { int ans = 0; for (int i = 2; i <= n; i++) ans += d[i]; cout << ans; } else cout << "orz"; return 0; }
