python 中matplotlib画图笔记

图形样式

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

# x范围
x = np.linspace(-np.pi, np.pi, 200)
# 定义正弦、余弦函数
c, s = np.cos(x), np.sin(x)

# 画出正、余弦函数，设置好线的颜色、线宽、线型号
plt.plot(x, c, color='blue', linewidth=2.0, linestyle='-', label='cos')
plt.plot(x, s, color='red', linewidth=2.0, linestyle='-', label='sin')

"""画出当x=2π/3 与 正余弦的交线(虚线)"""

# 设置坐标轴的长度范围: x,y的最大最小值*1.1，多显示一点范围
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)

# 设置坐标轴的刻度
plt.xticks((-np.pi, -np.pi/2, np.pi/2, np.pi), 
          (r'$\pi$', r'$-\frac{\pi}{2}$', r'$\frac{\pi}{2}$', r'$\pi$'))  # 使用LaTeX格式显示π

plt.yticks([-1, -0.5, 0, 0.5, 1])

ax = plt.gca()  # gca代表当前坐标轴：get current axis
ax.spines['right'].set_color('none')  # 隐藏右边、和上边的坐标轴
ax.spines['top'].set_color('none')

ax.xaxis.set_ticks_position('bottom')  # 设置x轴刻度显示位置
ax.spines['bottom'].set_position(('data', 0))  # 将下边的坐标轴设置到原点0的位置

ax.yaxis.set_ticks_position('left')  # 设置y轴刻度显示位置
ax.spines['left'].set_position(('data', 0))  # 将y轴坐标原点设置到0

# 图片左上角添加图例，用于识别正余弦
plt.legend(loc='upper left')

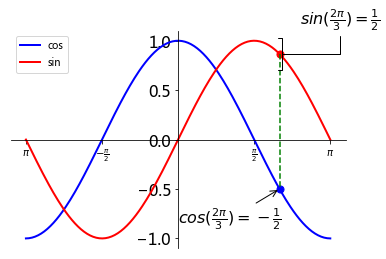
# 画出 x= 2π/3处与正余弦相交的线
t = 2 * np.pi / 3
plt.plot([t, t], [np.sin(t), np.cos(t)], color='green', linewidth=1.5, linestyle='--')

# 画出两个交点
plt.scatter([t, ], [np.cos(t), ], 50, color='blue')
plt.scatter([t, ], [np.sin(t), ], 50, color='red')

# 画出两个点的标注 
plt.annotate(r'$cos(\frac{2\pi}{3})=-\frac{1}{2}$',  # cos(x)交点标注文本内容
            xy=(t, np.cos(t)),  # 被注释的坐标点的位置
            xycoords='data',  # 被注释点的坐标属性,data表示以xy为参考，其他值表示以原点等为参考
            ha='center',  # 点在注释的中心，水平方向。默认是文本左下角
            va='center',  # 垂直
            xytext=(-50, -30),  # 标注文本相对箭头的坐标位置
            textcoords='offset points',  # 相当于被注释点偏移量，单位是点
            fontsize=16,  # 标注文本的字体大小
            arrowprops=dict(arrowstyle='->',  # 箭头属性
                           connectionstyle='arc3'))  # 连接方式

plt.annotate(r'$sin(\frac{2\pi}{3})=\frac{1}{2}$',
            xy=(t, np.sin(t)),
            xycoords='data',
            xytext=(20, 30),
            textcoords='offset pixels',  # 相当于被注释点偏移量，单位是像素
            fontsize=16,
            arrowprops=dict(arrowstyle='-[',  # 箭头属性
                           connectionstyle='angle'))  # 连接方式：直角

for label in ax.get_yticklabels():
    label.set_fontsize(16)
    label.set_bbox(dict(facecolor='white', edgecolor='None', alpha=0.65))

图形对象

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-np.pi, np.pi, 200, endpoint=True)
c, s = np.cos(x), np.sin(x)

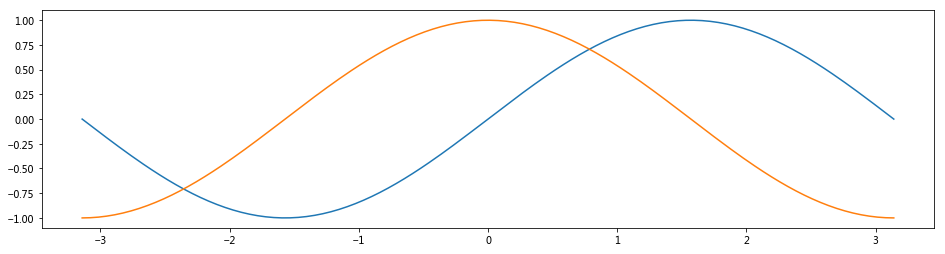
# 创建sin图像窗口
plt.figure(num='sin', figsize=(16, 4))
# 画图
plt.plot(x, s)

# 创建cos图像窗口
plt.figure(num='cos', figsize=(16, 4))
plt.plot(x, c)

# 选择sin窗口
plt.figure(num='sin')
# 在上面画图
plt.plot(x, c)

# 输出量窗口的编号
print(plt.figure(num='sin').number)
print(plt.figure(num='cos').number)

分区域作图

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

plt.figure(figsize=(18, 4))

plt.subplot(2, 2, 1)
plt.xticks(())  # x,y轴不显示刻度
plt.yticks(())
# plt.axis('off') 不显示坐标轴（4个边框边界）
# 分别为文本显示的：x、y坐标，文本内容，中心点，文本大小，透明度
plt.text(0.5, 0.5, 'subplot(2, 2, 1)', ha='center', va='center',
        size=20, alpha=.5)

plt.subplot(2, 2, 2)
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'subplot(2, 2, 2)', ha='center', va='center',
        size=20, alpha=.5)

plt.subplot(2, 2, 3)
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'subplot(2, 2, 3)', ha='center', va='center',
        size=20, alpha=.5)

plt.subplot(2, 2, 4)
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'subplot(2, 2, 4)', ha='center', va='center',
        size=20, alpha=.5)

# 自动调整子图参数，使之填充整个图像区域。有时候可能不工作
# 仅仅检查坐标轴标签、刻度标签以及标题的部分
plt.tight_layout()

更复杂的子图布局

用gridspec来实现

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# 先导入模块
import matplotlib.gridspec as gridspec

plt.figure(figsize=(18, 4))
# 创建图像窗口
G = gridspec.GridSpec(3, 3)

axes_1 = plt.subplot(G[0, :])  # 占用第一行、所有的列
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'Axes 1', ha='center', va='center',
        size=24, alpha=.5)

axes_2 = plt.subplot(G[1:, 0])  # 占用第二行开始的所有行，的第1列
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'Axes 2', ha='center', va='center',
        size=24, alpha=.5)

axes_3= plt.subplot(G[1:, -1])  # 占用第二行开始的所有行，的最后1列
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'Axes 3', ha='center', va='center',
        size=24, alpha=.5)

axes_4 = plt.subplot(G[1, -2])  # 占用第二行，倒数第2列
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'Axes 4', ha='center', va='center',
        size=24, alpha=.5)

axes_5 = plt.subplot(G[-1, -2])  # 占用最后1行，倒数第2列
# plt.xticks(())
# plt.yticks(())
plt.text(0.5, 0.5, 'Axes 5', ha='center', va='center',
        size=24, alpha=.5)

plt.tight_layout()

创建坐标轴

plt.axes()

%matplotlib inline
import matplotlib.pyplot as plt

plt.figure(figsize=(18, 4))

# [left, botom, width, height]
plt.axes([.1, .1, .8, .8])
plt.xticks(())
plt.yticks(())
plt.text(.2, .5, 'axes([0.1, 0.1, 0.8, 0.8])', ha='center', va='center',
        size=20, alpha=.5)

plt.axes([.5, .5, .3, .3])
plt.xticks(())
plt.yticks(())
plt.text(.2, .5, 'axes([.5, .5, .3, .3])', ha='center', va='center',
        size=16, alpha=.5)

Text(0.2, 0.5, 'axes([.5, .5, .3, .3])')

坐标刻度

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

# 定义 画坐标轴的函数，返回坐标轴
def tickline():
    plt.xlim(0, 10)  # 设置xy轴范围
    plt.ylim(-1, 1)
    plt.yticks([])  # 不显示y坐标刻度
    
    # gca表示选择当前坐标轴
    ax = plt.gca()
    ax.spines['right'].set_color('none')  # 设置其他三个坐标轴边框不显示
    ax.spines['left'].set_color('none')
    ax.spines['top'].set_color('none')
    
    ax.xaxis.set_ticks_position('bottom')  # x轴刻度显示 位置
    ax.spines['bottom'].set_position(('data', 0))  # 将x轴坐标原点设置到0
    
    ax.yaxis.set_ticks_position('none')  # y轴刻度 不显示（此代码可以省略）
    
    # 显示坐标轴刻度，步长为0.1
    ax.xaxis.set_minor_locator(plt.MultipleLocator(0.1))
    
    # 遍历x，y轴的标签，更改标签的 字体大小
    for label in ax.get_xticklabels() + ax.get_yticklabels():
        label.set_fontsize(16)
    
    # 画出ax的图，设定x，y的数据集
    ax.plot(np.arange(11), np.zeros(11))
    return ax

# 定义标签选项，便于后续遍历提取内容
locators =[
    'plt.NullLocator()',  # 不显示坐标标签， 只显示坐标刻度
    'plt.MultipleLocator(base=1.0)',  # 以固定的步长，显示多个坐标标签
    'plt.FixedLocator(locs=[0, 2, 8, 9, 10])',  # 以列表形式，显示固定的坐标标签
    'plt.IndexLocator(base=3, offset=1)',  # 以offset为起点位置，每隔base步长，就画一个坐标标签
    'plt.LinearLocator(numticks=5)',  # 把坐标轴的长度均分为numticks个数，显示坐标标签
    'plt.LogLocator(base=2, subs=[1.0])',  # 以对数为步长显示标签
    'plt.MaxNLocator(nbins=3, steps=[1, 3, 5, 7, 9, 10])',  # 从提供的标签列表里，显示出最大不超过nbins个数的标签
    'plt.AutoLocator()'  # 自动显示标签
]
n_locators = len(locators)

# 定义size，元组形式
size = 1024, 60 * n_locators
dpi = 72.0
# 除以像素，得到图像窗口大小
figsize = size[0] / float(dpi), size[1] / float(dpi)

# 定义图像窗口
fig = plt.figure(figsize=figsize, dpi=dpi)
# 设置图形的透明度
fig.patch.set_alpha(0)

# 遍历
for i, locator in enumerate(locators):
    # 定义图像窗口，从1开始，所以i要+1
    plt.subplot(n_locators, 1, i+1)
    # 画出对应坐标轴，并返回坐标轴对象ax
    ax = tickline()
    # 设置坐标轴的label显示方式；eval()执行括号里面字符串的返回结果，类似于计算器
    ax.xaxis.set_major_locator(eval(locator))
    # 在此坐标轴上写出文字
    plt.text(5, 0.3, locator[3:], ha='center', va='center', size=16)

# 调整图形周边空间的大小
fig.subplots_adjust(bottom=.01, top=.99, left=.01, right=.99)

画点与填充

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import random

散点图

n = 1024
# 生成1024个随机的数，范围在0-1之间
x = np.random.normal(0, 1, n)
# x和y不一定相等
y = np.random.normal(0, 1, n)

# 反正切函数
t = np.arctan2(y, x)

plt.subplot(1, 2, 1)
plt.scatter(x, y, s=75, c=t, alpha=.5)

plt.xlim(-1.5, 1,5)
plt.xticks(())

plt.ylim(-1.5, 1.5)
plt.yticks(())

填充图

plt.fill_between()

n = 256
x = np.linspace(-np.pi, np.pi, n, endpoint=True)
y = np.sin(2 * x)

plt.subplot(1, 2, 2)
# 画出正弦图像，图像y+1，上移1个单位
plt.plot(x, y + 1, color='blue', alpha=1.00)
# 填充：y+1的值，和1之间的区域
plt.fill_between(x, 1, y + 1, color='blue', alpha=0.25)

<matplotlib.collections.PolyCollection at 0x7fbc3aabb0f0>

plt.plot(x, y - 1, color='blue', alpha=1.00)
# 可以采用判断语句，结果为bool型，0或1
plt.fill_between(x, -1, (y - 1) > -1, color='blue', alpha=.25)
plt.fill_between(x, -1, (y - 1) < -1, color='red', alpha=.25)

plt.xlim(-np.pi, np.pi)
# plt.xticks(())
plt.ylim(-2.5, 2.5)
# plt.yticks(())

(-2.5, 2.5)

柱状图

plt.bar()

n = 12
x = np.arange(n)
# 设置函数
y1 = (1 - x / float(n)) * np.random.uniform(0.5, 1.0, n)
y2 = (1 - x / float(n)) * np.random.uniform(0.5, 1.0, n)

# 定义窗口大小
plt.figure(figsize=(18, 10))
plt.subplot(1, 2, 1)

# 柱形图
plt.bar(x, +y1, facecolor='#9999ff', edgecolor='black') # edgecolor边框颜色
plt.bar(x, -y2, facecolor='#ff9999', edgecolor='white')

# 每个柱状图添加文字
# zip：将x，y数据组合起来，再画图
for m, n in zip(x, y1):
    plt.text(m, n + 0.02, '%.2f' % n, ha='center', va='bottom')
    
for m, n in zip(x, -y2):
    plt.text(m, n - 0.05, '%.2f' % n, ha='center', va='bottom')
    

网格图

plt.grid()

import numpy as np
import matplotlib.pyplot as plt

数据类型一：点与点之间不连线

# x，y的值
x = np.array([0, 1, 2, 0, 1, 2])
y = np.array([0, 0, 0, 1, 1, 1])


plt.plot(x, y,
         color='red',  # 全部点设置为红色
         marker='.',  # 点的形状为圆点
         linestyle='')  # 线型为空，也即点与点之间不用线连接
plt.grid(True)
plt.show()

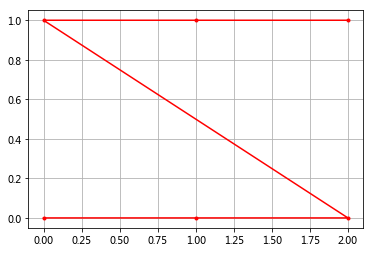
数据类型一：点与点之间连线

# x，y的值
x = np.array([0, 1, 2, 0, 1, 2])
y = np.array([0, 0, 0, 1, 1, 1])


plt.plot(x, y,
         color='red',  # 全部点设置为红色
         marker='.',  # 点的形状为圆点
         linestyle='-')  # 线型（画出的线会根据画点的顺序依次连接）
plt.grid(True)
plt.show()

数据类型二：点与点之间连线（纵向）

x = np.array([[0, 1, 2], 
              [0, 1, 2], 
              [0, 1, 2], 
              [0, 1, 2]])

y = np.array([[0, 0, 0], 
              [1, 1, 1], 
              [2, 2, 2], 
              [3, 3, 3]])

plt.plot(x, y,
         color='red',  # 全部点设置为红色
         marker='.',  # 点的形状为圆点
         markersize=10,  # 设置点大小
         linestyle='-.')  # 设置线型，matplot中会把每一列的点连成一条线
plt.grid(True)
plt.show()

如果网格比较多，用上述方法就比较笨，

所以需要用numpy.meshgrid()函数

import numpy as np
import matplotlib.pyplot as plt

x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 2, 4, 6])

"""
# 使用函数，将x,y生成上述方法中的矩阵
# 相当于将x中的每个元素，要映射到y中的每个元素，所有元素两两组合形成的坐标，不是一一对应关系

# 生成网格数据，1个x对应所有的y
# 将 x一行的数据，重复y行
# 将 y的每个元素重复x次，生成y行
# 生成后的数据，实现一一对应功能。
"""
X, Y = np.meshgrid(x, y)
print(X)
print(Y)

plt.plot(X, Y,
         color='red',  # 全部点设置为红色
         marker='.',  # 点的形状为圆点
         linestyle='')  # 线型为空，也即点与点之间不用线连接
plt.grid(True)
plt.show()

[[0 1 2 3 4]
 [0 1 2 3 4]
 [0 1 2 3 4]
 [0 1 2 3 4]]
[[0 0 0 0 0]
 [2 2 2 2 2]
 [4 4 4 4 4]
 [6 6 6 6 6]]

plt.figure(figsize=(15, 9))
# 生成0-1000之间，20个平均分布的点
x = np.linspace(0,1000,20)
y = np.linspace(0,500,20)

X,Y = np.meshgrid(x, y)

plt.plot(X, Y,
         color='limegreen',  # 设置颜色为limegreen
         marker='.',  # 设置点类型为圆点
         linestyle='')  # 设置线型为空，也即没有线连接点
plt.grid(True)
plt.show()

网格图2

plt.figure(figsize=(18, 9))
# 创建窗口
ax = plt.subplot(1, 2, 1)

ax.set_xlim(0, 4)
ax.set_ylim(0, 3)

"""刻度"""
# x轴每间隔1个单位，取一个值：major
ax.xaxis.set_major_locator(plt.MultipleLocator(1.0))
# x轴最小刻度单位为0.1:minor
ax.xaxis.set_minor_locator(plt.MultipleLocator(0.1))
# y轴
ax.yaxis.set_major_locator(plt.MultipleLocator(1.0))
ax.yaxis.set_minor_locator(plt.MultipleLocator(0.1))

"""表格线"""
# 设置线宽等参数
ax.grid(which='major', axis='x', linewidth='1', linestyle='-.', color='0.1')
ax.grid(which='minor', axis='x', linewidth='0.25', linestyle='-', color='0.75')
ax.grid(which='major', axis='y', linewidth='1', linestyle='-.', color='0.1')
ax.grid(which='minor', axis='y', linewidth='0.25', linestyle='-', color='0.75')

ax.set_xticklabels(())
ax.set_yticklabels(())

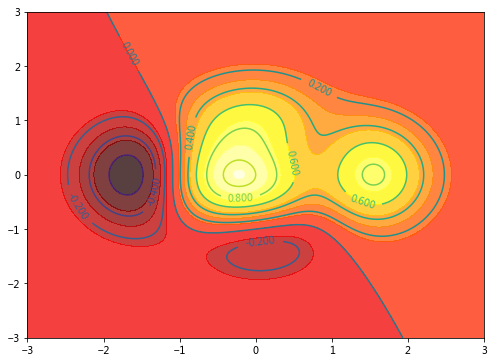
等高线图

plt.contour()

# 定义等高线的方程：类似于圆的方程
def f(x, y):
    return(1 - x / 2 + x**5 + y**3) * np.exp(-x**2 - y**2)
    # return (x ** 2 + y**2)
    # return x +y
    
n = 256
# 生成256个-3到3之间的点
x = np.linspace(-3, 3, n)
y = np.linspace(-3, 3, n)

# 生成网格数据，1个x对应所有的y
# 将 x一行的数据，重复y行
# 将 y的每个元素重复x次，生成y行
# 生成后的数据，实现一一对应功能。
x, y = np.meshgrid(x, y)
# print(x)
# print(y)

plt.figure(figsize=(18, 6))
plt.subplot(1, 2, 2)

# 热点图 背景：背景根据数值不同，分成多个层次，以不同颜色显示
# 数字15代表层级，数字越大，层数越多
plt.contourf(x, y, f(x, y), 15, alpha=.75, cmap=plt.cm.hot)

# 等高线： 根据数值不同，画出不同的等高线
c = plt.contour(x, y, f(x, y), 10)

# 显示等高线 上面的标注文字
plt.clabel(c, inline=1, fontsize=10)

# plt.xticks(())
# plt.yticks(())

热成像图

plt.imshow()

plt.figure(figsize=(18, 10))
def f(x, y):
    return(1 - x / 2 + x**5 + y**3) * np.exp(-x**2 - y**2)
#     return x+y
plt.subplot(1, 2, 1)
n = 10

x = np.linspace(-3, 3, 4*n)
y = np.linspace(-3, 3, 3*n)
m, n = np.meshgrid(x, y)

# 画热成像图
plt.imshow(f(m, n), cmap='hot', origin='low')
# 颜色条
plt.colorbar(shrink=0.43)

plt.xticks(())
plt.yticks(())

饼图

plt.pie()

plt.figure(figsize=(18, 18))
plt.subplot(1, 2, 2)
n = 20
# 定义变量，表示饼图中饼的个数
z = np.ones(n)
z[-1] *= 2 # 面积和其他19个 不一样，是其他单个扇形的2倍

# explode表示中心圆的半径
# 不同部分，颜色不一样
plt.pie(z, explode=z*0.2, colors=['%f' % (i/float(n)*1000) for i in range(n)] )
plt.axis('equal')

# plt.xticks(())
# plt.yticks(())

(-1.3291114604228391,
 1.5113406046531497,
 -1.3204101114481226,
 1.3204101082372062)

极坐标图

plt.figure(figsize=(18, 18))
# 创建极坐标 窗口
# 一定要加上polar=True，不然就是条形图
ax = plt.subplot(1, 2, 2, polar=True)

n = 20
# 0-2π之间，步长为2π/n
theta = np.arange(0.0, 2*np.pi, 2*np.pi/n)

# 生成20个随机数
radii = 10 * np.random.rand(n)
# 扇形宽度？
width = np.pi / 4 * np.random.rand(n)

# 画图极坐标图
bars = plt.bar(theta, radii, width=width, bottom=0.0)

for r, bar in zip(radii, bars):
    # 填充不同的颜色
    bar.set_facecolor(plt.cm.jet(r/10))
    bar.set_alpha(0.5)

ax.set_xticklabels([])
ax.set_yticklabels([])

参考自：《scikit-learn机器学习：常用算法原理及编程实战》黄永昌