《Three.js 入门指南》3.1.1 - 基本几何形状 -圆环结(TorusKnotGeometry)
3.1 基本几何形状
圆环结(TorusKnotGeometry)
构造函数
THREE.TorusKnotGeometry(radius, tube, radialSegments, tubularSegments, p, q, heightScale)
圆环节和圆环很相似,只是多了一些参数。
radius : 圆环的半径,默认值为1。
tube : 管道的半径,默认值为0.4。
tubularSegments : 管道的分段数量,默认值为64。
radialSegments : 横截面分段数量,默认值为8。
p : 这个值决定了几何体将绕着其旋转对称轴旋转多少次,默认值是2。
q : 这个值决定了几何体将绕着其内部圆环旋转多少次,默认值是3。
一个标准圆环结的示例demo以及效果
</html>
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<meta http-equiv="X-UA-Compatible" content="ie=edge">
<script type="text/javascript" src="./three.js"></script>
<script type="text/javascript" src="./OrbitControls.js"></script>
<title>Document</title>
</head>
<body>
<script>
init();
function init() {
var renderer = new THREE.WebGLRenderer();
renderer.setSize(800, 600);
document.getElementsByTagName('body')[0].appendChild(renderer.domElement);
renderer.setClearColor(0x000000);
var scene = new THREE.Scene();
var aspect = window.innerWidth / window.innerHeight;
var camera = new THREE.OrthographicCamera(-4 * aspect, 4 * aspect, -3 * aspect, 3 * aspect, 1, 10000);
camera.position.set(50, 50, 500);
camera.lookAt(new THREE.Vector3(0, 0, 0));
scene.add(camera);
var torus = new THREE.Mesh(new THREE.TorusKnotGeometry(3, 0.4, 200, 10, 2, 3),
new THREE.MeshBasicMaterial({
color: 0xff0000,
wireframe: true
})
)
scene.add(torus);
renderer.render(scene, camera);
}
</script>
</body>
</html>

关于圆环结的参数的一些演示说明
radius : 圆环的半径,默认值为1。
tube : 管道的半径,默认值为0.4。
tubularSegments : 管道的分段数量,默认值为64。
radialSegments : 横截面分段数量,默认值为8。
p : 这个值决定了几何体将绕着其旋转对称轴旋转多少次,默认值是2。
q : 这个值决定了几何体将绕着其内部圆环旋转多少次,默认值是3。
这六个值是我们在绘制一个圆环结的时候一般需要设定的参数,radius控制了整个图形的大小。tube设定了圆环的粗细。
对于两个Segments分段切片值,在数值较小的时候,这个radialSegments值,一般被用来实现特殊的效果。例如如果是3,那么就是一个三个面的环带,还可以是四面,n面,也就是截断的横截面的平面形状,而tubelarSegments值,可以实现不一定是圆环。
在数值较大的时候,通常是在控制图形的精细度。
我们需要说明的是p、q这两个值。
对于p值,我们可以想象水管的收纳方式。

对于q值,我们可以想象成把一个儿童塑料弹簧玩具首尾相接:

我们借由这种抽象辅助理解:
p : 这个值决定了几何体将绕着其旋转对称轴旋转多少次,默认值是2。
q : 这个值决定了几何体将绕着其内部圆环旋转多少次,默认值是3。
官方文档的demo床:
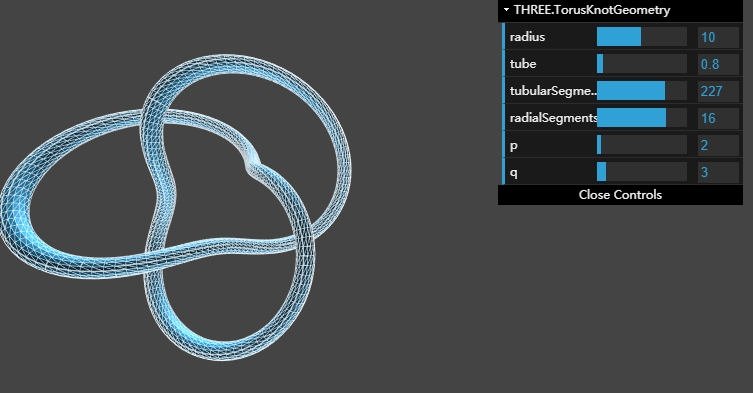

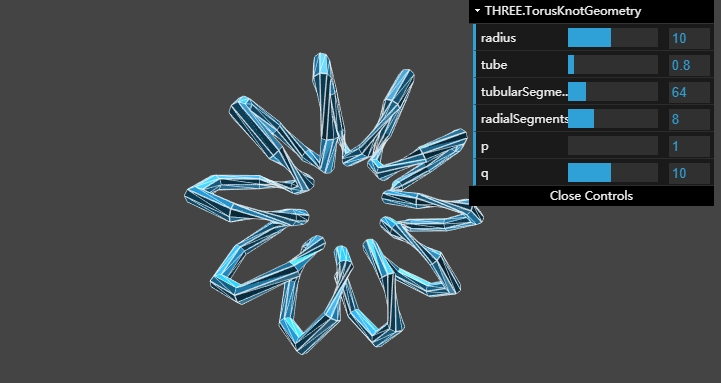
这两个参数相当复杂,通过不同的搭配组合,奇偶数、比例等多种规律可以构建出无数种神奇的图形。更多的示例,通过该图床可以进行演示创造:
https://threejs.org/docs/index.html#api/zh/geometries/TorusKnotGeometry


 浙公网安备 33010602011771号
浙公网安备 33010602011771号