如何用齿轮法测定光速

　　之前在看《从一到无穷大：科学中的事实和胰测》（乔治·伽莫夫著）这本书的时候，其中有个章节是讲时间和空间关系的，里面讲到对于光速的测定。下面是原书中人们对于如何测定光速的描述：

　　第一次测定光速的尝试是著名的意大利物理学家伽利略（Galileo Galilei）在 17 世纪进行的。他和他的助手在一个黑沉沉的夜晚到了佛罗伦萨郊外的旷野，随身带着两盏有遮光板的灯，彼此离开几英里站定。伽利略在某个时刻打开遮光板，让一束光向助手的方向射去。助手已得到指示，一见到从伽利略那里射来的光，就马上打开自己那块遮光板。既然光线从伽利略那里到达助手，再从助手那里折回来都需要一定时间，那么，从伽利略打开遮光板时起，到看到助手发回的光线，也应有一个时间间隔。实际上，他也确实观察到一个小间隔，但是，当伽利略让助手站到远一倍的地方再做这个实验时,间隔却没有增大。显然，光线走得太快了，走几英里路简直用不了多少时间。至于观察到的那个间隔，事实上是由于伽利略的助手没能在见到光线时立即打开遮光板造成的——这在今天称为反应迟误。

　　很显然，在今天看来，伽利略的这种方式是无法测量光速的，事实上由于光速特别快，靠常规的测量距离和人的反应速度来记录时间是不可能的。那还有别的方式来测量光速吗？答案是肯定的，毕竟，我们现在都知道，光速被定义为一个常量，一般来说，传播速度为30万千米每秒。

　　在这本书上有介绍，下面是原文中的描述：

　　不过，用伽利略这套粗糙的遮光灯所做不到的，后来用更精密的物理仪器做到了。我们看到的是法国物理学家斐佐（Fizeau）首先采用的短距离测定光速的设备。它的主要部件是安在同一根轴上的两个齿轮，两个齿轮的安装正好使我们在沿轴的方向从一头看去时，第一个齿轮的齿对着第二个齿轮的齿缝。这样，一束很细的光沿平行于轴的方向射出时，无论这套齿轮处在那个位置上，都不能穿过这套齿轮。现在让这套齿轮系统以高速转动。从第一个齿轮的齿缝射入的光线，总是需要一些时间才能达到第二个齿轮。如果在这段时间内，这套齿轮系统恰好转过半个齿，那么，这束光线就能通过第二个齿轮了。这种情况与汽车以适当速度沿装有定时红绿灯系统的街道行驶的情况很类似。如果这套齿轮的转速提高一倍，那么，光线在到达第二个齿轮时，正好射到转来的齿上,光线就又被挡住了。但转速再提高时，这个齿又将在光束到达之前转过去，相邻的齿缝恰好在这适当的时刻转来让光线射过去。因此，注意光线出现和消失（或从消失到出现）所相应的转速，就能算出光线在两齿轮间传播的速度。为减低所需的转速，可让光在两齿轮间多走些路程，这可以借助图 上所示的几面镜子来实现。在这个实验中，当齿轮的转速达到 1000 转每秒时，斐佐从靠近自己的那个齿轮的齿缝间看到了光线。这说明在这种转速下，光线从这个齿轮到达另一个齿轮时，齿轮的每个齿刚好转过了半个齿距。因为每个齿轮上有 50 个完全一样的齿，所以齿距的一半正好是圆周的 1/100，这样，光线走过这段距离的时间也就是齿轮转一圈所用时间的 1/100。再把光线在两齿间走的路程也考虑进来进行计算，斐佐得到了光速为 300 000 公里每秒或186 000 英里每秒这个结果。

　　按照上面的描述，我们来看看这个计算过程是怎样的。

　　假定光从一个齿轮到另一个齿轮所走过的距离为l，齿轮的转速为f，齿轮的齿数为n，光的传播速度为c，那么按照文章中的描述，有下面的公式：

• 光的传播时间t = l / c
• 由齿轮的转速f得出齿轮转一圈的时间为1/f，那么转一个齿轮的时间为1/nf，因此转半个齿轮的时间t = 1 / 2nf

　　所以，

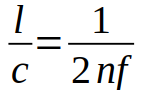
　　得出最终的公式：

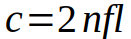
　　已知c=300 000公里每秒，n=50，f=1000转每秒，我们可以得出要成功测算出光速，这个实验装置中光在两个齿轮间传播的距离应为l = c / 2nf，即3公里。考虑到为了使光在两个齿轮间多走些路程，所以实验装置中使用了几面镜子来反射光线，这样齿轮间的距离可以适当缩短些。

　　当然了，从伽利略的方式到斐佐的方式，已经先进了很多，我们也从中看到，物理学家们的智慧，这个智慧不仅仅是在学术理论研究上，也在于对实验装置的精巧设计上。对于光速的测定还有许多其它的方法。