改进版匈牙利算法简介与应用

一、日常生活中常常遇到指派类问题或者分配问题，给N个人员（X1, X2, ... Xn) 安排N份工作（Y1, Y2, ... Yn) ，其中每个人只能胜任其中的若干项工作，而且每个人完成不同工作需要耗费的时间不同。是否可以给每个人分配一个可以胜任的工作，如何分配才能保证完成工作的总耗时最少？类似的场景还有以下几个：

1、男女相亲场景，10男10女为例，可让每人对每个异性进行意向度排序，若是男性优先则可以用男性意向度评分矩阵，女性优先同理，或者使用男女意向评分平均值作为意向度居正，然后用匈牙利算法求最大值，即可获得综合意向度得分最高的分配方法，以下图为列，假设男性优先情况下，每人最终只能选择一位异性匹配，每人也只能被一位异性选择情况下，下图为各男性对各女性有意向度排序后，通过匈牙利算法求解，获得的最终匹配结果，总分达到84分，平均意向度得分8.4

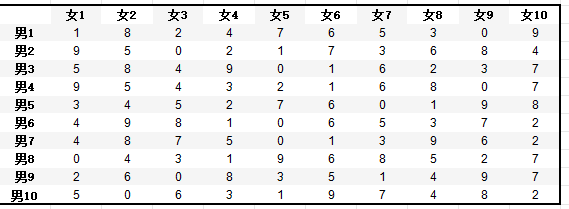
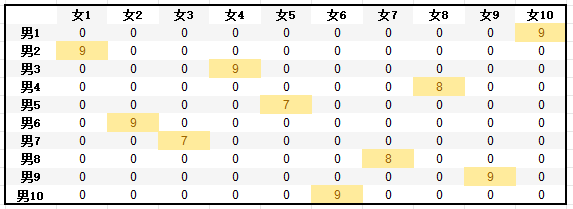
2、电销和催收用户分配场景，不同电销人员对不同类型的客户效果可能催在差异，例如广东人对年长些的广东人电话营销或者催收时可能效果就更好，甜美女性电销人员对某部分男性营销效果更好，则可以根据用户属性和坐席人员属性测算成功概率，通过成功概率矩阵获得成功期望最高的分配方法

3、路径规划场景，例如快递车要去10个地方取件或送件，10个地方都需要经过，如何挑选一个最短的路径，可将每个地点到另一个地点的距离或者耗时算出，用匈牙利算法求得一个最短耗时最小的路径

4、多标签多分类模型评估场景，匈牙利算法可用于多标签多分类场景的评估，例如可用sigmoid函数替代softmax函数，用多个二分类模型获得预测数据对应各标签的预测概率，选定阈值后，获得测试集总体准确率最高的多标签多分类模型

二、算法原理与实现

1、第一步：

(1)查看每行的最小元素的个数总和r和每列的最小元素的个数总和c，并比较r和c的大小
(2)对系数矩阵进行变换，这里的变换是指减去行或列中的最小值，使矩阵在各行各列中都出现0，当r>=c时，先进行列变换，再进行行变换，当r小于等于c时，先进行行变换，再进行列变换

import numpy as np

x=np.array([[12,7,9,7,9],[8,9,6,6,6],[7,17,12,14,9],[15,14,6,6,10],[4,10,7,10,9]])
def get_new_mat(x):
    row_min=x.min(axis=1) #求每行最小值
    col_min=x.min(axis=0) #求每列最小值
    #计算等于行最小值的个数r
    r=0
    for i in range(x.shape[0]):
        for j in x[i,:]:
            if j == row_min[i]:
                r=r+1

#计算等于列最小值的个数r
c=0
for i in range(x.shape[0]):
for j in x[:,i]:
if j == col_min[i]:
c=c+1

                
    #判断行列等于最小值的个数，决定先进性行变换还是列变换
    if r>=c:
        x2=x-col_min[np.newaxis, :]
    else:
        x2=x-row_min[:, np.newaxis]

    #再次进行行列变换，使得每行每列都有0元素
    row_min2=x2.min(axis=1)
    col_min2=x2.min(axis=0)
    if r>=c:
        x3=x2-row_min2[:, np.newaxis]
    else:
        x3=x2-col_min2[np.newaxis,:]
    return x3

x2=get_new_mat(x)
print (x2)

#

[[ 8  0  3  1  3]
 [ 4  2  0  0  0]
 [ 0  7  3  5  0]
 [11  7  0  0  4]
 [ 0  3  1  4  3]]

2、第二步：进行试指派，以寻求最优解。
在系数矩阵中找尽可能多的独立0元素，若能找出n个独立0元素，就以这n个独立0元素对应解矩阵中的元素为1，其余为0，这就得到最优解。找独立0元素，常用的步骤为：
(1)从只有一个0元素的行(列)开始，给这个0元素加圈，记作◎ 。然后划去◎ 所在列(行)的其它0元素，记作Ø ；这表示这列所代表的任务已指派完，不必再考虑别人了（有bug）。
(2)给只有一个0元素的列(行)中的0元素加圈，记作◎；然后划去◎ 所在行的0元素，记作Ø ．
(3)反复进行(1)，(2)两步，直到尽可能多的0元素都被圈出和划掉为止，以下示例代码中用1代替◎，-1代替0

import copy
def get_res(matrix):
    x2=copy.deepcopy(matrix)
    dim= x2.shape[0]
    
    while 1:
        row_zeros = (x2 == 0).sum(axis=1)
        col_zeros = (x2 == 0).sum(axis=0)    
        if (1 not in row_zeros) and (1 not in col_zeros): #判断是否每行每列都没有独立0元素了，都没有则返回结果
            return x2
        elif 1  in row_zeros:   #判断是否每行已没有0元素
            for i in reversed(range(dim)):   
                if list(x2[i,:]).count(0) ==1:
                    o_index=list(x2[i,:]).index(0)        
                    x2[i,] = -1
                    x2[:,o_index] = -1
                    x2[i,o_index] = 1
        elif 1 in col_zeros:  #判断是否每列已无独立0元素
            for j in reversed(range(dim)):
                if list(x2[:,j]).count(0) ==1:
                    o_index=list(x2[:,j]).index(0)
                    x2[:,j] = -1
                    x2[o_index,] = -1
                    x2[o_index,j] = 1
res=get_res(x2) #获得指派结果，可能存在多个最优解,该伪代码存在多个分配最优解时有问题
print ("res")
print (res)
res[1,2]=-1 #随机将其中一个0元素赋值为非0，即可得到其中一个最优解
res1=get_res(res)
res1[res1==-1]=0
print("res1")
print(res1)

[[ 8  0  3  1  3]
 [ 4  2  0  0  0]
 [ 0  7  3  5  0]
 [11  7  0  0  4]
 [ 0  3  1  4  3]]
res
[[-1  1 -1 -1 -1]
 [-1 -1  0  0 -1]
 [-1 -1 -1 -1  1]
 [-1 -1  0  0 -1]
 [ 1 -1 -1 -1 -1]]
res1
[[0 1 0 0 0]
 [0 0 0 1 0]
 [0 0 0 0 1]
 [0 0 1 0 0]
 [1 0 0 0 0]]

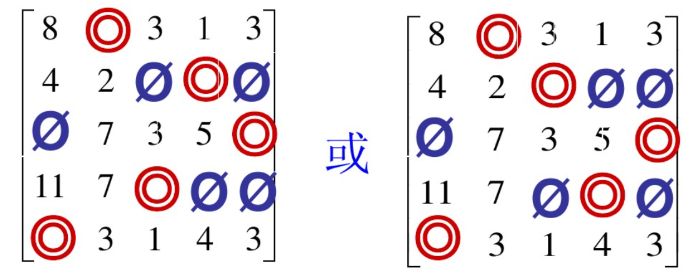
参考资料：https://wenku.baidu.com/aggs/835d8dea998fcc22bcd10d7a.html?_wkts_=1696671115057&bdQuery=%E5%8C%88%E7%89%99%E5%88%A9%E7%AE%97%E6%B3%95+%E7%99%BE%E5%BA%A6%E6%96%87%E5%BA%93

3、对于非标准指派问题上，可转化为标准指派问题，具体有以下几种情况

(1)默认算法求最小值，将矩阵值乘以-1即可求得最大值
(2)人多事少，可添加虚拟“事”，所有人在该事情上的系数为0
(3)人少事多，可添加虚拟“人”，所有人在各事情上的系数为0
(4)某人要多件事，复制该人，该人对所有事情的效益值复制
(5)某人不想做某事，将效益值设为最大值或者最小值

三、python三方包案例

1、使用scipy，求得效益总体最大得分配方法

from random import sample
from scipy.optimize import linear_sum_assignment
import numpy as np

#生成一个10*10的矩阵，每行由不重复的0-9数字组成

matrix = np.zeros((10, 10), dtype=int)
for i in range(10):
    row = sample(range(10), 10) 
    matrix[i] = row
    
#获得每行分配的结果,其中row_ind为顺序
row_ind, col_ind = linear_sum_assignment(-1*matrix)
print (col_ind)

result = np.zeros(matrix.shape)
result[row_ind, col_ind] = 1
print(result)

res=result*matrix
print(res.sum())

#输出
[4 8 5 0 6 3 9 1 7 2]
[[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]]
81.0

2、使用munkres

import munkres
# Use Munkres to compute the indices of the minimum cost pairings
m = munkres.Munkres()
indexes = m.compute(-1*matrix)
print(indexes)

# Parse the results 
result = np.zeros(matrix.shape)
for row, col in indexes:
    result[row, col] = 1

print (result)
res=result*matrix
res.sum()

#输出
[(0, 4), (1, 8), (2, 5), (3, 0), (4, 6), (5, 3), (6, 9), (7, 1), (8, 7), (9, 2)]
[[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]]
81.0

posted @ 2023-10-08 11:01 glowwormss 阅读(547) 评论(0) 编辑收藏举报

刷新页面返回顶部

永远抽象派

改进版匈牙利算法简介与应用

公告