准确率、精确轨、召回率等
链接:https://www.zhihu.com/question/30643044/answer/224360465
正好最近刚做了个项目是关于imbalanced data的,又深入研究了一把各种evaluation metric,在这儿分享一下。
为了方便,以下专业名词都用英文替代了。本人留学狗,脑子不好使容易蹦英文单词,不喜勿喷哈。
准确率 - accuracy
精确率 - precision
召回率 - recall
F1值 - F1-score
ROC曲线下面积 - ROC-AUC (area under curve)
PR曲线下面积 - PR-AUC
首先,accuracy是最常见也是最基本的evaluation metric。但在binary classification 且正反例不平衡的情况下,尤其是我们对minority class 更感兴趣的时候,accuracy评价基本没有参考价值。什么fraud detection(欺诈检测),癌症检测,都符合这种情况。举个栗子:
在测试集里,有100个sample,99个反例,只有1个正例。如果我的模型不分青红皂白对任意一个sample都预测是反例,那么我的模型的accuracy是 正确的个数/总个数 = 99/100 = 99%
你拿着这个accuracy高达99%的模型屁颠儿屁颠儿的去预测新sample了,而它一个正例都分不出来,有意思么。。。
也有人管这叫accuracy paradox。
那么,除了accuracy以外有没有什么别的更有用的metric呢?
有,precision 和 recall。上个图帮助说明一下。
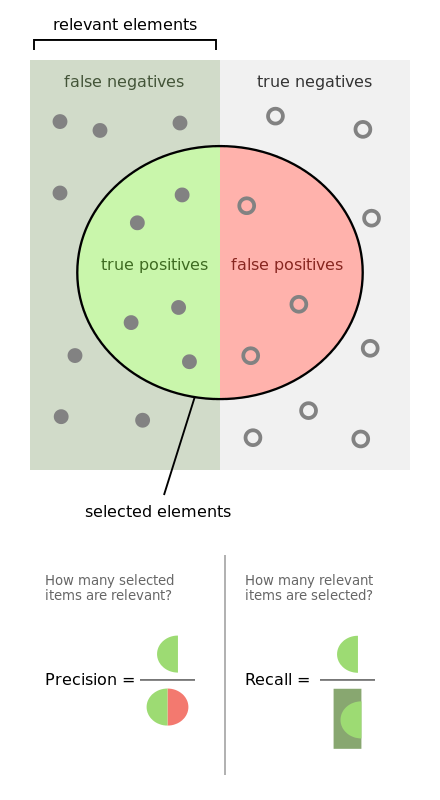
我的理解呢,就是,
- recall是相对真实的答案而言: true positive / golden set 。假设测试集里面有100个正例,你的模型能预测覆盖到多少,如果你的模型预测到了40个正例,那你的recall就是40%。
- precision是相对你自己的模型预测而言:true positive /retrieved set。假设你的模型一共预测了100个正例,而其中80个是对的正例,那么你的precision就是80%。我们可以把precision也理解为,当你的模型作出一个新的预测时,它的confidence score 是多少,或者它做的这个预测是对的的可能性是多少。
- 一般来说呢,鱼与熊掌不可兼得。如果你的模型很贪婪,想要覆盖更多的sample,那么它就更有可能犯错。在这种情况下,你会有很高的recall,但是较低的precision。如果你的模型很保守,只对它很sure的sample作出预测,那么你的precision会很高,但是recall会相对低。
这样一来呢,我们可以选择只看我们感兴趣的class,就是minority class的precision,recall来评价模型的好坏。
F1-score 就是一个综合考虑precision和recall的metric: 2*precision*recall / (precision + recall)
基本上呢,问题就是如果你的两个模型,一个precision特别高,recall特别低,另一个recall特别高,precision特别低的时候,f1-score可能是差不多的,你也不能基于此来作出选择。
在multi-class classification的情况下,如果非要用一个综合考量的metric的话,macro-average(宏平均) 会比 micro-average(微平均) 好一些哦,因为macro会受minority class影响更大,也就是说更能体现在small class上的performance。macro and micro
除了precision,recall,还有别的metric哦。基本上就是把true positive,true negative,false positive,false negative各种瞎JB组合。。
这里介绍两个ROC curve会见到的:sensitivity和specificity。
sensitivity = recall = true positive rate
specificity = 1- false positive rate
这两个metric有什么高级的呢?且听我细细说来。
假设我们的minority class,也就是正例,是1。反例,为0。
是真实label Y的估计(estimate)。

看出来没有,sensitivity和specificity是条件于真实label Y的概率的。我们讲这个叫条件概率嘛。那么意思就是说,无论Y的真实概率是多少,都不会影响sensitivity和specificity。也就是说,这两个metric是不会受imbalanced data 影响的,那就很客观了啊,是不是!而precision呢,就会随着你的测试集里面的正反比例而变化哦。
好了,终于说到我们的ROC curve了。这个曲线呢,就是以true positive rate 和 false positive rate为轴,取不同的threshold点画的啦。有人问了,threshold是啥子哦。这么说吧,每个分类器作出的预测呢,都是基于一个probability score的。一般默认的threshold呢都是0.5,如果probability>0.5,那么这个sample被模型分成正例了哈,反之则是反例。
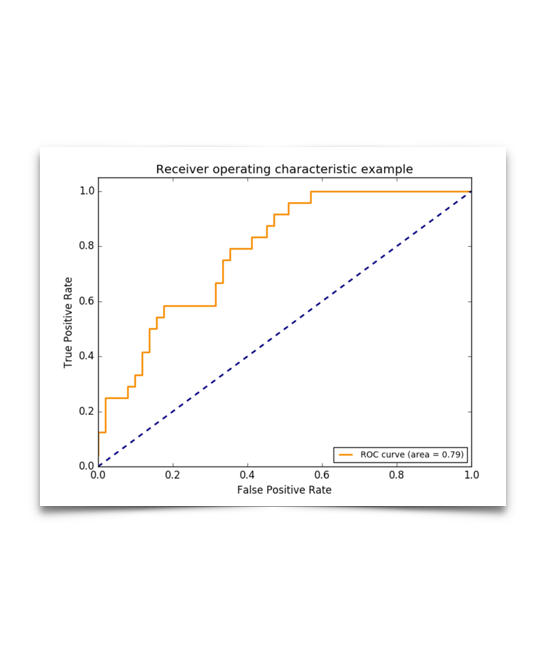
关于这个曲线,大家答的已经很充分了。基本上,曲线下的面积(AUC)越大,或者说曲线更接近左上角(true positive rate=1, false positive rate=0),那么模型就越理想,越好。ROC curve 可以很好的回答什么问题呢——“不论class的基本概率怎么样,我的模型in general能表现得多好?”
一般来说呢,最优的threshold就是橙色曲线离蓝色虚线(基准线)最远的一点啦,或者橙色曲线上离左上角最近的一点,再或者是根据用户自己定义的cost function来的。这里有详细的具体怎么实现。http://www.medicalbiostatistics.com/roccurve.pdf
相对的, 还有一个PR curve,就是以precision recall为轴,取不同的threshold画的哈。刚才说的鱼与熊掌不可兼得的trade-off也可以看的出来哈。
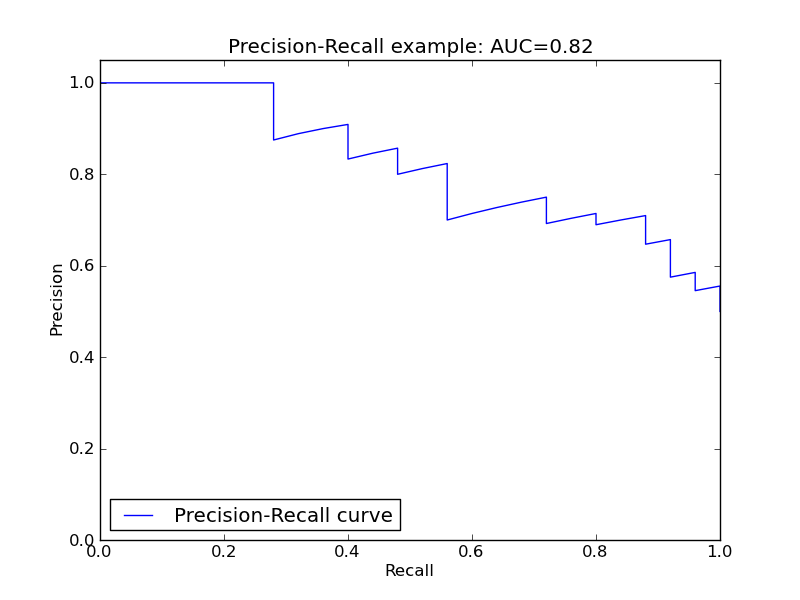
同样的,曲线下的面积(AUC)越大,或者说曲线更接近右上角(precision=1, recall=1),那么模型就越理想,越好。
如果在我们所说的fraud detection 或者癌症检测这一类应用中,我们的倾向肯定是“宁可错杀一千,不可放过一个”呀。所以我们可以设定在合理的precision下,最高的recall作为最优点,找到这个对应的threshold点。
总结,我们可以根据具体的应用或者偏好,在曲线上找到最优的点,得到相对应的precision,recall,sensitivity,specificity,去调整模型的threshold,从而得到一个符合具体应用的模型。
以上。
Reference:
