机器学习(ML)十一之CNN各种模型
深度卷积神经网络(AlexNet)
在LeNet提出后的将近20年里,神经网络一度被其他机器学习方法超越,如支持向量机。虽然LeNet可以在早期的小数据集上取得好的成绩,但是在更大的真实数据集上的表现并不尽如人意。一方面,神经网络计算复杂。虽然20世纪90年代也有过一些针对神经网络的加速硬件,但并没有像之后GPU那样大量普及。因此,训练一个多通道、多层和有大量参数的卷积神经网络在当年很难完成。另一方面,当年研究者还没有大量深入研究参数初始化和非凸优化算法等诸多领域,导致复杂的神经网络的训练通常较困难。
省了很多中间步骤。然而,在很长一段时间里更流行的是研究者通过勤劳与智慧所设计并生成的手工特征。这类图像分类研究的主要流程是:
- 获取图像数据集;
- 使用已有的特征提取函数生成图像的特征;
- 使用机器学习模型对图像的特征分类。
当时认为的机器学习部分仅限最后这一步。如果那时候跟机器学习研究者交谈,他们会认为机器学习既重要又优美。优雅的定理证明了许多分类器的性质。机器学习领域生机勃勃、严谨而且极其有用。然而,如果跟计算机视觉研究者交谈,则是另外一幅景象。他们会告诉你图像识别里“不可告人”的现实是:计算机视觉流程中真正重要的是数据和特征。也就是说,使用较干净的数据集和较有效的特征甚至比机器学习模型的选择对图像分类结果的影响更大。
学习特征表示
相当长的时间里,特征都是基于各式各样手工设计的函数从数据中提取的。事实上,不少研究者通过提出新的特征提取函数不断改进图像分类结果。这一度为计算机视觉的发展做出了重要贡献。
然而,另一些研究者则持异议。他们认为特征本身也应该由学习得来。他们还相信,为了表征足够复杂的输入,特征本身应该分级表示。持这一想法的研究者相信,多层神经网络可能可以学得数据的多级表征,并逐级表示越来越抽象的概念或模式。在多层神经网络中,图像的第一级的表示可以是在特定的位置和⻆度是否出现边缘;而第二级的表示说不定能够将这些边缘组合出有趣的模式,如花纹;在第三级的表示中,也许上一级的花纹能进一步汇合成对应物体特定部位的模式。这样逐级表示下去,最终,模型能够较容易根据最后一级的表示完成分类任务。需要强调的是,输入的逐级表示由多层模型中的参数决定,而这些参数都是学出来的。
尽管一直有一群执着的研究者不断钻研,试图学习视觉数据的逐级表征,然而很长一段时间里这些野心都未能实现。这其中有诸多因素值得我们一一分析。
缺失要素一:数据
包含许多特征的深度模型需要大量的有标签的数据才能表现得比其他经典方法更好。限于早期计算机有限的存储和90年代有限的研究预算,大部分研究只基于小的公开数据集。例如,不少研究论文基于加州大学欧文分校(UCI)提供的若干个公开数据集,其中许多数据集只有几百至几千张图像。这一状况在2010年前后兴起的大数据浪潮中得到改善。特别是,2009年诞生的ImageNet数据集包含了1,000大类物体,每类有多达数千张不同的图像。这一规模是当时其他公开数据集无法与之相提并论的。ImageNet数据集同时推动计算机视觉和机器学习研究进入新的阶段,使此前的传统方法不再有优势。
缺失要素二:硬件
深度学习对计算资源要求很高。早期的硬件计算能力有限,这使训练较复杂的神经网络变得很困难。然而,通用GPU的到来改变了这一格局。很久以来,GPU都是为图像处理和计算机游戏设计的,尤其是针对大吞吐量的矩阵和向量乘法从而服务于基本的图形变换。值得庆幸的是,这其中的数学表达与深度网络中的卷积层的表达类似。通用GPU这个概念在2001年开始兴起,涌现出诸如OpenCL和CUDA之类的编程框架。这使得GPU也在2010年前后开始被机器学习社区使用。
AlexNet
2012年,AlexNet横空出世。这个模型的名字来源于论文第一作者的姓名Alex Krizhevsky [1]。AlexNet使用了8层卷积神经网络,并以很大的优势赢得了ImageNet 2012图像识别挑战赛。它首次证明了学习到的特征可以超越手工设计的特征,从而一举打破计算机视觉研究的前状。
AlexNet与LeNet的设计理念非常相似,但也有显著的区别。
第一,与相对较小的LeNet相比,AlexNet包含8层变换,其中有5层卷积和2层全连接隐藏层,以及1个全连接输出层。下面我们来详细描述这些层的设计。
AlexNet第一层中的卷积窗口形状是11×11。因为ImageNet中绝大多数图像的高和宽均比MNIST图像的高和宽大10倍以上,ImageNet图像的物体占用更多的像素,所以需要更大的卷积窗口来捕获物体。第二层中的卷积窗口形状减小到5×55×5,之后全采用3×3。此外,第一、第二和第五个卷积层之后都使用了窗口形状为3×3、步幅为2的最大池化层。而且,AlexNet使用的卷积通道数也大于LeNet中的卷积通道数数十倍。
紧接着最后一个卷积层的是两个输出个数为4096的全连接层。这两个巨大的全连接层带来将近1 GB的模型参数。由于早期显存的限制,最早的AlexNet使用双数据流的设计使一个GPU只需要处理一半模型。幸运的是,显存在过去几年得到了长足的发展,因此通常我们不再需要这样的特别设计了。
第二,AlexNet将sigmoid激活函数改成了更加简单的ReLU激活函数。一方面,ReLU激活函数的计算更简单,例如它并没有sigmoid激活函数中的求幂运算。另一方面,ReLU激活函数在不同的参数初始化方法下使模型更容易训练。这是由于当sigmoid激活函数输出极接近0或1时,这些区域的梯度几乎为0,从而造成反向传播无法继续更新部分模型参数;而ReLU激活函数在正区间的梯度恒为1。因此,若模型参数初始化不当,sigmoid函数可能在正区间得到几乎为0的梯度,从而令模型无法得到有效训练。
第三,AlexNet通过丢弃法来控制全连接层的模型复杂度。而LeNet并没有使用丢弃法。
第四,AlexNet引入了大量的图像增广,如翻转、裁剪和颜色变化,从而进一步扩大数据集来缓解过拟合。
- AlexNet跟LeNet结构类似,但使用了更多的卷积层和更大的参数空间来拟合大规模数据集ImageNet。它是浅层神经网络和深度神经网络的分界线。
- 虽然看上去AlexNet的实现比LeNet的实现也就多了几行代码而已,但这个观念上的转变和真正优秀实验结果的产生令学术界付出了很多年。
AlexNet代码实现

1 #alexnet模型 2 import d2lzh as d2l 3 from mxnet import gluon, init, nd 4 from mxnet.gluon import data as gdata, nn 5 import os 6 import sys 7 8 net = nn.Sequential() 9 # 使用较大的11 x 11窗口来捕获物体。同时使用步幅4来较大幅度减小输出高和宽。这里使用的输出通 10 # 道数比LeNet中的也要大很多 11 net.add(nn.Conv2D(96, kernel_size=11, strides=4, activation='relu'), 12 nn.MaxPool2D(pool_size=3, strides=2), 13 # 减小卷积窗口,使用填充为2来使得输入与输出的高和宽一致,且增大输出通道数 14 nn.Conv2D(256, kernel_size=5, padding=2, activation='relu'), 15 nn.MaxPool2D(pool_size=3, strides=2), 16 # 连续3个卷积层,且使用更小的卷积窗口。除了最后的卷积层外,进一步增大了输出通道数。 17 # 前两个卷积层后不使用池化层来减小输入的高和宽 18 nn.Conv2D(384, kernel_size=3, padding=1, activation='relu'), 19 nn.Conv2D(384, kernel_size=3, padding=1, activation='relu'), 20 nn.Conv2D(256, kernel_size=3, padding=1, activation='relu'), 21 nn.MaxPool2D(pool_size=3, strides=2), 22 # 这里全连接层的输出个数比LeNet中的大数倍。使用丢弃层来缓解过拟合 23 nn.Dense(4096, activation="relu"), nn.Dropout(0.5), 24 nn.Dense(4096, activation="relu"), nn.Dropout(0.5), 25 # 输出层。由于这里使用Fashion-MNIST,所以用类别数为10,而非论文中的1000 26 nn.Dense(10)) 27 28 X = nd.random.uniform(shape=(1, 1, 224, 224)) 29 net.initialize() 30 for layer in net: 31 X = layer(X) 32 print(layer.name, 'output shape:\t', X.shape) 33 34 # 本函数已保存在d2lzh包中方便以后使用 35 #Fashion-MNIST数据集来演示AlexNet。读取数据的时候我们额外做了一步将图像高和宽扩大到AlexNet使用的图像高和宽224。 36 #这个可以通过Resize实例来实现。也就是说,我们在ToTensor实例前使用Resize实例, 37 #然后使用Compose实例来将这两个变换串联以方便调用。 38 39 def load_data_fashion_mnist(batch_size, resize=None, root=os.path.join( 40 '~', '.mxnet', 'datasets', 'fashion-mnist')): 41 root = os.path.expanduser(root) # 展开用户路径'~' 42 transformer = [] 43 if resize: 44 transformer += [gdata.vision.transforms.Resize(resize)] 45 transformer += [gdata.vision.transforms.ToTensor()] 46 transformer = gdata.vision.transforms.Compose(transformer) 47 mnist_train = gdata.vision.FashionMNIST(root=root, train=True) 48 mnist_test = gdata.vision.FashionMNIST(root=root, train=False) 49 num_workers = 0 if sys.platform.startswith('win32') else 4 50 train_iter = gdata.DataLoader( 51 mnist_train.transform_first(transformer), batch_size, shuffle=True, 52 num_workers=num_workers) 53 test_iter = gdata.DataLoader( 54 mnist_test.transform_first(transformer), batch_size, shuffle=False, 55 num_workers=num_workers) 56 return train_iter, test_iter 57 58 batch_size = 128 59 # 如出现“out of memory”的报错信息,可减小batch_size或resize 60 train_iter, test_iter = load_data_fashion_mnist(batch_size, resize=224) 61 62 lr, num_epochs, ctx = 0.01, 5, d2l.try_gpu() 63 net.initialize(force_reinit=True, ctx=ctx, init=init.Xavier()) 64 trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': lr}) 65 d2l.train_ch5(net, train_iter, test_iter, batch_size, trainer, ctx, num_epochs)
使用重复元素的网络(VGG)
AlexNet在LeNet的基础上增加了3个卷积层。但AlexNet作者对它们的卷积窗口、输出通道数和构造顺序均做了大量的调整。虽然AlexNet指明了深度卷积神经网络可以取得出色的结果,但并没有提供简单的规则以指导后来的研究者如何设计新的网络。我们将在本章的后续几节里介绍几种不同的深度网络设计思路。
本节介绍VGG,它的名字来源于论文作者所在的实验室Visual Geometry Group。VGG提出了可以通过重复使用简单的基础块来构建深度模型的思路。
VGG块
VGG块的组成规律是:连续使用数个相同的填充为1、窗口形状为3×3的卷积层后接上一个步幅为2、窗口形状为2×2的最大池化层。卷积层保持输入的高和宽不变,而池化层则对其减半。我们使用vgg_block函数来实现这个基础的VGG块,它可以指定卷积层的数量num_convs和输出通道数num_channels。
VGG网络
与AlexNet和LeNet一样,VGG网络由卷积层模块后接全连接层模块构成。卷积层模块串联数个vgg_block,其超参数由变量conv_arch定义。该变量指定了每个VGG块里卷积层个数和输出通道数。全连接模块则跟AlexNet中的一样。
- VGG-11通过5个可以重复使用的卷积块来构造网络。根据每块里卷积层个数和输出通道数的不同可以定义出不同的VGG模型。
VGG模型代码实现

1 #vgg网络模型 2 import d2lzh as d2l 3 from mxnet import gluon, init, nd 4 from mxnet.gluon import nn 5 6 def vgg_block(num_convs, num_channels): 7 blk = nn.Sequential() 8 for _ in range(num_convs): 9 blk.add(nn.Conv2D(num_channels, kernel_size=3, 10 padding=1, activation='relu')) 11 blk.add(nn.MaxPool2D(pool_size=2, strides=2)) 12 return blk 13 conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512)) 14 def vgg(conv_arch): 15 net = nn.Sequential() 16 # 卷积层部分 17 for (num_convs, num_channels) in conv_arch: 18 net.add(vgg_block(num_convs, num_channels)) 19 # 全连接层部分 20 net.add(nn.Dense(4096, activation='relu'), nn.Dropout(0.5), 21 nn.Dense(4096, activation='relu'), nn.Dropout(0.5), 22 nn.Dense(10)) 23 return net 24 25 net = vgg(conv_arch) 26 net.initialize() 27 X = nd.random.uniform(shape=(1, 1, 224, 224)) 28 for blk in net: 29 X = blk(X) 30 print(blk.name, 'output shape:\t', X.shape) 31 ratio = 4 32 small_conv_arch = [(pair[0], pair[1] // ratio) for pair in conv_arch] 33 net = vgg(small_conv_arch) 34 lr, num_epochs, batch_size, ctx = 0.05, 5, 128, d2l.try_gpu() 35 net.initialize(ctx=ctx, init=init.Xavier()) 36 trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': lr}) 37 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224) 38 d2l.train_ch5(net, train_iter, test_iter, batch_size, trainer, ctx, 39 num_epochs)
网络中的网络(NiN)
LeNet、AlexNet和VGG在设计上的共同之处是:先以由卷积层构成的模块充分抽取空间特征,再以由全连接层构成的模块来输出分类结果。其中,AlexNet和VGG对LeNet的改进主要在于如何对这两个模块加宽(增加通道数)和加深。本节我们介绍网络中的网络(NiN)。它提出了另外一个思路,即串联多个由卷积层和“全连接”层构成的小网络来构建一个深层网络。
卷积层的输入和输出通常是四维数组(样本,通道,高,宽),而全连接层的输入和输出则通常是二维数组(样本,特征)。如果想在全连接层后再接上卷积层,则需要将全连接层的输出变换为四维。它可以看成全连接层,其中空间维度(高和宽)上的每个元素相当于样本,通道相当于特征。因此,NiN使用1×1卷积层来替代全连接层,从而使空间信息能够自然传递到后面的层中去。下图对比了NiN同AlexNet和VGG等网络在结构上的主要区别。
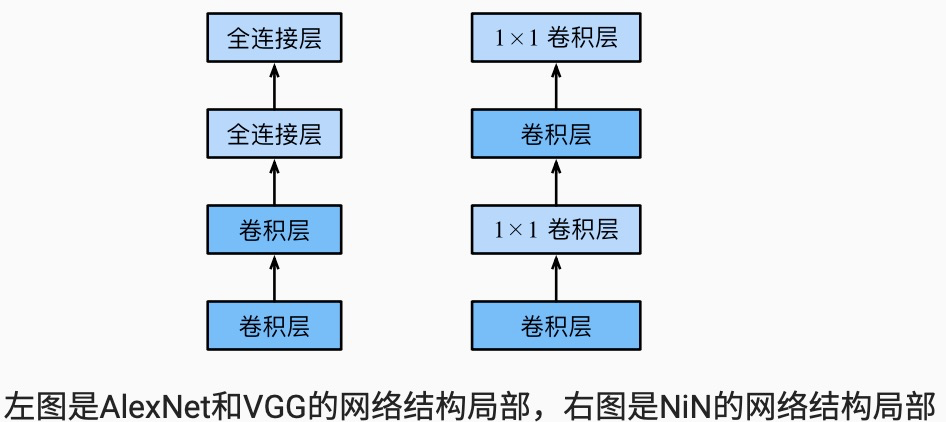
NiN块是NiN中的基础块。它由一个卷积层加两个充当全连接层的1×1卷积层串联而成。其中第一个卷积层的超参数可以自行设置,而第二和第三个卷积层的超参数一般是固定的。
NiN模型
NiN是在AlexNet问世不久后提出的。它们的卷积层设定有类似之处。NiN使用卷积窗口形状分别为11×11、5×5和3×3的卷积层,相应的输出通道数也与AlexNet中的一致。每个NiN块后接一个步幅为2、窗口形状为3×3的最大池化层。
除使用NiN块以外,NiN还有一个设计与AlexNet显著不同:NiN去掉了AlexNet最后的3个全连接层,取而代之地,NiN使用了输出通道数等于标签类别数的NiN块,然后使用全局平均池化层对每个通道中所有元素求平均并直接用于分类。这里的全局平均池化层即窗口形状等于输入空间维形状的平均池化层。NiN的这个设计的好处是可以显著减小模型参数尺寸,从而缓解过拟合。然而,该设计有时会造成获得有效模型的训练时间的增加。
- NiN重复使用由卷积层和代替全连接层的
- 1×1卷积层构成的NiN块来构建深层网络。
- NiN去除了容易造成过拟合的全连接输出层,而是将其替换成输出通道数等于标签类别数的NiN块和全局平均池化层。
- NiN的以上设计思想影响了后面一系列卷积神经网络的设计。
NiN模型代码实现

1 #nin模型实现 2 import d2lzh as d2l 3 from mxnet import gluon, init, nd 4 from mxnet.gluon import nn 5 6 def nin_block(num_channels, kernel_size, strides, padding): 7 blk = nn.Sequential() 8 blk.add(nn.Conv2D(num_channels, kernel_size, 9 strides, padding, activation='relu'), 10 nn.Conv2D(num_channels, kernel_size=1, activation='relu'), 11 nn.Conv2D(num_channels, kernel_size=1, activation='relu')) 12 return blk 13 net = nn.Sequential() 14 net.add(nin_block(96, kernel_size=11, strides=4, padding=0), 15 nn.MaxPool2D(pool_size=3, strides=2), 16 nin_block(256, kernel_size=5, strides=1, padding=2), 17 nn.MaxPool2D(pool_size=3, strides=2), 18 nin_block(384, kernel_size=3, strides=1, padding=1), 19 nn.MaxPool2D(pool_size=3, strides=2), nn.Dropout(0.5), 20 # 标签类别数是10 21 nin_block(10, kernel_size=3, strides=1, padding=1), 22 # 全局平均池化层将窗口形状自动设置成输入的高和宽 23 nn.GlobalAvgPool2D(), 24 # 将四维的输出转成二维的输出,其形状为(批量大小, 10) 25 nn.Flatten()) 26 X = nd.random.uniform(shape=(1, 1, 224, 224)) 27 net.initialize() 28 for layer in net: 29 X = layer(X) 30 print(layer.name, 'output shape:\t', X.shape) 31 lr, num_epochs, batch_size, ctx = 0.1, 5, 128, d2l.try_gpu() 32 net.initialize(force_reinit=True, ctx=ctx, init=init.Xavier()) 33 trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': lr}) 34 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224) 35 d2l.train_ch5(net, train_iter, test_iter, batch_size, trainer, ctx, 36 num_epochs)
含并行连结的网络(GoogLeNet)
在2014年的ImageNet图像识别挑战赛中,一个名叫GoogLeNet的网络结构大放异彩 。它虽然在名字上向LeNet致敬,但在网络结构上已经很难看到LeNet的影子。GoogLeNet吸收了NiN中网络串联网络的思想,并在此基础上做了很大改进。在随后的几年里,研究人员对GoogLeNet进行了数次改进,本节将介绍这个模型系列的第一个版本。
Inception 块
GoogLeNet中的基础卷积块叫作Inception块,得名于同名电影《盗梦空间》(Inception)。与上一节介绍的NiN块相比,这个基础块在结构上更加复杂。

可以看出,Inception块里有4条并行的线路。前3条线路使用窗口大小分别是1×1、3×3和5×5的卷积层来抽取不同空间尺寸下的信息,其中中间2个线路会对输入先做1×1卷积来减少输入通道数,以降低模型复杂度。第四条线路则使用3×3最大池化层,后接1×1卷积层来改变通道数。4条线路都使用了合适的填充来使输入与输出的高和宽一致。最后我们将每条线路的输出在通道维上连结,并输入接下来的层中去。
Inception块中可以自定义的超参数是每个层的输出通道数,我们以此来控制模型复杂度。
GoogLeNet模型
GoogLeNet跟VGG一样,在主体卷积部分中使用5个模块(block),每个模块之间使用步幅为2的3×3最大池化层来减小输出高宽。第一模块使用一个64通道的7×7卷积层。
- inception块相当于一个有4条线路的子网络。它通过不同窗口形状的卷积层和最大池化层来并行抽取信息,并使用
- 1×1卷积层减少通道数从而降低模型复杂度。
- GoogLeNet将多个设计精细的Inception块和其他层串联起来。其中Inception块的通道数分配之比是在ImageNet数据集上通过大量的实验得来的。
- GoogLeNet和它的后继者们一度是ImageNet上最高效的模型之一:在类似的测试精度下,它们的计算复杂度往往更低。
GoogLeNet模型代码实现

1 import d2lzh as d2l 2 from mxnet import gluon, init, nd 3 from mxnet.gluon import nn 4 5 class Inception(nn.Block): 6 # c1 - c4为每条线路里的层的输出通道数 7 def __init__(self, c1, c2, c3, c4, **kwargs): 8 super(Inception, self).__init__(**kwargs) 9 # 线路1,单1 x 1卷积层 10 self.p1_1 = nn.Conv2D(c1, kernel_size=1, activation='relu') 11 # 线路2,1 x 1卷积层后接3 x 3卷积层 12 self.p2_1 = nn.Conv2D(c2[0], kernel_size=1, activation='relu') 13 self.p2_2 = nn.Conv2D(c2[1], kernel_size=3, padding=1, 14 activation='relu') 15 # 线路3,1 x 1卷积层后接5 x 5卷积层 16 self.p3_1 = nn.Conv2D(c3[0], kernel_size=1, activation='relu') 17 self.p3_2 = nn.Conv2D(c3[1], kernel_size=5, padding=2, 18 activation='relu') 19 # 线路4,3 x 3最大池化层后接1 x 1卷积层 20 self.p4_1 = nn.MaxPool2D(pool_size=3, strides=1, padding=1) 21 self.p4_2 = nn.Conv2D(c4, kernel_size=1, activation='relu') 22 23 def forward(self, x): 24 p1 = self.p1_1(x) 25 p2 = self.p2_2(self.p2_1(x)) 26 p3 = self.p3_2(self.p3_1(x)) 27 p4 = self.p4_2(self.p4_1(x)) 28 return nd.concat(p1, p2, p3, p4, dim=1) # 在通道维上连结输出 29 #googlenet模型 30 b1 = nn.Sequential() 31 b1.add(nn.Conv2D(64, kernel_size=7, strides=2, padding=3, activation='relu'), 32 nn.MaxPool2D(pool_size=3, strides=2, padding=1)) 33 #第二模块使用2个卷积层:首先是64通道的 1×1 卷积层,然后是将通道增大3倍的 3×3 卷积层。它对应Inception块中的第二条线路。 34 b2 = nn.Sequential() 35 b2.add(nn.Conv2D(64, kernel_size=1, activation='relu'), 36 nn.Conv2D(192, kernel_size=3, padding=1, activation='relu'), 37 nn.MaxPool2D(pool_size=3, strides=2, padding=1)) 38 b3 = nn.Sequential() 39 b3.add(Inception(64, (96, 128), (16, 32), 32), 40 Inception(128, (128, 192), (32, 96), 64), 41 nn.MaxPool2D(pool_size=3, strides=2, padding=1)) 42 b4 = nn.Sequential() 43 b4.add(Inception(192, (96, 208), (16, 48), 64), 44 Inception(160, (112, 224), (24, 64), 64), 45 Inception(128, (128, 256), (24, 64), 64), 46 Inception(112, (144, 288), (32, 64), 64), 47 Inception(256, (160, 320), (32, 128), 128), 48 nn.MaxPool2D(pool_size=3, strides=2, padding=1)) 49 b5 = nn.Sequential() 50 b5.add(Inception(256, (160, 320), (32, 128), 128), 51 Inception(384, (192, 384), (48, 128), 128), 52 nn.GlobalAvgPool2D()) 53 54 net = nn.Sequential() 55 net.add(b1, b2, b3, b4, b5, nn.Dense(10)) 56 X = nd.random.uniform(shape=(1, 1, 96, 96)) 57 net.initialize() 58 for layer in net: 59 X = layer(X) 60 print(layer.name, 'output shape:\t', X.shape) 61 lr, num_epochs, batch_size, ctx = 0.1, 5, 128, d2l.try_gpu() 62 net.initialize(force_reinit=True, ctx=ctx, init=init.Xavier()) 63 trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': lr}) 64 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96) 65 d2l.train_ch5(net, train_iter, test_iter, batch_size, trainer, ctx, 66 num_epochs)


