机器学习(ML)二之损失函数
一、模型举例
1. 预测政治倾向例子
模型1
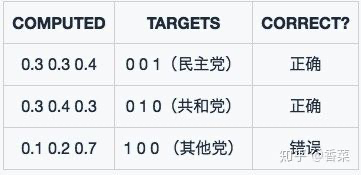
模型1对于样本1和样本2以非常微弱的优势判断正确,对于样本3的判断则彻底错误。
模型2:
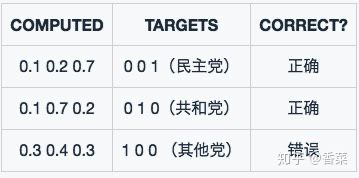
型2对于样本1和样本2判断非常准确,对于样本3判断错误,但是相对来说没有错得太离谱。
二、模型分类
1、Classification Error
损失函数定义为:
模型1:
模型2:
我们知道,模型1和模型2虽然都是预测错了1个,但是相对来说模型2表现得更好,损失函数值照理来说应该更小,但是,很遗憾的是, 并不能判断出来,所以这种损失函数虽然好理解,但表现不太好。
2、Mean Squared Error
均方误差损失也是一种比较常见的损失函数,其定义为:
模型1:
对所有样本的loss求平均:
模型2:
对所有样本的loss求平均:
我们发现,MSE能够判断出来模型2优于模型1,那为什么不采样这种损失函数呢?主要原因是逻辑回归配合MSE损失函数时,采用梯度下降法进行学习时,会出现模型一开始训练时,学习速率非常慢的情况(MSE损失函数)。
有了上面的直观分析,我们可以清楚的看到,对于分类问题的损失函数来说,分类错误率和均方误差损失都不是很好的损失函数,下面我们来看一下交叉熵损失函数的表现情况。
3、Cross Entropy Error Function
3.1 表达式
3.1.1 二分类
在二分的情况下,模型最后需要预测的结果只有两种情况,对于每个类别我们的预测得到的概率为 和
。此时表达式为:
其中:
- y——表示样本的label,正类为1,负类为0
- p——表示样本预测为正的概率
3.1.2 多分类
多分类的情况实际上就是对二分类的扩展:
其中:
- ——类别的数量;
- ——指示变量(0或1),如果该类别和样本的类别相同就是1,否则是0;
- ——对于观测样本属于类别
的预测概率。
现在我们利用这个表达式计算上面例子中的损失函数值:
模型1:
对所有样本的loss求平均:
模型2:
对所有样本的loss求平均:
可以发现,交叉熵损失函数可以捕捉到模型1和模型2预测效果的差异。
3.2 函数性质
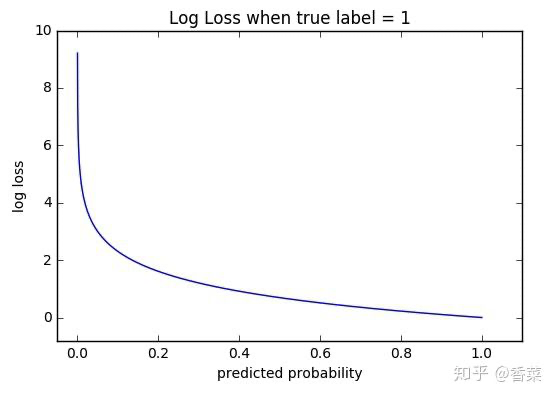
可以看出,该函数是凸函数,求导时能够得到全局最优值。
三. 学习总结
交叉熵损失函数经常用于分类问题中,特别是在神经网络做分类问题时,也经常使用交叉熵作为损失函数,此外,由于交叉熵涉及到计算每个类别的概率,所以交叉熵几乎每次都和sigmoid(或softmax)函数一起出现。
我们用神经网络最后一层输出的情况,来看一眼整个模型预测、获得损失和学习的流程:
- 神经网络最后一层得到每个类别的得分scores;
- 该得分经过sigmoid(或softmax)函数获得概率输出;
- 模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。
四. 参考
[1]. 神经网络的分类模型 LOSS 函数为什么要用 CROSS ENTROPY
[2]. Softmax as a Neural Networks Activation Function


