基于numpy使用梯度下降法解决简单的线性回归问题
基于numpy使用梯度下降法解决简单的线性回归问题
理论推导
使用 \(y=wx\) 作为目标函数
初始化 \(w\) 为某一个值,然后加上噪点生成一组样本
例如初始化 \(w\) 为100,\(x\in[-10, 10]\)
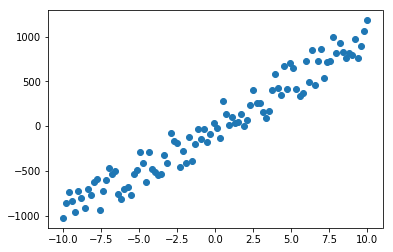
目的是拟合出一条形如 \(y=wx\) 的直线让这条直线尽可能的拟合这组样本点
使用均方差损失函数来表达拟合程度,越小说明拟合的越好
定义总损失函数为
\[\begin{aligned}
loss
&=(\sum_{i=0}^n((y_i^{predict}-y_i)^2))/n \\
&=(\sum_{i=0}^n(wx_i-y_i)^2))/n \\
\end{aligned}
\]
\(n\) 表示样本点的个数,函数的自变量为 \(w\) ,\(loss\) 的梯度为
\[\begin{aligned}
\nabla&=(\frac{\alpha loss}{\alpha w})\\
\frac{\alpha loss}{\alpha w}&=(\sum_{i=0}^n2(wx_i-y_i)x_i)/n \\
\end{aligned}
\]
梯度就是函数值增加最快的方向,我们的目的是让损失函数值,即均方差变小
只需要让 \(loss\) 逆着梯度的方向变化就好,即让 \(loss\) 的每个自变量都减去对应的偏导数
设 \(w\) 每次的变化量为 \(lr*\frac{\alpha loss}{\alpha w}\),\(lr\) 取的越大,\(w\) 的变化率越大,一般取一个较小的值如 \(5e-4\)
即
\[\begin{aligned}
dw&=lr*\frac{\alpha loss}{\alpha w}\\
w&=w-dw
\end{aligned}
\]
只要按照这个公式不断更新 \(w\) ,最终就能得到损失函数的一个最小值
即找到了一条能够很好的拟合样本的直线
代码实现
import numpy as np # 科学计算库
from tqdm import tqdm # 进度条库
import matplotlib.pyplot as plt # 绘图库
# 将预测值、损失值和梯度的计算封装一下
class Model:
def __init__(self, w):
self.w = w
def __call__(self, x):
return self.w*x
def loss(self, y, y1):
return np.mean(np.power(y1-y, 2))
def gradient(self, x, y):
return np.mean(2 * (self(x)-y) * x)
# 超参数
epochs = 100
lr = 0.0005
init_w = 0
train_data = np.linspace(-10, 10, 100)
real_model = Model(100)
train_label = real_model(train_data)
train_label += (np.random.rand(*train_label.shape)-0.5)*500
plt.scatter(train_data, train_label)
plt.show()
# 开始迭代
model = Model(init_w)
losses = {}
with tqdm(total=epochs) as pbar:
for epoch in range(epochs):
y = model(train_data)
loss = model.loss(y, train_label)
losses[model.w] = loss
gradient_w = model.gradient(train_data, train_label)
model.w -= lr*gradient_w
pbar.set_description("loss:{:.2f}, w:{:.2f}".format(loss, model.w))
pbar.update(1)
# 画出样本点、原始直线、预测直线
plt.plot(train_data, real_model(train_data), c="g", label="origin")
plt.scatter(train_data, train_label, label="sample")
plt.plot(train_data, model(train_data), c="r", label="predict")
plt.legend()
plt.show()
# 画出损失函数曲线
w = np.linspace(0, 200, 100)
l = [np.mean(np.power(_w*train_data-train_label, 2)) for _w in w]
plt.plot(w, l, label="loss func")
plt.scatter(list(losses.keys())[::3], list(losses.values())[::3], label="loss")
plt.legend()
plt.show()
扩展
动量(momentum),是一个力学上的词,一般而言,一个物体的动量指的是这个物体在它运动方向上保持运动的趋势。在深度学习中则是一种加快损失函数收敛的方法
\[\begin{aligned}
v_{i+1}&=mu*v_i-lr*dw\\
w_{i+1}&=w_i+v_{i+1}
\end{aligned}
\]
mu是一个常量,一般设为0.9,\(v\) 初始化为0,即
\[\begin{aligned}
v_0&=-lr*dw\\
v_1&=mu*v_0 - lr*dw\\
...\\
v_i&=mu*v_{i-1}-lr*dw
\end{aligned}
\]
如果梯度方向没有改变,\(v\) 将会变得越来越大,也就是 \(w\) 的变化的幅度将会越来越大
这种情况下很有可能一步跨越最小值点,这时梯度方向将会反转,即 \(v_i*v_{i-1}<0\)
\(v\) 又会开始减小,重复以上过程,在不断的震荡中,损失函数值将会趋近于最小值点
将上述代码中的”开始迭代“部分改为下面的代码就可以使用动量
# 开始迭代
model = Model(init_w)
losses = {}
with tqdm(total=epochs) as pbar:
v = 0
for epoch in range(epochs):
y = model(train_data)
loss = model.loss(y, train_label)
losses[model.w] = loss
gradient_w = model.gradient(train_data, train_label)
v = mu*v - lr*gradient_w
model.w += v
pbar.set_description("loss:{:.2f}, w:{:.2f}".format(loss, model.w))
pbar.update(1)


