求和平均统计
单因素方差分析我大白话说就是求和平均统计,样本与平均值进行各种对比得出的结论,如下:
在试验中,把考察的指标称为试验指标,影响试验指标的条件称为因素。因素可分为两类,一类是人为可控的测量数据,比如温度、身高等;一类是不可控的随机因素,例如,测量误差,气象条件等。因素所处的状态称为因素的水平。如果在试验过程中,只有一个因素在改变,称为单因素试验。方差分析(Analysis of Variance,简称ANOVA)主要用于验证两组样本,或者两组以上的样本均值是否有显著性差异(是否一致)。
举个例子,有三台机器用来生产规格相同的铝合金薄板,试验的指标是铝合金薄板的厚度,机器是因素,不同的三台机器是因素的三个水平。试验的目的是为了考察每台机器所生产的薄板的厚度是否有显著的差异,即考察机器这一因素对薄板厚度有无显著的影响,如果厚度有显著差异,就表明机器对厚度的影响是显著的。
一,单因素方差分析
对多个总体均值进行检验,需要用到方差分析方法,例如,某工厂有A、B、C三台轧制板材的设备,如果想知道这三台设备轧制板材的厚度是否一致,就可以转化为检验来自三个总体的均值是否相同的问题。以上面所说轧制板材为例,检验A、B、C三台设备轧制的板材厚度是否一致,可以建立如下假设:
H0: μ1=μ2=…=μr;
H1: μ1,μ2,…,μr不全相等。
三个总体均值是否相等无从知道,但是可以通过样本均值是否有显著差异来检验总体均值是否相等。因为,如果H0为真时,则可以期望样本均值很接近,如果样本均值很接近,则推断总体均值相等的证据很充分,就可以接受H0。否则,当样本均值相距较远,就认为总体均值相等的证据不充分,从而拒绝H0,接受H1。
样本均值之间距离的所谓远近是相对的,是通过假定的共同方差的两个点估计值比较得出的。第一个点估计是组内方差,用各个样本方差估计得到的,只与每个样本内部的方差有关,反映各个水平内部随机性的变动。第二个点估计值是组间方差,在H0为真的前提下,由均值抽样平均误差计算得到,这样得到的方差包含两部分的变动:一是各个水平内部的随机性变动,二是各个水平之间的变动。将组间方差与组内方差相比,可以得到一个F统计量(F=组间方差/组内方差),可以证明该统计量服从F分布。
由推断可知,如果三台设备轧制板材的厚度均值相差很小,即组间方差中的各个水平之间的变动很小,F比值会接近于1。反之,则F的比值会显著地大于1,根据上面计算得到的F值,在显著性水平α给定的情况下,就可以做出是否接受三台设备轧制板材厚度均值相等的假设。
二,单因素方差分析步骤
现在假定一个因素B具有c个水平的因变量进行方差分析检验,例如上面提到的工厂轧制设备是因素,分别试验轧制了10块板材是水平。
c为因变量的个数,如肥料配比不同的个数,nj为当前因素下最后一个实验对象的编号,即改因素下的有几个实验对象,nt为实验的总个数
1、建立假设
H0: μ1=μ2=…=μc;
H1: μ1,μ2,…,μc不全相等。
2、计算样本均值和样本方差

3、计算组间方差

4、组内方差的估计

5、构造F统计量进行检验
F=组间方差/组内方差=MSB/MSE~F(c-1, nT-1)
如果c个总体均值不相等,则组间方差(MSB)会大于组内方差(MSE)。当F值大到某一临界值时,就可以拒绝H0。临界值的大小由给定的α和自由度决定。所以,当给定显著性水平为α时,F的拒绝域为F>Fα(c-1,nT-c)。
6、方差分析表

三,范例分析
例题:有8位食品专家对三种配方的食品随机品尝,然后给食品的口感分别打分(满分10分),如下表。问三种配方的平均分数是否相同?(α=0.05)(假定打分服从标准相等的正态分布)。

解:设μA,μB,μC分别代表配方1、2、3。已知因变量是分数,因素是配方,水平为3,具有相同的样本容量8。根据题意建立假设:
H0: μA=μB=μC;
H1: 总体均值不全相等。
首先,计算样本均值及方差
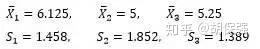
其次,计算组间方差MSB
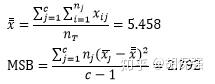
第三,计算组内方差MSE
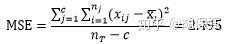
第四,计算F统计量
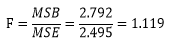
最后,查表Fα(c-1,nT-c)= F0.05(2,21)=3.47。因为F=1.119<3.47= F0.05(2,21),落在接受域。所以接受H0,拒绝H1,即三种配方的口感分数没有显著的差异。


∑为求和符号,下标为开始位置的值,上标为结束位置的值,按照后面的公式进行累加,如
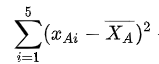
表示:A因素下,从第一个实验对象的值减去平均值的平方,一直加到最后一个实验对象的值与平均值的差值平方,
Java代码实现如下:
public static void main(String[] args) { double x = (8 + 4 + 5 + 6 + 7 + 8 + 6 + 5 + 6 + 2 + 7 + 5 + 3 + 7 + 4 + 6 + 5 + 7 + 6 + 3 + 4 + 7 + 5 + 5) / 24.00D; System.out.println("x均值:" + x); double x1 = (8 + 4 + 5 + 6 + 7 + 8 + 6 + 5) / 8.00D; System.out.println("x1均值:" + x1); double x2 = (6 + 2 + 7 + 5 + 3 + 7 + 4 + 6) / 8.00D; System.out.println("x2均值:" + x2); double x3 = (5 + 7 + 6 + 3 + 4 + 7 + 5 + 5) / 8.00D; System.out.println("x3均值:" + x3); double s1 = Math.sqrt(((6.125 - 8) * (6.125 - 8) + (6.125 - 4) * (6.125 - 4) + (6.125 - 5) * (6.125 - 5) + (6.125 - 6) * (6.125 - 6) + (6.125 - 7) * (6.125 - 7) + (6.125 - 8) * (6.125 - 8) + (6.125 - 6) * (6.125 - 6) + (6.125 - 5) * (6.125 - 5)) / 7.00D); System.out.println("s1方差:" + s1); double s2 = Math.sqrt(((5 - 6) * (5 - 6) + (5 - 2) * (5 - 2) + (5 - 7) * (5 - 7) + (5 - 5) * (5 - 5) + (5 - 3) * (5 - 3) + (5 - 7) * (5 - 7) + (5 - 4) * (5 - 4) + (5 - 6) * (5 - 6)) / 7.00D); System.out.println("s2方差:" + s2); double s3 = Math.sqrt(((5.25 - 5) * (5.25 - 5) + (5.25 - 7) * (5.25 - 7) + (5.25 - 6) * (5.25 - 6) + (5.25 - 3) * (5.25 - 3) + (5.25 - 4) * (5.25 - 4) + (5.25 - 7) * (5.25 - 7) + (5.25 - 5) * (5.25 - 5) + (5.25 - 5) * (5.25 - 5)) / 7.00D); System.out.println("s3方差:" + s3); double msb = (8 * (x1 - x) * (x1 - x) + 8 * (x2 - x) * (x2 - x) + 8 * (x3 - x) * (x3 - x)) / (3 - 1) * 1.00D; System.out.println("组间方差:" + msb); double mse = (((8 - x1) * (8 - x1) + (4 - x1) * (4 - x1) + (5 - x1) * (5 - x1) + (6 - x1) * (6 - x1) + (7 - x1) * (7 - x1) + (8 - x1) * (8 - x1) + (6 - x1) * (6 - x1) + (5 - x1) * (5 - x1)) + ((6 - x2) * (6 - x2) + (2 - x2) * (2 - x2) + (7 - x2) * (7 - x2) + (5 - x2) * (5 - x2) + (3 - x2) * (3 - x2) + (7 - x2) * (7 - x2) + (4 - x2) * (4 - x2) + (6 - x2) * (6 - x2)) + ((5 - x3) * (5 - x3) + (7 - x3) * (7 - x3) + (6 - x3) * (6 - x3) + (3 - x3) * (3 - x3) + (4 - x3) * (4 - x3) + (7 - x3) * (7 - x3) + (5 - x3) * (5 - x3) + (5 - x3) * (5 - x3))) / (24 - 3) * 1.00D; System.out.println("组内方差:" + mse); double f=msb/mse; System.out.println("F统计量:" + f); }
参考:
https://www.cnblogs.com/ljhdo/p/10818526.html?ivk_sa=1024320u





