Bell-Ford算法找最短路径

Dijkstras算法不能够处理图中的负权重的路径，而Bell-Ford则弥补了这一缺点。时间复杂度为|V|*|E|。

Bell-Ford的思想是每次遍历图中的边，并松弛该条边。假设S到V的最短路径是S-V1-V2-V3...-V，则第一次遍历完成时，S-V1边肯定会被松弛，并且V1肯定是这条最短路径上的点，这样，当|V|-1次遍历完成时，Vn-1 - V这条边肯定会被松弛，并找到V（假设这是离源点最远的点）。

 伪代码描述：

 

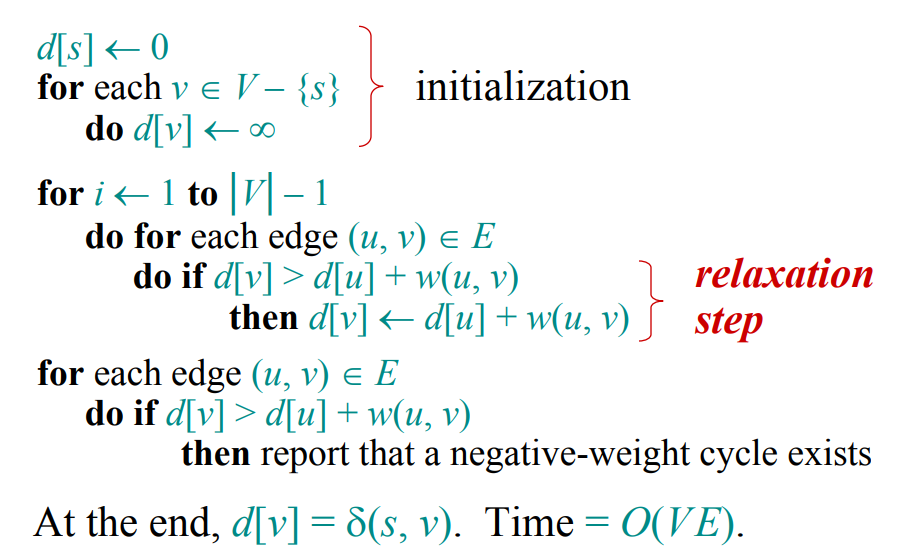
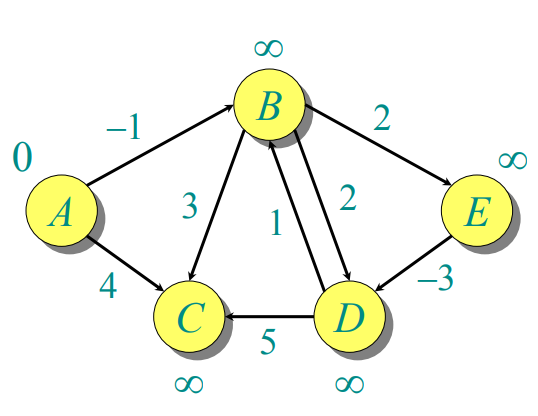
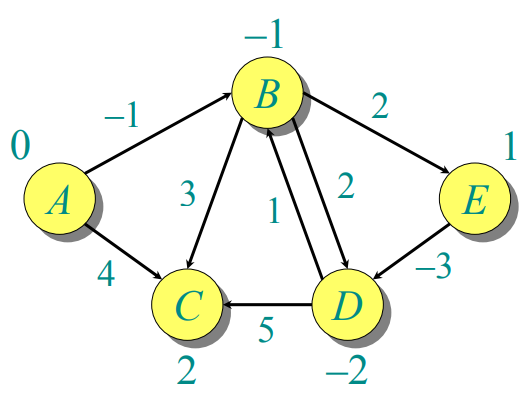
public class BellmanFord2 {
    
    public static void main(String[] args) {
        
        int[][] graph= {{0,-1,4,999,999},
                        {999,0,3,2,2},
                        {999,999,0,999,999},
                        {999,1,5,0,999},
                        {999,999,999,-3,0}};
        String arr[]= {"A","B","C","D","E"};
        Node[] d=getShortestPath(graph,arr,0);
        Node dest=d[3];
        System.out.print(d[3].value);
        int i=1;
        while(dest.pointTo!=null) {
            System.out.print(dest.pointTo.value+" ");
            dest=dest.pointTo;
            
        }
        
    }
    
    public static Node[] getShortestPath(int[][] graph,String[] arr,int s) {
        Node root=null;
        Node[] d=new Node[arr.length];
        //初始化，将所有顶点装入d数组中，并令其权值最大（999）
        for(int i=0;i<graph.length;i++) {
            d[i]=new Node();
            d[i].key=i;
            d[i].value=arr[i];
            d[i].weight=999;
            d[i].flag=false;
            d[i].pointTo=null;
        }
        //根据邻接矩阵建立边数组
        List<Edge> edges=new ArrayList<>();
        for(int i=0;i<graph.length;i++) {
            for(int j=0;j<graph.length;j++) {
                if(graph[i][j]<999&&(i!=j)) {
                    Edge e=new Edge();
                    e.begin=i;
                    e.end=j;
                    e.weight=graph[i][j];
                    edges.add(e);
                    
                }
            }
        }
        root=d[s];
        root.flag=true;
        root.weight=0;
        //每次遍历所有的边并松弛，一共便利|V|-1次
        for(int i=1;i<graph.length-1;i++) {
            for(int j=0;j<edges.size();j++) {
                if(d[edges.get(j).end].weight>d[edges.get(j).begin].weight+edges.get(j).weight) {
                    d[edges.get(j).end].weight=d[edges.get(j).begin].weight+edges.get(j).weight;
                    d[edges.get(j).end].pointTo=d[edges.get(j).begin];
                }
            }
        }
        //若第|V|次遍历时，边还能被松弛，说明存在负回路。此时不存在最短路径
        for(int j=0;j<edges.size();j++) {
            if(d[edges.get(j).end].weight>d[edges.get(j).begin].weight+edges.get(j).weight) {
                throw new RuntimeException("存在负回路，没有最短距离!!!");
            }
        }
        return d;
    }
    
}
//边的类
class Edge{
    int begin;
    int end;
    int weight;
}

class Node{
    String value;
    Node pointTo;
    int weight;
    int key;
    boolean flag=true;
}

打印结果