算法导论Dijkstra算法

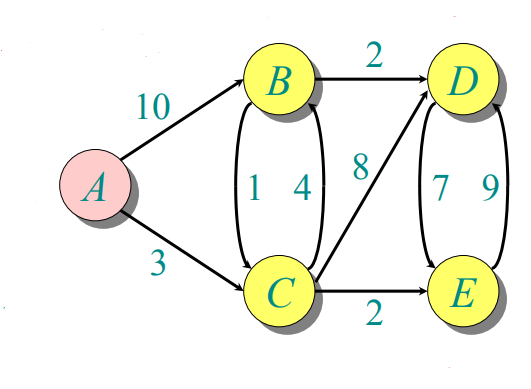
Dijkstra的思想和MST的思想很相似，都是用两个集合来装已经确定最小的顶点和还未确定是否是最小的顶点。但是MST是每次从集合V-A中找距离集合A最近的顶点，并把它放入A中。而Dijkstra是找V-A中距离源点（s）最近的点，其中采用了松弛操作，即 s->v的距离>s->u+u->v的距离，其中v为还未确定的点，u为已确定点。

import java.util.ArrayList;

public class Dijkstra {
    
        public ArrayList<Node> getPaths(int[][] graph,String[] arr,String dest) {
            Node root=null;
            
            Node[] d=new Node[graph.length];
            ArrayList<Node> a=new ArrayList<>();
            for(int i=0;i<d.length;i++) {
                d[i]=new Node();
                d[i].weight=999;
                d[i].value=arr[i];
                d[i].key=i;
            }
            int s=0;
            Node u=d[s];
            root=d[s];
            root.weight=0;
            root.flag=false;
            a.add(root);
            //当集合A中的顶点个数与V中一样时，表示已经处理完所有的顶点
            while(a.size()<graph.length) {
                for(int i=0;i<graph.length;i++) {
                    //松弛操作
                    if(d[i].weight>u.weight+graph[u.key][i]) {
                        d[i].weight=u.weight+graph[u.key][i];
                        d[i].pointTo=u;
                    }
                }
                u=getMin(d);
                a.add(u);
            }
            ArrayList<Node> path=new ArrayList<>();
            Node x=null;
            //寻找参数表示的终点
            for(int i=0;i<a.size();i++) {
                if(a.get(i).value.equals(dest)) {
                    x=a.get(i);
                    break;
                }
            }
            if(x!=null) {
                //从终点开始往前找经过的点
                while(x.pointTo!=null) {
                    path.add(x);
                    x=x.pointTo;
                }
            }
            else {
                throw new RuntimeException("x为空！");
            }
            return path;
        }
        public Node getMin(Node[] v) {
            int min=1000;
            int minIndex=-1;
            for(int i=0;i<v.length;i++) {
                //flag为false表示该顶点已经确定过了，不参比较
                if(v[i].weight<min&&v[i].flag) {
                    min=v[i].weight;
                    minIndex=i;
                }
            }
            //找到最小的顶点加入A，该顶点已经确定，以后不参与比较
            v[minIndex].flag=false;
            return v[minIndex];
        }
}

顶点类

class Node{
    String value;
    Node pointTo;
    int weight;
    int key;
    boolean flag=true;
}

测试类

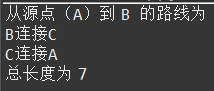
public class Test {
    public static void main(String[] args) throws Exception, SecurityException {
        String[] arr= {"A","B","C","D","E"};
        int[][] graph= {{0,10,3,999,999},
                        {999,0,1,2,999},
                        {999,4,0,8,2},
                        {999,999,999,0,7},
                        {999,999,999,9,0},
                        };
        Dijkstra dijk=new Dijkstra();
        String dest="B";
        ArrayList<Node> node=dijk.getPaths(graph, arr,dest);
        System.out.println("从源点（A）到 "+dest+" 的路线为");
        for(int i=0;i<node.size();i++) {
            System.out.println(node.get(i).value+"连接"+node.get(i).pointTo.value);
            
        }
        System.out.print("总长度为 "+node.get(0).weight);
        
    }
}

 

运算结果