模拟退火_matlab
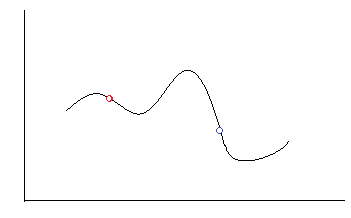
退火是一种金属热处理工艺,指的是将金属缓慢加热到一定温度,保持足够时间,然后以适宜速度冷却。在温度较高时,固体内部的粒子热运动较为激烈,随着温度的降低,固体内能减少,粒子的运动也渐渐减缓。这个过程和我们求函数最小值有什么共同点呢,看下面这个图,如果初始点在红色位置,按照梯度搜索,是不可能找到全局最小值的。但是模仿退火过程,如果下一步的位置对应的值更小,就保存下来,如果变大了,以一定的概率来选择是不是保留。在温度很高的时候,这个概率是比较大的,这就能够实现跳出局部最优,而随着温度越来越低,这个概率会变低,而且温度也不是匀速降低的,而是以一个越来越慢的速度降低,这就保证了在全局最优附近能够搜索得更仔细。
下面给出两个很经典的例子:
1.商旅问题
2.0-1背包问题
1.商旅问题:一个商人要从自己的国家出发去n个国家走一遍售卖商品,最终回到自己的国家。问他应该如何规划自己访问国家的顺序,才能走最少的路程呢?
解题思路:一开始看到这个问题,可能会想到前面学过的Floyed或者Dijkstra算法,但是他们都是计算两点之间最短路问题的,而不是吧所有的点全走一遍。所以就不能用了。面对这样的组合规划问题,模拟退火就能派上用场了。
(1)设置模拟退火初参数
(2)随机生成一个访问序列[1,2,3...n],记作sol
(3)在当前温度高于终温情况下循环,生成对sol的扰动,形式是随机的两个国家顺序互换或者三个国家之间的国家位置互换
(4)计算新的sol的距离,如果距离比sol_best(最好的顺序)对应的距离e_best(最短的距离)还小,那么更新sol_best和e_best,如果不是,则按一定几率接受这个顺序,把他当做新的顺序进行下一次循环
(5)当温度达到终温是跳出循环,出书结果和访问顺序
clear; clc; b=0.99; t0=97; tf=3; t=t0; Markov_length=100; a=[1 3 2; 2 0 0; 3 5 5 4 3 1]; a(:,1) =[]; amount=size(a,1) dist_matrix=zeros(amount,amount); disp(dist_matrix); plot(a(:,1),a(:,2),'*'); coor_x_tmp1=a(:,1)*ones(1,amount); disp(coor_x_tmp1); coor_x_tmp2=coor_x_tmp1'; disp(coor_x_tmp2); coor_y_tmp1=a(:,2)*ones(1,amount); coor_y_tmp2=coor_y_tmp1'; dist_matrix=sqrt((coor_x_tmp1-coor_x_tmp2).^2+(coor_y_tmp1-coor_y_tmp2).^2); disp(dist_matrix); sol_new=1:amount; e_current=inf; e_best=inf; sol_current=sol_new; sol_best=sol_new; p=1; while t>tf for r=1:Markov_length if rand<0.5 ind1=0; ind2=0; while ind1==ind2 ind1=ceil(rand.*amount); ind2=ceil(rand.*amount); end tmp1=sol_new(ind1); sol_new(ind1)=sol_new(ind2); sol_new(ind2)=tmp1; else ind1=0;ind2=0;ind3=0; while(ind1==ind2)||(ind1==ind3)||(ind2==ind3)||(abs(ind1-ind2)==1) ind1=ceil(rand.*amount); ind2=ceil(rand.*amount); ind3=ceil(rand.*amount); end arr=[ind1 ind2 ind3] for i=1:3 for j=1:2 if arr(j)>arr(j+1) tmp=arr(j); arr(j)=arr(j+1); arr(j+1)=tmp; end end end ind1=arr(1);ind2=arr(2);ind3=arr(3); tmplist1=sol_new((ind1+1):(ind2-1)); sol_new((ind1+1):(ind1+ind3-ind2+1))=sol_new((ind2):ind3); sol_new((ind1+ind3-ind2+2):ind3)=tmplist1; end e_new=0; for i=1:(amount-1) e_new=e_new+dist_matrix(sol_new(i),sol_new(i+1)); end e_new=e_new+dist_matrix(sol_new(amount),sol_new(1)); if e_new<e_current e_current=e_new; sol_current=sol_new; if e_new<e_best e_best=e_new; sol_best=sol_new; end else if rand<exp(-(e_new-e_current)./t) e_current=e_new; sol_current=sol_new; else sol_new=sol_current; end end end t=t.*b; end disp(sol_best);


 浙公网安备 33010602011771号
浙公网安备 33010602011771号