堆中的路径 java描述

将一系列给定数字插入一个初始为空的小顶堆H[]。随后对任意给定的下标i，打印从H[i]到根结点的路径。

输入格式:

每组测试第1行包含2个正整数N和M(≤1000)，分别是插入元素的个数、以及需要打印的路径条数。下一行给出区间[-10000, 10000]内的N个要被插入一个初始为空的小顶堆的整数。最后一行给出M个下标。

输出格式:

对输入中给出的每个下标i，在一行中输出从H[i]到根结点的路径上的数据。数字间以1个空格分隔，行末不得有多余空格。

输入样例:

5 3
46 23 26 24 10
5 4 3

输出样例:

24 23 10
46 23 10
26 10

思路：堆是一个完全二叉树，用数组来存放堆中数据，角标为1代表堆顶。若当前角标为i,左儿子为2i，右儿子为2i+1，父节点为i/2。

 　　  每插入一个元素，把他放在完全二叉树最后一个位置，使其与父节点比较，若小于父节点，父节点值和插入元素互换，继续循

          环比较，因为设置了哨兵arr[0]=-10001， 所以插入的数据角标最小只可能为1，不可能为0.

import java.util.Scanner;
//声明一个堆类
class heap 
{
    //堆中数据内容有一个数组和一个表示堆大小的size
    int[] arr;
    int size;
    //初始化堆，因为N取值是-10000到10000，取10001是为了数组能满足题目要求，arr[0]=-10001作为哨兵，使数组从角标为1开始存放数据
    //一开始堆是空的，所以size=0
    public heap()
    {
        arr=new int[10001];
        arr[0]=-10001;
        size=0;
    }
    //向堆中插入数据，堆的数据结构是一个完全二叉树
    public void insert(int num)
    {
        if (size==0)
        {
            arr[1]=num;
            size++;
        }
        else
        {
            arr[++size]=num;
            //恢复t
            int t=size;
            while (num<arr[t/2])
            {
                int temp=arr[t/2];
                arr[t/2]=num;
                arr[t]=temp;
                t=t/2;
            }        
        }
    }
    //取得从给定角标到堆顶的路径
    public void road(int num)
    {
        while (num!=0)
        {
            System.out.print(arr[num]+" ");
            num=num/2;
        }
        if (num==0)
        {
            System.out.println();
        }
    }
}
//测试类
class test
{
    public static void main(String[] args) 
    {
        Scanner sc=new Scanner(System.in);
        heap h=new heap();
        int N=sc.nextInt();
        int M=sc.nextInt();
        for (int i=0;i<N ;i++ )
        {
            int num=sc.nextInt();
            h.insert(num);
        }
        
        for (int i=0;i<M ;i++ )
        {
            int r=sc.nextInt();
            h.road(r);
        }
    }
}

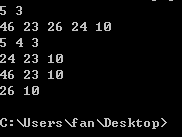
打印结果：