matlab实现又向图与无向图的最短路径

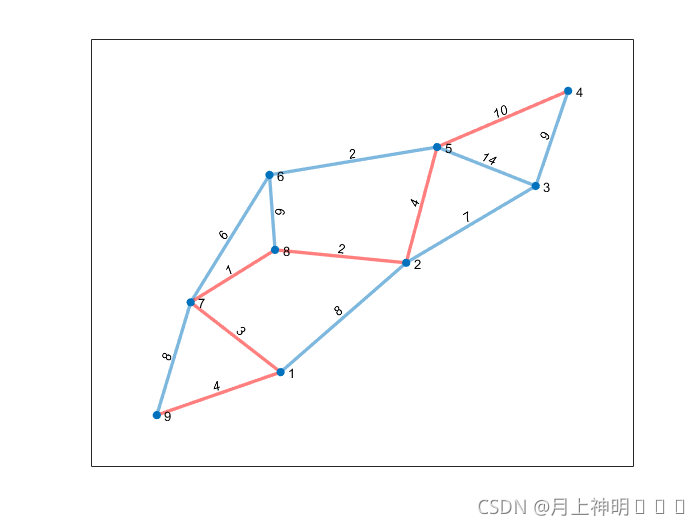
无向图的最短路径

s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4];
t = [1 7 7 2 8 3 5 8 6 8 5 3 4 3 ];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];%权重
G = graph(s,t,w);%生成稀疏矩阵
plot(G,'EdgeLabel',G.Edges.Weight,'LineWidth',2);
[P,D] = shortestpath(G,9,4);
%%高亮显示路径
myplot = plot(G,'EdgeLabel',G.Edges.Weight,'LineWidth',2);
highlight(myplot,P,'EdgeColor','r');

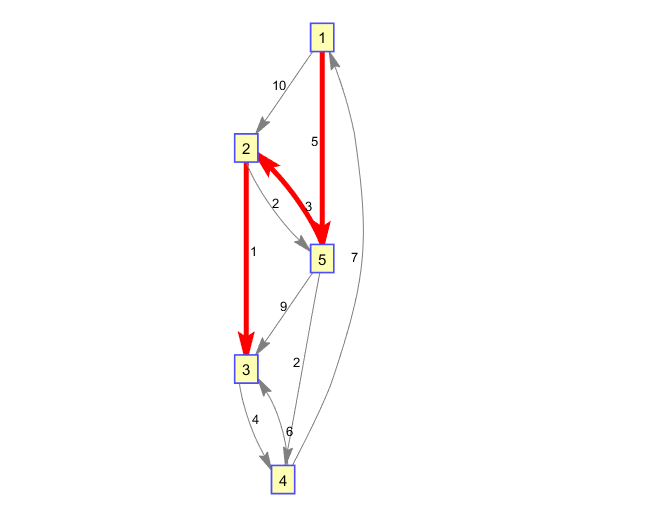
有向图的最短路径

clc,clear
w = [10,5,2,1,4,6,7,3,9,2];
DG = sparse([1,1,2,2,3,4,4,5,5,5],[2,5,5,3,4,3,1,2,3,4],w);
[dist,path,pred] = graphshortestpath(DG,1,3)
% biograph生成图对象，view显示该图
point_name = ['1','2','3','4','5'];
h = view(biograph(DG,point_name,'ShowWeights','on'))
% 将最短路径的节点和边缘标记为红色并增加线宽
% getedgesbynodeid得到图h的指定边的句柄
% 第一个参数是图，第二个是边的出点，第三个是边的入点
% 句柄确保能找到对应的东西
% get查询图的属性，h.Nodes(path)，‘ID’得到图中最短路径
% set函数设置图形属性
edges = getedgesbynodeid(h,get(h.Nodes(path),'ID'));
set(edges,'LineColor',[1 0 0])
set(edges,'LineWidth',3)

matlab实现迪杰斯特拉算法

参数	含义
indx	是否判断该店是否已经被包含
dis	距离起点的最短距离
parent	该结点的父上一节点

1.将结点1定为初始结点
2.将结点1的距离赋值为0，即dis(1) = 0
3.循环所有结点
4.将现在的结点pre赋值为已走过，即indx(pre) = 1
5.循环该行的每一列
6.将每一列的结点的距离与现有节点的距离做判断，如果小则替换，并更新父节点
7.根据最短距离更新pre结点

% 最短路径
s = [1,1,2,2,3,4,4,4,5];
t = [2,3,3,4,5,3,5,6,6];
w = [1,12,9,3,5,4,13,15,4];
G = digraph(s,t,w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2);
gra = [0,1,12,inf,inf,inf;
    inf,0,9,3,inf,inf;
    inf,inf,0,inf,5,inf;
    inf,inf,4,0,13,15;
    inf,inf,inf,inf,0,4;
    inf,inf,inf,inf,inf,0];
indx = zeros(1,6); %是否已经走过
pre = 1;
dis = Inf(1,6); %距离起点的最短距离
dis(1) = 0;
parent = zeros(1,6); %父元素
[w,h] = size(gra)
for i=1:h
    indx(pre) = 1;
    for j=1:w
        if(gra(pre,j)~=inf&&gra(pre,j)~=0&&indx(j)==0)
            if(dis(j)>(gra(pre,j)+dis(pre)))
                dis(j) = gra(pre,j)+dis(pre);
                parent(j) = pre;
            end
        end
    end
    ddd = inf;
    for z=1:w
        if(indx(z)==0&&gra(i,z)<ddd)
            ddd = gra(i,z);
            pre = z;
        end
    end
end