2717. 半有序排列

给你一个下标从 0 开始、长度为 n 的整数排列 nums 。

如果排列的第一个数字等于 1 且最后一个数字等于 n ，则称其为 半有序排列 。你可以执行多次下述操作，直到将 nums 变成一个 半有序排列 ：

选择 nums 中相邻的两个元素，然后交换它们。
返回使 nums 变成 半有序排列 所需的最小操作次数。

排列 是一个长度为 n 的整数序列，其中包含从 1 到 n 的每个数字恰好一次。

示例 1：

输入：nums = [2,1,4,3]
输出：2
解释：可以依次执行下述操作得到半有序排列：
1 - 交换下标 0 和下标 1 对应元素。排列变为 [1,2,4,3] 。
2 - 交换下标 2 和下标 3 对应元素。排列变为 [1,2,3,4] 。
可以证明，要让 nums 成为半有序排列，不存在执行操作少于 2 次的方案。
示例 2：

输入：nums = [2,4,1,3]
输出：3
解释：
可以依次执行下述操作得到半有序排列：
1 - 交换下标 1 和下标 2 对应元素。排列变为 [2,1,4,3] 。
2 - 交换下标 0 和下标 1 对应元素。排列变为 [1,2,4,3] 。
3 - 交换下标 2 和下标 3 对应元素。排列变为 [1,2,3,4] 。
可以证明，要让 nums 成为半有序排列，不存在执行操作少于 3 次的方案。
示例 3：

输入：nums = [1,3,4,2,5]
输出：0
解释：这个排列已经是一个半有序排列，无需执行任何操作。

提示：

2 <= nums.length == n <= 50
1 <= nums[i] <= 50
nums 是一个 排列

解题思路：
1.初始化变量：获取数组长度 n，并初始化两个变量 index1 和 index2 分别用于存储数组中值为 1 和 n 的索引。
2.遍历数组：通过一个 for 循环遍历数组，找到值为 1 和 n 的元素的索引。
3.计算结果：根据 index1 和 index2 的相对位置，计算并返回一个整数值 res。

详细解释
1.初始化变量：
n：数组的长度。
index1 和 index2：分别初始化为 -1，用于存储值为 1 和 n 的索引。
2.遍历数组：
使用 for 循环遍历数组 nums。
在每次迭代中，检查当前元素是否为 1 或 n，并相应地更新 index1 和 index2。
3.计算结果：
根据 index1 和 index2 的相对位置，计算结果 res。
如果 index1 大于 index2，则 res 等于 index1 + (n - index2 - 2)。
否则，res 等于 index1 + (n - index2 - 1)。
4.返回结果：
返回计算得到的 res 值。

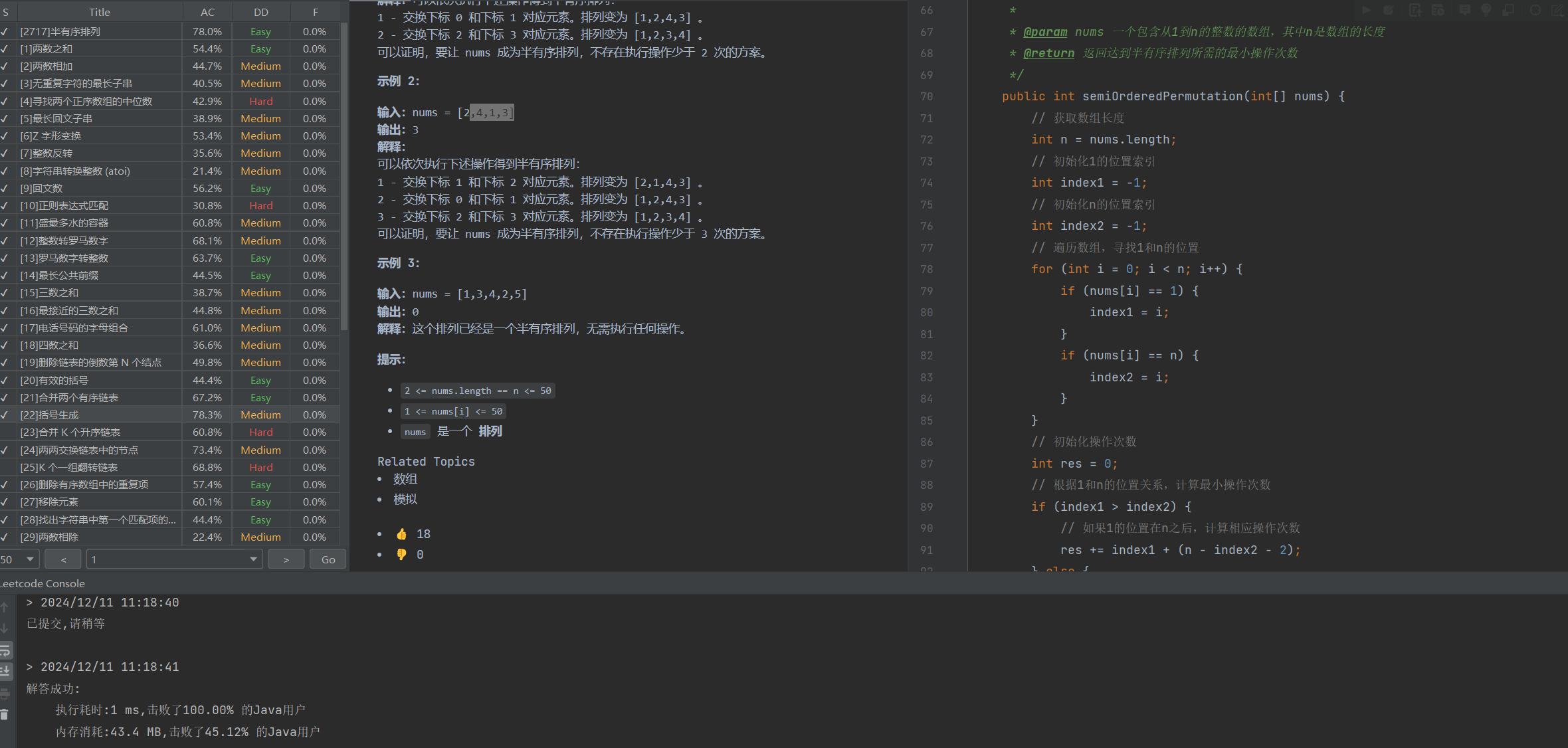
完整代码：

class Solution {
    /**
     * 计算半有序排列的最小操作次数
     * 半有序排列定义为数组中1和n（数组长度）的位置满足一定条件的排列
     * 此函数旨在通过最少的操作次数将数组转换为半有序排列
     * 操作定义为：选择任意两个元素并交换它们的位置
     *
     * @param nums 一个包含从1到n的整数的数组，其中n是数组的长度
     * @return 返回达到半有序排列所需的最小操作次数
     */
    public int semiOrderedPermutation(int[] nums) {
        // 获取数组长度
        int n = nums.length;
        // 初始化1的位置索引
        int index1 = -1;
        // 初始化n的位置索引
        int index2 = -1;
        // 遍历数组，寻找1和n的位置
        for (int i = 0; i < n; i++) {
            if (nums[i] == 1) {
                index1 = i;
            }
            if (nums[i] == n) {
                index2 = i;
            }
        }
        // 初始化操作次数
        int res = 0;
        // 根据1和n的位置关系，计算最小操作次数
        if (index1 > index2) {
            // 如果1的位置在n之后，计算相应操作次数
            res += index1 + (n - index2 - 2);
        } else {
            // 如果1的位置在n之前，计算相应操作次数
            res += index1 + (n - index2 - 1);
        }
        // 返回操作次数
        return res;
    }
  }