910. 最小差值 II

给你一个整数数组 nums，和一个整数 k 。

对于每个下标 i（0 <= i < nums.length），将 nums[i] 变成 nums[i] + k 或 nums[i] - k 。

nums 的 分数 是 nums 中最大元素和最小元素的差值。

在更改每个下标对应的值之后，返回 nums 的最小 分数 。

示例 1：

输入：nums = [1], k = 0
输出：0
解释：分数 = max(nums) - min(nums) = 1 - 1 = 0 。
示例 2：

输入：nums = [0,10], k = 2
输出：6
解释：将数组变为 [2, 8] 。分数 = max(nums) - min(nums) = 8 - 2 = 6 。
示例 3：

输入：nums = [1,3,6], k = 3
输出：3
解释：将数组变为 [4, 6, 3] 。分数 = max(nums) - min(nums) = 6 - 3 = 3 。

提示：

1 <= nums.length <= 104
0 <= nums[i] <= 104
0 <= k <= 104

解题思路：
1.排序：首先对数组 nums 进行排序。
2.初始化变量：
n：数组长度。
min：排序后数组的最小值。
max：排序后数组的最大值。
ans：初始答案为 max - min。
3.遍历数组：
遍历数组的每个元素（除最后一个），计算当前元素 left 和下一个元素 right。
如果 left 大于等于 min 且 right 小于等于 max，则更新 ans 为 Math.min(ans, Math.max(max - k, nums[i]+k) - Math.min(min+k, right-k))。
返回结果：最终返回 ans。

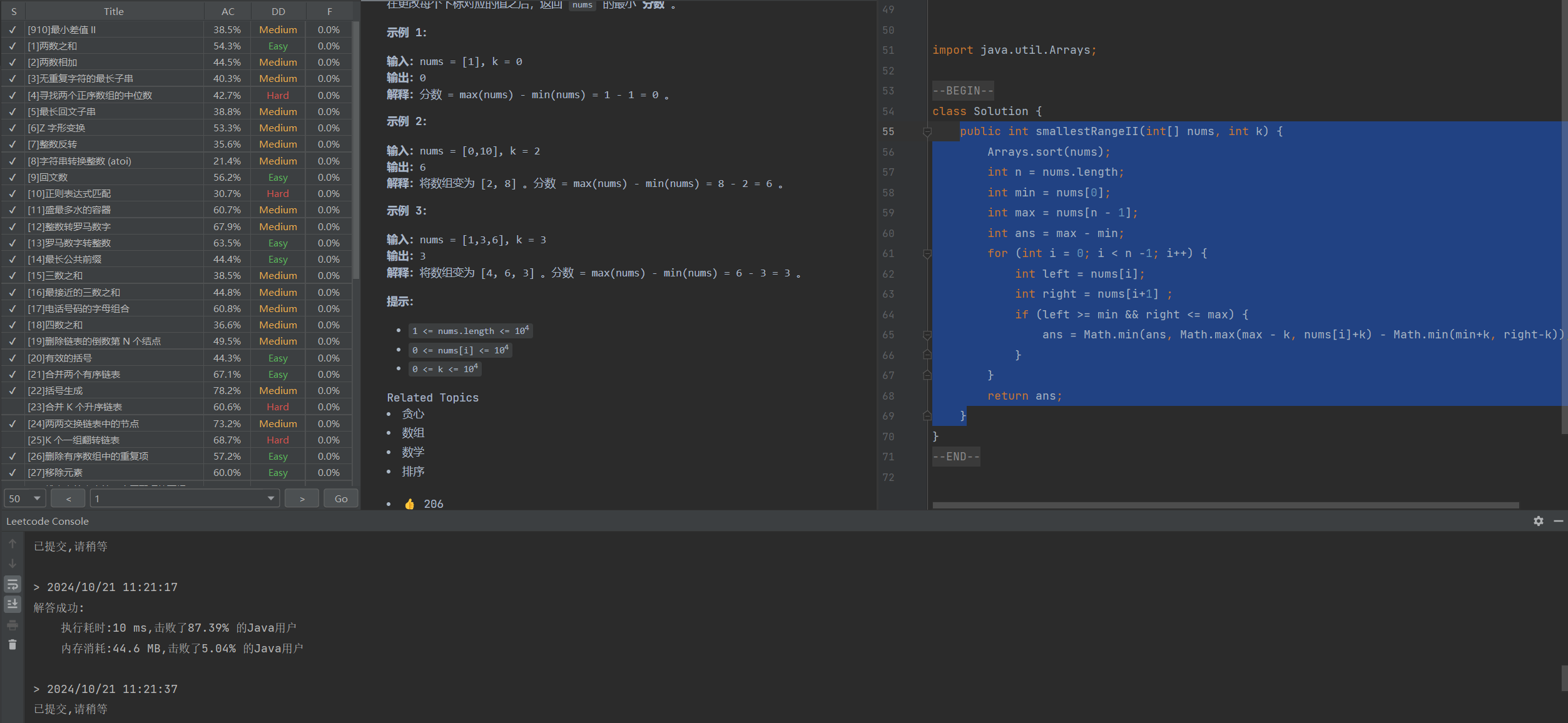
 完整代码：
    /**
     * 计算数组在进行最多k的增减操作后可能的最小范围
     * 
     * @param nums 原始整数数组
     * @param k 可以对数组元素进行增减的最大值
     * @return 返回调整后数组可能的最小范围
     */
    public int smallestRangeII(int[] nums, int k) {
        // 对数组进行排序，以便后续处理
        Arrays.sort(nums);
        int n = nums.length;
        // 初始化最小值和最大值为数组的首尾元素
        int min = nums[0];
        int max = nums[n - 1];
        // 初始化答案为当前最大值与最小值的差
        int ans = max - min;
        // 遍历数组，寻找可能的最小范围
        for (int i = 0; i < n - 1; i++) {
            int left = nums[i];
            int right = nums[i + 1];
            // 检查当前左右值是否在全局最小值和最大值范围内
            if (left >= min && right <= max) {
                // 更新答案为当前最小范围
                ans = Math.min(ans, Math.max(max - k, nums[i] + k) - Math.min(min + k, right - k));
            }
        }
        // 返回可能的最小范围
        return ans;
    }