2376.统计特殊整数
如果一个正整数每一个数位都是 互不相同 的,我们称它是 特殊整数 。
给你一个 正 整数 n ,请你返回区间 [1, n] 之间特殊整数的数目。
示例 1:
输入:n = 20
输出:19
解释:1 到 20 之间所有整数除了 11 以外都是特殊整数。所以总共有 19 个特殊整数。
示例 2:
输入:n = 5
输出:5
解释:1 到 5 所有整数都是特殊整数。
示例 3:
输入:n = 135
输出:110
解释:从 1 到 135 总共有 110 个整数是特殊整数。
不特殊的部分数字为:22 ,114 和 131 。
解题思路:
思路一:
1.使用位运算
实现思路
1.初始化位图:使用一个整数 bitmap 作为位图,每一位代表一个数字是否存在。
2.遍历数字的每一位:每次取出数字的最后一位,并检查该位是否已经在位图中被设置过。
3.设置位图:如果该位未被设置,则将其设置为 1。
4.返回结果:如果整个数字遍历完成后没有重复的数字,则返回 true;否则返回 false。
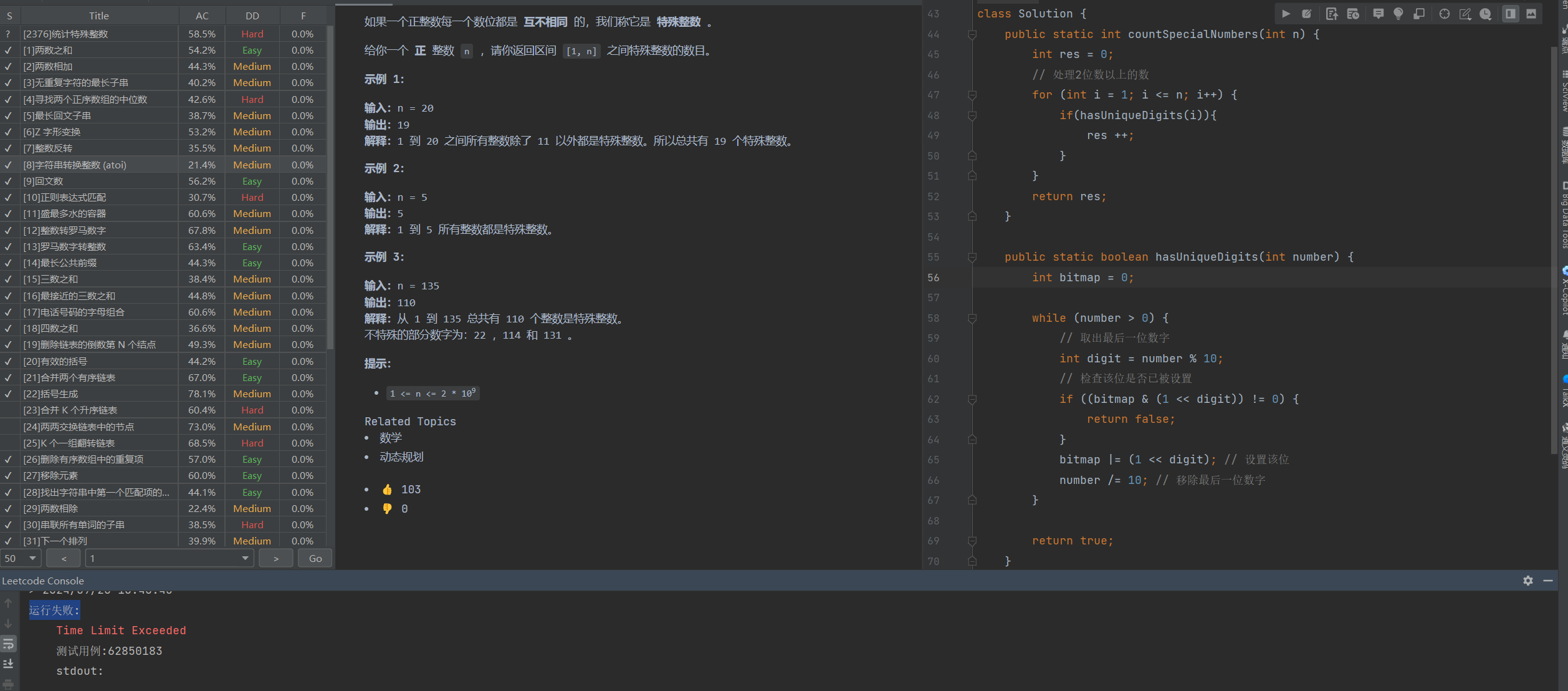
该思路提交还是超时了,那如何解决超时的问题呢?
上述代码虽然使用了位图来减少内存的使用,但是时间复杂度还是未能解决?如果我们从数字的本身出发那么只需要关注每个数字位置不重复就可以了,具体的思路为:
1.将输入整数n转换为字符串s,初始化结果变量ans、排列数变量permutations。
2.计算小于s长度的所有位数的非重复数字组合总数。
3.遍历s中的每个字符,计算相同位数中不大于当前数字的非重复组合数,并累加到ans。
4.判断是否所有数字均不重复,若是,则结果ans加一。
5.返回最终结果ans。
步骤分解:
1.先把整数转换成字符串
String s = Integer.toString(n);
2.计算所有位数小于s的非重复数字组合的总数,并累加到ans中
int ans = 0;
int permutations = 1;
//遍历字符串s从第2个字符到最后一个字符
for (int i = 1; i < s.length(); i++) {
ans += 9 * permutations;
permutations *= 10 - i;
}
这里解释下这段代码的含义:
permutations 表示的是在当前位置可以选取的不同数字的数量。对于每一位,可选的数字数量会根据位的位置变化。
对于第一位(十位),可以选择 1 到 9 中的任意一个数字(不能选择 0),因此有 9 种选择。
对于第二位(个位),可以选择剩下的 0 到 9 中的 9 个数字(排除已经选择的那一个数字),因此有 9 种选择。
对于第三位,可以选择剩下的 8 个数字,以此类推。
因此,在两位数的情况下,permutations 的初始值为 9(第一位的选择),然后乘以 9(第二位的选择),得到 81 种组合。每次循环中,permutations 会被更新为下一个位置的可选数字数量。
具体来说:
第一位:9 种选择。
第二位:9 种选择。
所以 permutations 在两位数情况下始终为 9
3.该函数计算字符串s中不同数字组合的数量。主要步骤如下:
int set = 0;
for (int i = 0; i < s.length(); i++) {
// 转换为数字
int num = s.charAt(i) - '0';
// 该行代码生成一个位掩码。具体功能如下:
// 1 << num:将1左移num位,得到一个二进制数,该二进制数的最高位为1,其余为0。
// (1 << num) - 1:将上述结果减1,得到一个二进制数,该数的前num位全为1。例如,若num为3,则结果为0b11
int mask = (1 << num) - 1;
// 该表达式计算(set & mask) ^ mask的结果中的二进制位1的数量。 具体步骤如下:
// set & mask:对set和mask进行按位与操作。
// (set & mask) ^ mask:将上一步结果与mask进行按位异或操作。
// Integer.bitCount(...):计算第2步结果中二进制位1的数量。
int count = Integer.bitCount((set & mask) ^ mask);
if (i == 0) {
count--;
}
// 这段代码将 count 与 permutations 的乘积累加到 ans 中。具体功能如下:
// 将 count 与 permutations 相乘。
//将乘积结果累加到变量 ans 中。这通常用于计算某种组合或排列的总数
ans += count * permutations;
if ((set & (1 << num)) != 0) {
break;
}
permutations /= 10 - (i + 1);
set |= 1 << num;
}
if (Integer.bitCount(set) == s.length()) {
ans++;
}
return ans;
代码整体思路:
1.初始化变量set为0。
2.遍历字符串s中的每个字符,将其转换为数字,并计算掩码mask。
3.使用位运算统计当前数字在已处理子串中的出现次数count。
4.如果是第一个字符,则count减1。
5.更新答案ans。
6.检查数字是否重复,若重复则提前结束循环。
7.更新排列数permutations。
8.将当前数字加入已处理集合set。
9.最后检查所有数字是否唯一,若是,则ans加1。
10.最终返回结果ans
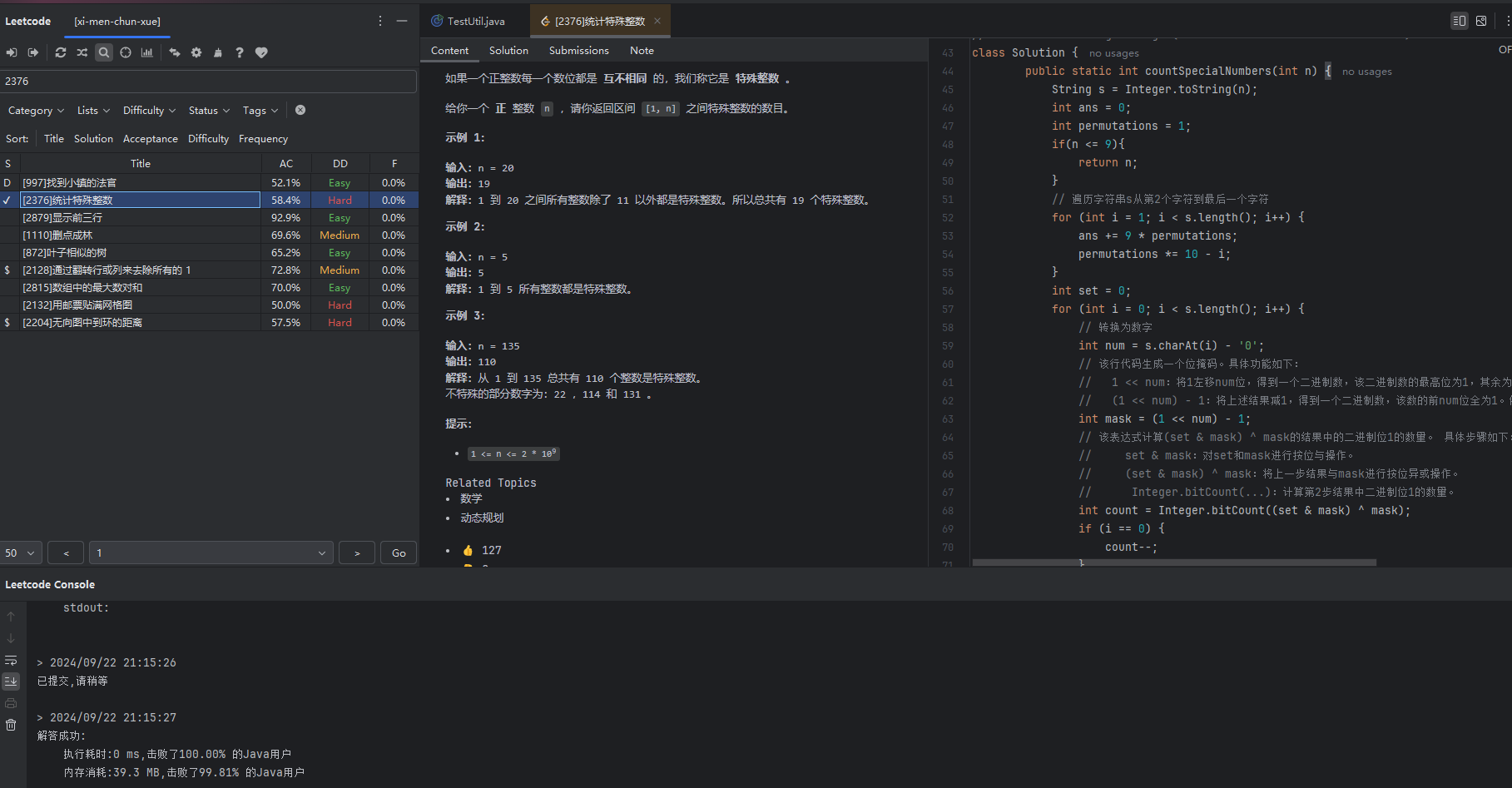
整体代码:
class Solution {
public static int countSpecialNumbers(int n) {
String s = Integer.toString(n);
int ans = 0;
int permutations = 1;
if(n <= 9){
return n;
}
// 遍历字符串s从第2个字符到最后一个字符
for (int i = 1; i < s.length(); i++) {
ans += 9 * permutations;
permutations *= 10 - i;
}
int set = 0;
for (int i = 0; i < s.length(); i++) {
// 转换为数字
int num = s.charAt(i) - '0';
// 该行代码生成一个位掩码。具体功能如下:
// 1 << num:将1左移num位,得到一个二进制数,该二进制数的最高位为1,其余为0。
// (1 << num) - 1:将上述结果减1,得到一个二进制数,该数的前num位全为1。例如,如果num为3,则 mask 的值为二进制 0111
int mask = (1 << num) - 1;
// 该表达式计算(set & mask) ^ mask的结果中的二进制位1的数量。 具体步骤如下:
// set & mask:对set和mask进行按位与操作。
// (set & mask) ^ mask:将上一步结果与mask进行按位异或操作。
// Integer.bitCount(...):计算第2步结果中二进制位1的数量。
int count = Integer.bitCount((set & mask) ^ mask);
if (i == 0) {
count--;
}
// 这段代码将 count 与 permutations 的乘积累加到 ans 中。具体功能如下:
// 将 count 与 permutations 相乘。
//将乘积结果累加到变量 ans 中。这通常用于计算某种组合或排列的总数
ans += count * permutations;
if ((set & (1 << num)) != 0) {
break;
}
permutations /= 10 - (i + 1);
set |= 1 << num;
}
if (Integer.bitCount(set) == s.length()) {
ans++;
}
return ans;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号