AOJ 0531 坐标离散化
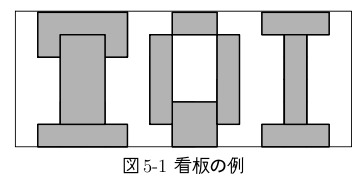
涂色:(日文题目,自己翻译成了中文)为了宣传信息竞赛,要在长方形的三合板上喷油漆来制作招牌。三合板上不需要涂色的部分预先贴好了护板。被护板隔开的区域要涂上不同的颜色,比如上图就应该涂上5种颜色。请编写一个程序计算涂色数量,输入数据中,保证看板不会被护板全部遮住,并且护板的边一定是水平或垂直的。
输入:
第一个数是宽w(1 ≤ w ≤ 1000000),第二个数是高h(1 ≤ h ≤ 1000000)。
第二行是护板的数量n(1 ≤ n ≤ 1000),接着n行是每个护板的左下角坐标 (x1 , y1 )和右上角坐标 (x2 , y2 ),用空格隔开: x1 , y1 , x2 , y2 (0 ≤ x1< x2 ≤ w, 0 ≤ y1 < y2 ≤ h 都是整数)
招牌的坐标系如下,左下角是 (0, 0) ,右上角是(w, h) , 测试集中的30%都满足w ≤ 100, h ≤ 100, n ≤ 100。

输出:
一个整数,代表涂色数量。
输入例
15 6 10 1 4 5 6 2 1 4 5 1 0 5 1 6 1 7 5 7 5 9 6 7 0 9 2 9 1 10 5 11 0 14 1 12 1 13 5 11 5 14 6 0 0
输出例子
5
思路
使用坐标离散化求解,坐标离散化的思想是:当坐标范围很大而坐标数量很少时,可以考虑把所有用到的横坐标排序,然后用每个坐标对应的下标来更新坐标位置。
挡板有面积,可以压缩到很苗条的1*n,空白部分也需要压缩,在网上查找到了利用imos法高效地统计方法。
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
int N,H,W;
int X1[1000],X2[1000],Y1[1000],Y2[1000];
int fld[2002][2002],dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};
int compress(int *x1,int *x2,int w){
vector<int>xs;
for(int i=0;i<N;i++){
int tx1=x1[i],tx2=x2[i];
if(1<=tx1 && tx1<w)xs.push_back(tx1);
if(1<=tx2 && tx2<w)xs.push_back(tx2);
}
xs.push_back(0);
xs.push_back(w);
sort(xs.begin(),xs.end());
xs.erase(unique(xs.begin(),xs.end()),xs.end());
for(int i=0;i<N;i++){
x1[i]=find(xs.begin(),xs.end(),x1[i])-xs.begin();
x2[i]=find(xs.begin(),xs.end(),x2[i])-xs.begin();
}
return xs.size()-1;
}
int bfs(void){
int ans=0;
for(int i=0;i<H;i++){
for(int j=0;j<W;j++){
if(fld[i][j])continue;
ans++;
queue<pair<int,int> >que;
que.push(make_pair(j,i));
while(!que.empty()){
int nx=que.front().first,ny=que.front().second;
que.pop();
for(int i=0;i<4;i++){
int tx=nx+dx[i],ty=ny+dy[i];
if(tx<0 || W<tx || ty<0 || H<ty || fld[ty][tx]>0)continue;
que.push(make_pair(tx,ty));
fld[ty][tx]=1;
}
}
}
}
return ans;
}
int main(void){
while(cin >> W >> H,W|H){
cin >> N;
for(int i=0;i<N;i++)
cin >> X1[i] >> Y1[i] >> X2[i] >> Y2[i];
fill(fld[0],fld[2002],0);
W=compress(X1,X2,W);
H=compress(Y1,Y2,H);
for(int i=0;i<N;i++){
fld[Y1[i]][X1[i]]++;
fld[Y1[i]][X2[i]]--;
fld[Y2[i]][X1[i]]--;
fld[Y2[i]][X2[i]]++;
}
for(int i=0;i<H;i++){
for(int j=1;j<W;j++){
fld[i][j]+=fld[i][j-1];
}
}
for(int i=1;i<H;i++){
for(int j=0;j<W;j++){
fld[i][j]+=fld[i-1][j];
}
}
cout << bfs() << endl;
}
return 0;
}


